双链Su-Schrieffer-Heeger模型的纠缠陈数
王茂,李志坚
(山西大学 理论物理研究所,山西 太原 030006)
0 引言
虽然拓扑是源于数学的一个概念,但由于一些物理系统的能带结构具有拓扑结构,而且系统的能带结构决定着系统的物理性质,因此,对物理体系的拓扑特性的研究成为了近年来比较热门的课题[1]。从拓扑的角度对物质进行分类是当前理解物质相变的一种基本思想[2]。根据物理体系所具有的对称性,已经对无相互作用物理系统的拓扑相进行了不同的分类[3],不同类型的拓扑相又可以用不同的方法或不同的拓扑不变量来表征。比如量子霍尔态可以用称为陈数的一个整数来表征[4],具有时间反演对称性的拓扑绝缘体可以用Z2拓扑不变量表征等。量子霍尔效应、量子自旋霍尔效应以及拓扑绝缘体等这些新奇的物理效应都是由于物理体系的拓扑特性所致[5]。一个具有体能隙的绝缘体,在它的非平庸拓扑相会出现无带隙的边缘态[6],这为开发新的物理器件提供了一种途径[7-9]。
量子纠缠是量子力学中的一个基本概念,在经典物理中没有对应的量,通过纠缠熵的变化可以描述量子系统的量子相变[10]。拓扑纠缠熵是表征分数量子霍尔态的一个重要指标,通过它可以识别出分数量子霍尔态[11]。人们也应用子系统之间的量子纠缠来研究拓扑绝缘体,子系统的划分不仅仅局限在位置空间上的划分,可以是更广义的划分[12-13]。一个系统可以被人为地分为两个子系统,约化密度矩阵的纠缠谱预示了在划分边界处存在着边界态[14],本文中,我们研究双链SSH模型的拓扑特性[15],把每一条链作为一个子系统,总系统的关联函数投影到一个子系统上,根据关联函数和哈密顿量的关系,定义出子系统的纠缠哈密顿量,通过纠缠哈密顿量的本征函数计算子系统的贝里相位,从而得到纠缠陈数[16]。文献[16]在研究Rice-Mele链梯模型时,得到的每条链的纠缠陈数不同,本文研究的双链SSH模型得到的每条链的纠缠陈数相等,其与系统的能带结构反映的拓扑特性完全一致,由此用一条链的纠缠陈数就可以作为拓扑不变量来描述系统的拓扑特性。
1 双链SSH模型及纠缠陈数
本文通过计算纠缠陈数研究由两条二聚化链组成的链条型双链SSH模型的拓扑特性。每条二聚化链是由晶格常数为a的一维格点线上的奇格点向左位移,偶格点向右位移形成的一个原胞内包含两个原子的复合链条。把奇数格点处的原子记作A,偶数格点处的原子记作B,由A和B组成的二聚化链中的原胞用n计数,则单条二聚化链的哈密顿量为

(1)
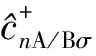
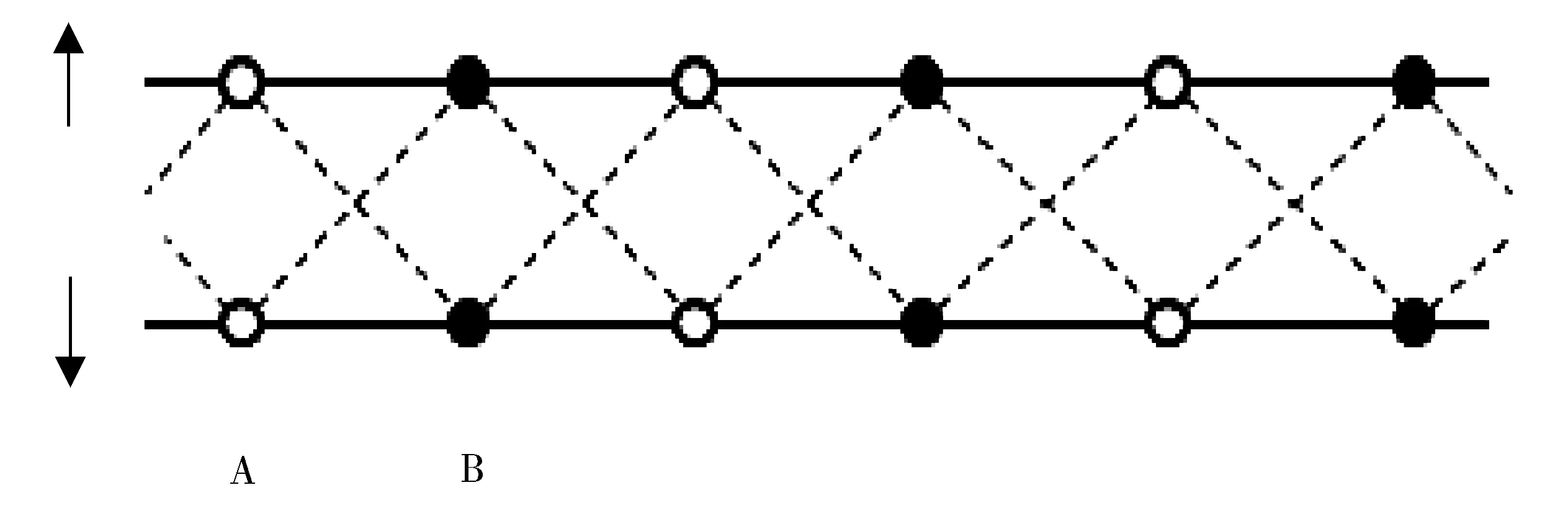
Fig.1 Diagrammatic sketch of double chain SSH model,using ↑ to mark the upper chain and ↓ to mark lower.The atom A is indicated by a hollow point, the atom B is a solid point,and the coupling between the upper and lower chains is illustrated by a broken line图1 双链SSH模型的示意图上链用↑标记,下链用↓标记,空心点表示A原子,实点表示B原子,虚线表示上链和下链之间的耦合
考虑↑链和↓链之间的相邻A、B原子之间的相互跃迁作用,而不考虑同种原子之间的跃迁作用,如图1所示,两条链之间原子相互跃迁的哈密顿量为

(2)
两条链的总哈密顿量为
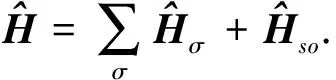
(3)
作傅里叶变换,从位置格点空间转换到k空间,格点α=A,B处原子的产生湮灭算符可表示为

(4)
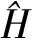

(5)

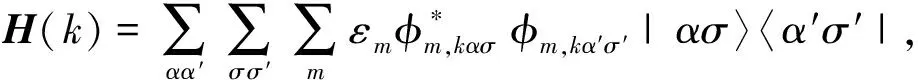
(6)
一个多体或多自由度哈密顿量可以看成由不同的子系统构成,在此,我们把双链SSH模型分为↑链和↓链两个子系统,由于两条链之间有耦合,两个子系统的量子态相互纠缠,本文通过两个子系统的纠缠陈数来刻画总系统的拓扑特性。对一个多体系统,引进关联函数
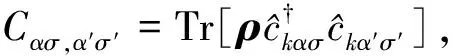
(7)
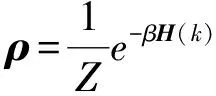
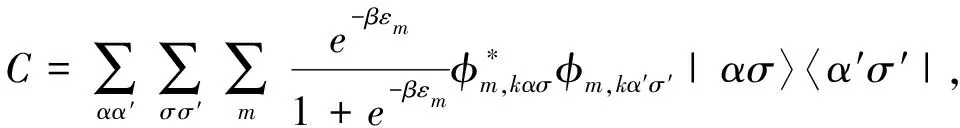
(8)
与方程(6)对比可得

(9)
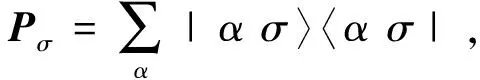
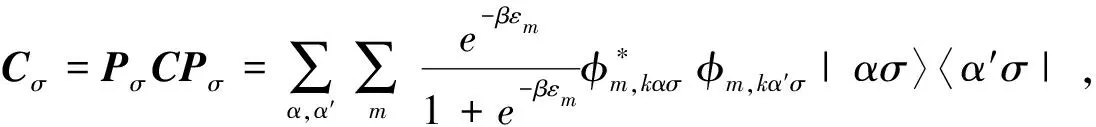
(10)
把子系统关联函数算符在A,B子格空间写为矩阵的形式有
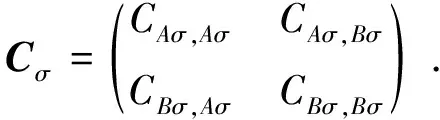
(11)
利用方程(9)的关系,由约化关联矩阵Cσ可以定义出子系统σ的哈密顿量Hσ,称之为纠缠哈密顿量。由于Hσ和Cσ有共同的本征函数,从而可以通过求解方程(11)的本征函数,并由此来计算子系统的陈数,这一陈数称为纠缠陈数。若约化关联矩阵的第l(l=1,2)个本征函数为ξlσ,相应的本征值为χlσ,即有Cσξlσ=χlσξlσ,则子系统的纠缠陈数

(12)
由于c1σ=-c2σ,因此可以选取对应较小本征值χlσ的本征函数计算纠缠陈数,并记为cσ,总系统的拓扑特性可以用(c↑,c↓)来表征。
令双链模型中同一原胞内两原子间的跃迁幅度t=w+λ,相邻原胞中A、B原子间的跃迁幅度t′=w-λ,下面我们数值地计算零温时的纠缠陈数,讨论双链SSH模型的拓扑特征随二聚化参数λ的变化情况。零温时,系统费米能之下的能级被占据,费米能之上的能级空占据,方程(10)中对系统本征指标m的求和只包含εm<0的占据部分。
2 链间耦合作用对拓扑性质的影响
当↑链和↓链间没有耦合作用,也就是系统哈密顿量中的u=ν=0时,双链模型变为孤立的两条单链,每条单链由SSH模型描述。选取w=3,纠缠陈数cσ随λ的变化情况如图2(a)所示。计算结果显示c↑=c↓,而且它们在λ=0处发生跳变;当λ<0时,c↑=c↓=-1,系统显示出非平庸拓扑特征;当λ>0时,c↑=c↓=0,系统没有拓扑特性。由纠缠陈数cσ描述的结果和单链二聚化SSH模型的拓扑结果完全相同。图2(b)给出系统能带随λ的变化,从图中可以看出,能带结构关于E=0对称。当λ=±w时,能带变为E=±2w的四个点,对称的分布于E=0周围;当λ<0时,在带隙中存在E=0的零能态,而当λ>0时,则不存在零能态。这些零能态就是拓扑保护的边缘态。
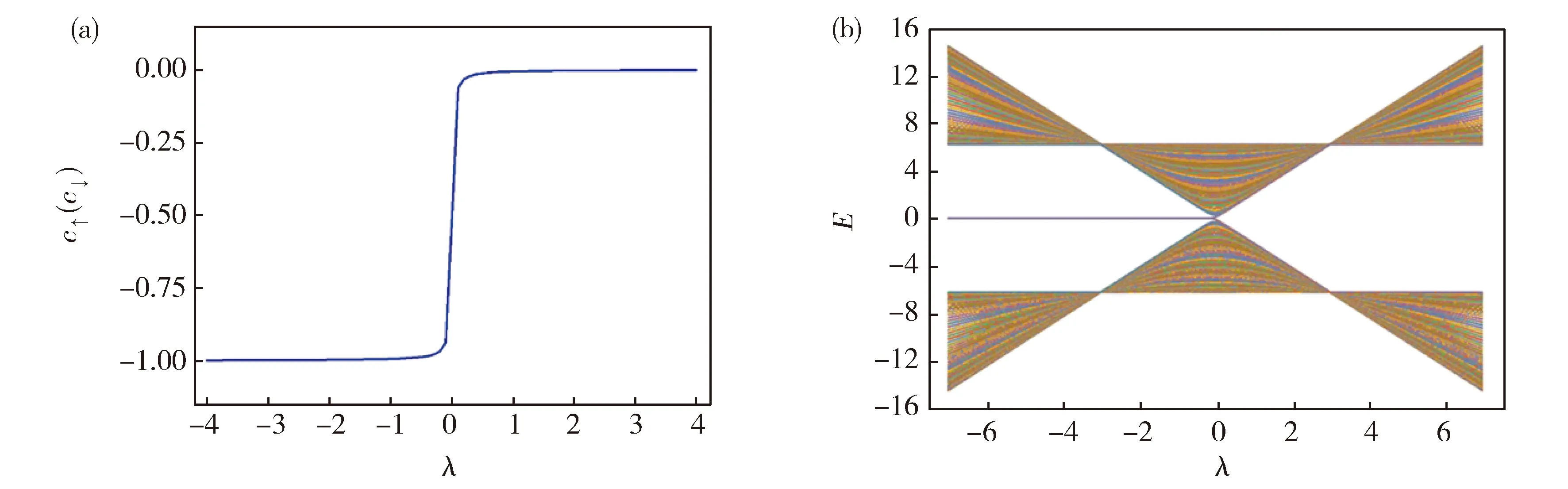
Fig.2 (a) Entanglement Chern number varies as a function of the hopping coupling;(b) Shown is the energy spectrum diagram of the system without the coupling between two chains.图2 (a)表示纠缠陈数是跃迁耦合强度的函数;(b)是两条链间没有耦合作用的能谱图
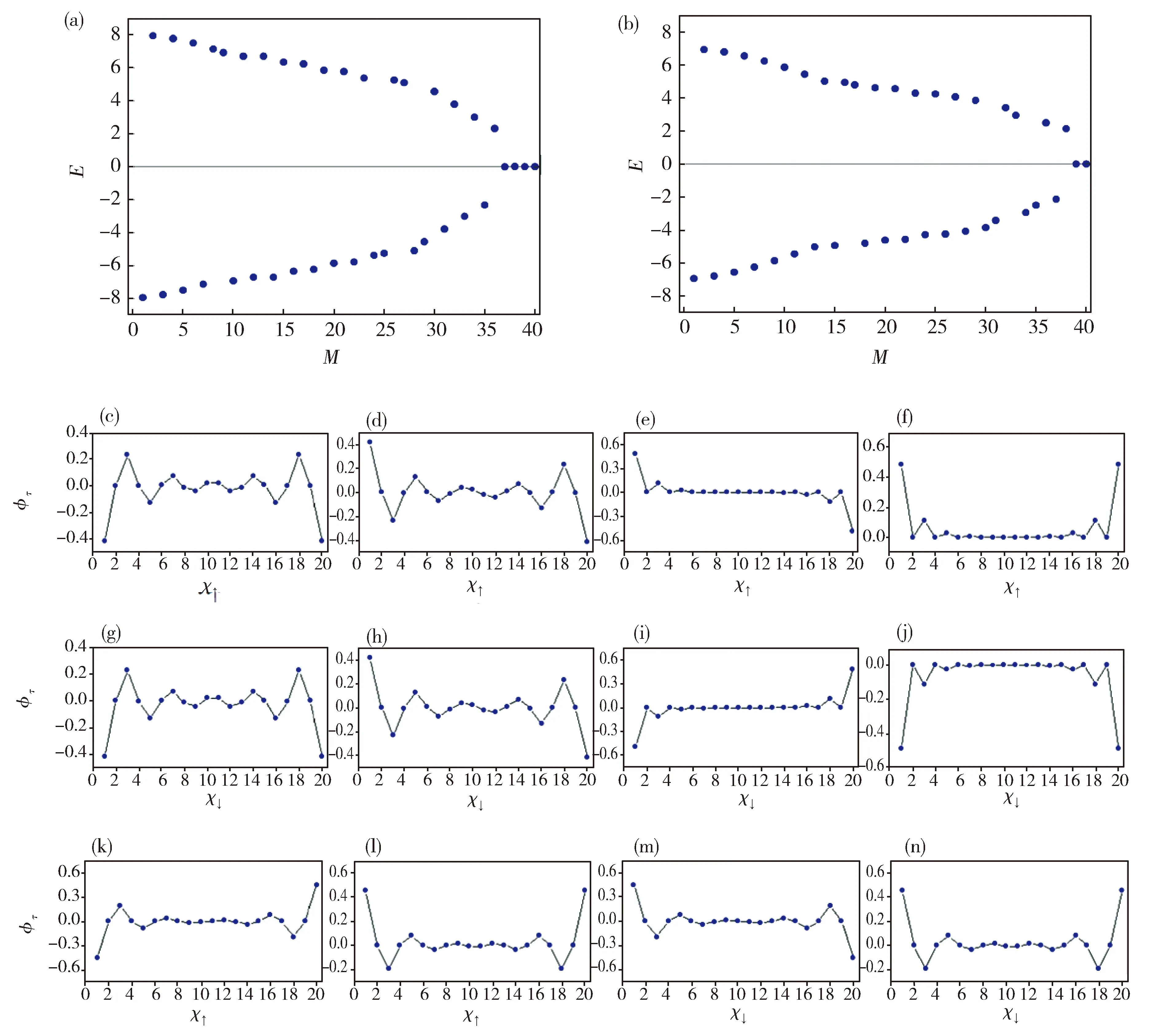
如果↑链和↓链的链间存在耦合作用,取u=2.0,v=1.0,图3(a)给出纠缠陈数随λ的变化,此种情况下仍然具有c↑=c↓,但在λ=±1.5处纠缠陈数会出现两次跳变,由-1变到-0.5,再由-0.5变到0,发生了两次拓扑相变。对比图3(b)所示的系统能带结构随λ变化的能谱图,可以看出系统的能带在λ=±1.5处发生能隙闭合。当λ<1.5时能隙中存在零能态。由于链间耦合作用的加入,使得系统能带发生劈裂,图2(b)中的一部分能级会向左平移,另一部分则向右平移,平移的大小为λ=(u+v)/2。能级在左右平移的过程中,能带的宽度也会发生改变。当u>v时,向左平移的能带宽度会变宽,而向右平移的能带宽度会变窄。而当u Fig.3 (a) Variation of entanglement Chern number c↓(c↓) with the hopping coupling λ;(b) The energy spectrum diagram of the system considering the coupling between two chains.图3 图(a)给出了纠缠陈数c↑(c↓)随跃迁耦合强度的变化;(b)是考虑两条链间的耦合作用时系统的能谱图 除了纠缠陈数的大小不同之外,为了进一步分析λ<-1.5和-1.5<λ<1.5两个范围内非平庸拓扑特性的差异,我们分别在每个范围内取λ=-2.5和λ=0.5,给出↑链和↓链中各包含10个原胞的有限长双链,即总格点数N=40时的能级图,如图4(a)和(b)所示,图中横坐标M表示能级计数指标。从图4(a)中可以发现,当λ=-2.5时,零能级是四重简并的;如图4(b)所示,当λ=0.5时,零能级发生的是二重简并。如果零能量简并的能级用Eτ表示,与之相对应的各本征态分别记为|φτ〉,其中τ为零能级计数指标。图4(c-j)和图4(k-n)分别给出λ=-2.5和λ=0.5两种取值情况下,各零能本征态在格点位置上的分布概率幅,图中横坐标x↑和x↓分别表示↑链和↓链的格点位置。其中,当能级在发生四重简并时,图4(c)和(g)、(d)和(h)、(e)和(i)、(f)和(j)中的φτ分别取φ1、φ2、φ3和φ4;而当能级在发生二重简并时,图4(k)和(m)、(l)和(n) 中的φτ分别取φ1和φ2。从图中可以发现,这些本征态在各格点位置上的分布概率幅呈奇宇称或偶宇称结构,并且在有限长格点线的边缘处分布概率最大,正是拓扑保护的边缘态。 Fig.4 Energy spectrum for λ=-2.5 (a) and λ=0.5 (b), respectively;The probability distribution at the lattice position for eigen states with zeroenergy for λ=-2.5 (c-j) and λ=0.5 (k-n), respectively.图4 图(a)和(b)分别表示在λ=-2.5和λ=0.5时的能谱图。图(c-j)和(k-n)分别表示在λ=-2.5和λ=0.5时零能本征态在格点位置上的分布概率幅 由于约化关联函数和纠缠哈密顿量有着相同的本征函数,通过约化关联函数来替代纠缠哈密顿量求得本征波函数,并定义纠缠陈数。本文通过纠缠陈数研究了双链SSH模型的拓扑特性。在研究的模型中,把每条链作为子系统,发现每条链的纠缠陈数相等,而且总系统的拓扑特性可以通过子系统的纠缠陈数来表征。对比无链间耦合作用和有链间耦合作用的两种情况,通过纠缠陈数发现,链间的耦合会使得系统的拓扑特性随着相邻格点间的跃迁参数的变化会发生两次转变。结合系统的能谱图,能带结构中能隙的闭合点和纠缠陈数的跳变点相同,说明约化子系统的纠缠陈数能够很好地描述复合系统的拓扑特征,在复合系统的非平庸拓扑区域,存在不同简并度的零能束缚态,这些本征态正是受拓扑保护的边缘态。因此,模型中两条链之间的耦合作用的加入会使得系统的拓扑相图更加丰富。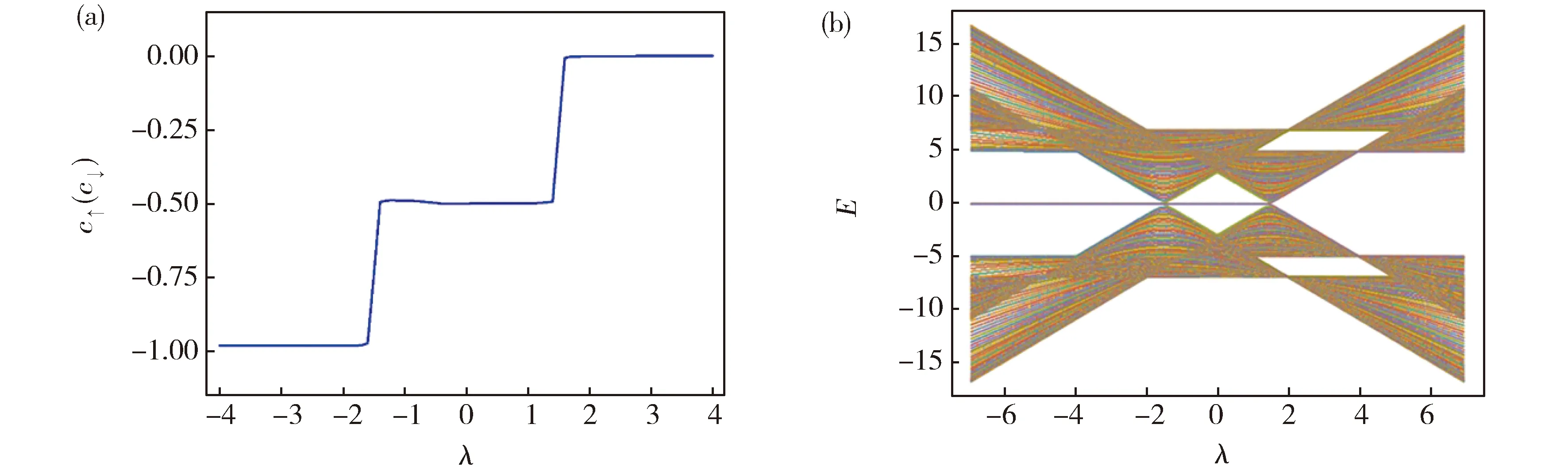
3 结论

