不同度量下集成属性选择器的对比研究

亓慧，史颖

(太原师范学院 计算机科学与技术系,山西 太原 030619)

0 引言

在粗糙集理论[1-2]的研究发展过程中,属性约简因其在行为分析、图像处理、推荐系统等各种实际问题中的应用性,受到了众多学者的关注[3-6]。经过深入的分析,在涉及属性约简的具体实现问题时,基于适应度函数的方法[7]因其时间高效性而备受青睐,其过程可以大致归纳为:给定一个适应度函数,通过该函数评估各个候选属性的重要度,依次选出最重要的属性,直到选出的属性满足预设的约束条件为止。

然而,大多数利用适应度函数法求取约简的研究工作往往只构建或使用单一的适应度函数,该策略并不能有效应对实际应用中的各种复杂问题,譬如,当面对类别不平衡数据时,单一的适应度函数在整个数据中笼统地评估属性的重要度,武断而直接,并没有深度挖掘属性在各个类别当中重要度的差异性,容易导致属性在小类下重要度被淹没的情况;当面对数据扰动问题时,利用单一的适应度函数所求得的约简往往不够全面,无法满足多层次、多视角以及多粒度[8-10]的需求。

为了解决该问题,Yang和Yao[11]设计了一种集成属性选择器。不同于以往的属性约简方法,该选择器通过构建多个适应度函数,在每一轮迭代选择中,利用这些适应度函数,对同一候选属性进行多次评估,继而综合多次评估结果,采取集成投票的机制,选出此次迭代中最重要的属性。充足的实验表明,该机制有利于在数据扰动、粒度变化等环境下,提升约简结果以及其相关分类结果的稳定性。在此研究工作的基础上,Liu等人[12]将集成属性选择器应用于半监督特征选择问题中去,显著地提升了由约简所得的分类准确率;Wang等人[13]将其推广至在线特征选择的问题,在提升由约简所得分类准确率的同时,还有效地降低了求取约简所需的时间消耗。需要注意的是,不同的度量可以构建不同的适应度函数,其相应的集成属性选择器的性能亦会有所差异。为了分析这种差异,本文借助邻域粗糙集模型[14],并分别将局部近似质量[11]、局部条件熵[13]以及局部邻域决策错误率[12]引入到集成属性选择器中,对其约简结果进行了实验对比分析。

1 基本知识

1.1 邻域粗糙集

在粗糙集理论中,一个决策系统可以表示为二元组DS=,其中U是一个非空有限的样本集合,亦被称作论域;AT是非空有限的条件属性集合;d是决策属性。此外,∀x∈U,d(x)表示样本x的决策属性值,即类别标签。

根据决策属性d,∀A⊆AT,可以定义属性集合A上的一个不可分辨关系为

IND({d})={(x,y)∈U2:d(x)=d(y)} .

(1)

根据此不可分辨关系,可以进一步得到论域U上的一个划分为

U/IND({d})={X1,X2,…,Xq}.

(2)

∀Xi∈U/IND({d})被称之为第i个决策类,特别地,用[x]d来表示包含样本x的决策类。

定义1[14]给定一个决策系统DS,非负的邻域半径δ,∀A⊆AT,DS中的邻域关系可被定义为

δA={(x,y)∈U2:ΔA(x,y)≤δ},

(3)

其中ΔA(x,y)表示样本x与y关于属性集合A的距离。

相应地,∀x∈U,其关于属性集合A的邻域为

δA(x)={y∈U:ΔA(x,y)≤δ}.

(4)

定义2[14]给定一个决策系统DS,∀A⊆AT,∀Xi∈U/IND({d}),Xi关于A的下近似与上近似就可分别定义为

(5)

(6)

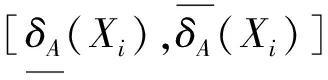
定义3[1]给定一个决策系统DS,∀A⊆AT,关于A的近似质量可定义为

(7)

其中|X|表示集合X的基数。

定义4[15]给定一个决策系统DS,∀A⊆AT,关于A的条件熵可定义为

(8)

定义5[14]给定一个决策系统DS,∀A⊆AT,关于A的邻域决策错误率可定义为

(9)

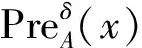
1.2 属性约简

属性约简[15-17]是粗糙集理论中的核心研究内容之一。当需求发生变化,属性约简的定义也会有所不同,以度量近似质量与条件熵为例,近似质量约简[1]的定义为能够保持或提升近似质量的最小属性子集,而条件熵约简[15]的定义则是能够保持或者降低条件熵的最小属性子集。鉴于此,通过归纳总结众多属性约简的共性,Yao等人[7]给出了属性约简一般形式的定义,具体定义如下所示。

定义6[7]给定一个决策系统DS,∀R⊆AT,ρ为预设的约束条件,R可被视作一个约简当且仅当

(1)R满足约束条件ρ;

(2) ∀R′⊂R,R′不满足约束条件ρ。

需要注意的是,给定不同的度量,定义6中的预设约束条件ρ可以有多种不同的形式:当选取近似质量为度量时,为了尽可能地提升近似质量,ρ一般设置为“γ(A)≥γ(AT)”;当选取条件熵为度量时,为了尽可能地降低条件熵,ρ一般设置为“ε(A)≤ε(AT)”;当选取邻域决策错误率为度量时,为了尽可能地降低邻域决策错误率,ρ一般设置为“η(A)≤η(AT)”。

根据定义6,通过引入启发式算法,可以给出如算法1所示的求解约简算法。

算法1 单一适应度函数的求解约简算法 输入: 决策系统DS,约束条件ρ,适应度函数φ. 输出: 约简R. 步骤1 R←ø; Repeat步骤2 (1) ∀a∈AT-R,计算其属性重要度φ(a);(2) 选择属性b满足φ(b)=max{φ(a):∀a∈AT-R};(3) R←R∪{b};Until R满足约束条件ρ 步骤3 输出R.

一般而言,算法1中适应度函数通过计算加入属性前后的度量值变化来反映候选属性的重要度,每次迭代都会选出重要度最大的属性,直到选出的属性满足约束条件为止。考虑到度量的性质不同,适应度函数的计算也会有所区别,譬如,近似质量提升得越大,属性则越重要,此时构建适应度函数为φ(a)=γ(A∪{a})-γ(A);而条件熵与邻域决策错误率降低得越大,属性越重要,可分别构建适应度函数为φ(a)=ε(A)-ε(A∪{a})与φ(a)=η(A)-η(A∪{a})。

2 集成属性选择器

算法1通过构建单一的适应度函数求解约简,此类方法对于属性评估与选择的机制过于单一武断,没有充分权衡每个属性在不同视角下的重要度。譬如,在某次迭代中,某个属性在单一的适应度函数评估下被认为是重要的,但当数据发生轻微扰动,造成粒度的变化时,该属性极有可能就不再重要,最终就容易造成约简具备较差的泛化性能。鉴于此,Yang和Yao[11]设计了一种集成属性选择器,其具体方法如算法2所示。

如算法2所示,多个适应度函数是集成属性选择器明显区别于算法1的关键部分。不言而喻,如何构建多个适应度函数就成为了集成属性选择器中的核心问题。事实上,适应度函数通常根据度量来构建,那么多个度量就可构建多个适应度函数。就目前而言,较为合理的方法是根据局部度量来构建同质型的适应度函数,常见的局部度量有局部近似质量[18],局部条件熵[13]与局部邻域错误率[12]。

以下就给出这三种局部度量的具体定义。

定义7[11]给定一个决策系统DS,∀A⊆AT,A关于决策类Xi的局部近似质量可定义为

(10)

定义8[13]给定一个决策系统DS,∀A⊆AT,A关于决策类Xi的局部条件熵可定义为

(11)

定义9[12]给定一个决策系统DS,∀A⊆AT,A关于决策类Xi的局部邻域决策错误率可定义为

(12)

根据定义6-8所示的局部度量,不难构造相应的适应度函数,即φi(a)=γ(A∪{a},Xi)-γ(A,Xi),φi(a)=ε(A,Xi)-ε(A∪{a},Xi)以及φi(a)=η(A,Xi)-η(A∪{a},Xi)。显然,不同于1.2节所介绍的适应度函数,此时构造的适应度函数不再单一,其数目等同于样本中决策类的数目,考虑到现实数据一般具有二类甚至是多类,多个适应度函数就可以轻而易举地实现。

3 实验对比

文献[11-13]已经分别对由不同局部度量构建的集成属性选择器与算法1进行了比较,本文就不再加以赘述。然而,考虑到局部度量的选择不同,集成属性选择器的性能也会有所差异,孰优孰劣还有待进一步地分析,故本文就此问题开展了实验对比工作。

3.1 数据集

本次实验选取了6组UCI标准数据集,其基本信息如表1所示。

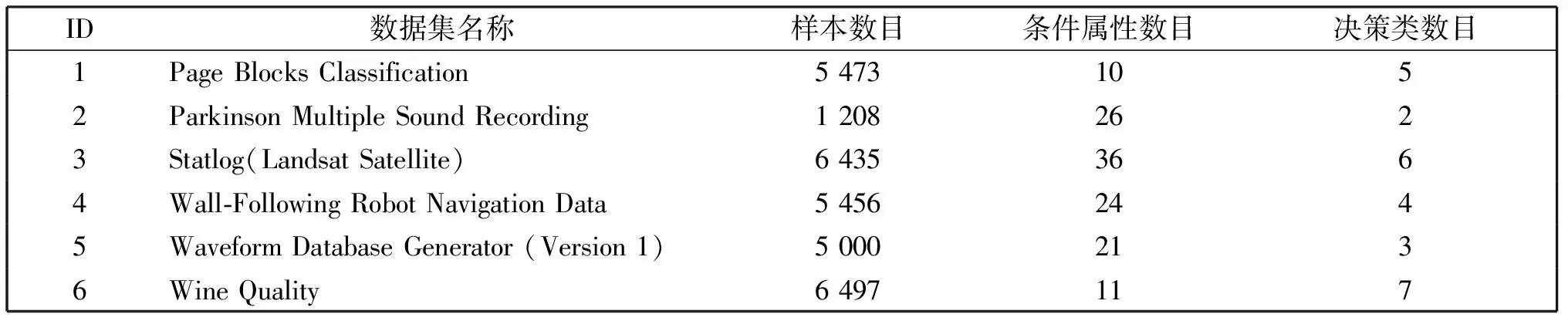
表1 实验数据集描述

3.2 实验设置

本次实验的环境为PC机,Windows 10操作系统,双核2.60 GHz CPU,16.0 GB内存,Matlab R2014a实验平台。

此外,实验采用了5折交叉验证的方法,即将实验数据集随机平均分为5份,每次取其中4份作为训练样本,剩余1份作为测试样本。实验还选取了10个半径δ,值分别为0.03,0.06,…,0.3。在每个半径下,利用算法2所示的集成属性选择器分别在每份训练样本上求取局部近似质量约简,局部条件熵约简以及局域邻域决策错误率约简。最后主要对比选取不同半径时,在5折交叉验证下由约简在测试样本上所得的平均分类准确率。

3.3 实验结果

本次实验选取了两种分类器,即CART分类器与KNN分类器来对比不同度量下集成属性选择器求得约简产生的分类准确率,其具体结果如图1所示。

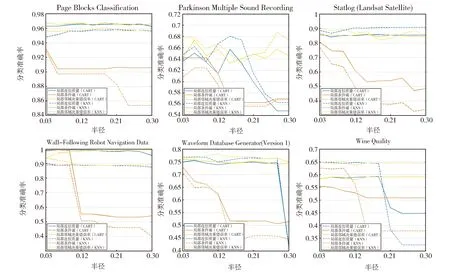
Fig.1 Comparison among classification accuracies derived by reducts图1 由约简所得分类准确率的对比

通过观察图1,可以得到以下结论。

(1) 不管采用CART分类器还是KNN分类器,相比于局部近似质量与局部条件熵,由局部邻域决策错误率构建的集成属性选择器求得的约简能够提供更好的分类性能,譬如,在数据集Waveform Database Generator (Version 1)上,由局部邻域决策错误率约简所得的分类准确率可以稳定在0.75以上,而由局部条件熵约简所得到的分类准确率就一直低于0.75,甚至当半径处于0.21至0.30时,分类准确率已不足0.55,由局部近似质量约简所得的分类准确率则在半径为0.30时陡降至0.45以下;

(2) 对于局部条件熵下的集成属性选择器而言,采用CART分类器能够使所选取的约简提供更好的分类效果,而对于局部近似质量与局部邻域决策错误率下的集成属性选择器而言,采用CART分类器与KNN分类器则各有优劣,譬如,在数据集Page Blocks Classification与Wall-Following Robot Navigation Data上,采用CART分类器能够使相应的约简产生更高的分类准确率,但在数据集Statlog(Landsat Satellite)与Wine Quality上,情况就有所不同,显然是采用KNN分类器能够使约简产生更好的分类结果。

4 结论与展望

集成属性选择器已经被成功地应用于半监督学习、在线学习等问题中,为探索不同度量下集成属性选择器的性能差异,本文借助邻域粗糙集,选取了3种常用的局部度量,即局部近似质量、局部条件熵以及局部邻域决策错误率,分别构建了不同的集成属性选择器,并对其约简结果进行了对比分析。实验结果表明,当选择局部邻域决策错误率作为度量时,集成属性选择器所产生的约简能够提供更高的分类准确率。

在该对比工作的基础上,下一步将讨论集成属性选择器在其他粗糙集模型下的性能差异,同时亦可考虑集成属性选择器在多粒度环境下的加速或优化,以扩展该选择器的应用范围。