发动机空气弹簧液压悬置动态特性及参数灵敏度研究

侯锁军，杨 慰

(1.河南工学院 车辆与交通工程学院，河南 新乡 453000；2.中国汽车技术研究中心有限公司，天津 300300；3.东风商用车技术中心，武汉 430056)

随着消费者对汽车乘坐舒适性要求的提高以及汽车市场产品竞争日益激烈，良好的汽车NVH特性正逐渐成为汽车产品竞争力的核心之一。然而汽车发动机大功率化和轻量化使得动力总成的振动激励不断加剧，这就对动力总成悬置系统的隔振特性提出了更高的要求，并希望其能满足车辆使用过程中任何工况的需要[1-3]。

发动机悬置作为发动机的隔振元件，经历了橡胶悬置、被动式液压悬置和半主动/主动液压悬置的发展历程[4-5]。橡胶悬置和被动式液压悬置结构确定以后表征其动态特性的两个参数动刚度和阻尼角是不可调的[6-9]，不能满足汽车复杂工况对悬置动特性的要求。主动液压悬置由于其结构和控制策略复杂，应用较少。半主动悬置结构和控制策略简单，成本低，应用前景良好。其中空气弹簧式半主动液压悬置(以下简称空气弹簧液压悬置)是一种新型的、隔振性能良好的发动机隔振元件，其利用电磁阀控制悬置内部空气腔的开闭改变悬置的动刚度和阻尼角，相对于其他类型半主动液压悬置其动刚度和阻尼角变化范围大，满足了汽车发动机在不同工况下的对悬置隔振的要求。

Azadi等[10]设计了一种刚度可变的半主动悬置，通过调节压电作动器和开关型控制器来改变可变刚度弹簧的预应刚度，使半主动控制悬置产生极大的动刚度特性，并且能耗很低。国内研究方面，贺良勇[11]对空气弹簧液压悬置进行了动特性分析研究。范让林等[12]对解耦膜刚度可变的空气弹簧液压悬置进行了动特性分析研究。

通过分析空气弹簧液压悬置国内外研究现状可见，对新型的发动机空气弹簧液压悬置的动特性研究还不够深入，且较少有人对空气弹簧液压悬置动特性的影响因素进行灵敏度分析。本文设计了一款新型的空气弹簧液压悬置，其主要特点是在其他类型半主动液压悬置的基础上，加入了空气弹簧结构。采用了上液室等效体积刚度替代解耦膜以及密闭空气腔对悬置动特性的影响，基于流体力学相关理论建立了空气弹簧液压悬置力学模型，并通过试验验证了该模型的正确性，分析了空气腔开启和关闭时空气弹簧的动态特性；采用该模型研究了空气弹簧液压悬置模型参数对悬置动刚度的影响，获得了这些参数对空气弹簧液压悬置动刚度影响的灵敏度。

1 空气弹簧液压悬置结构与工作原理

1.1 空气弹簧液压悬置结构

本文所设计的空气弹簧液压悬置结构示意图如图1所示，主要包括：橡胶主簧、上液室、下液室、电磁阀、隔板、惯性通道、解耦膜、空气腔、橡胶底膜。

1-连接动力总成的螺栓孔；2-连接车架的螺栓孔；3-金属外壳；4-橡胶底膜；5-下液室；6-电磁阀；7-空气腔；8-解耦膜；9-惯性通道；10-隔板；11-上液室；12-橡胶主簧
图1 空气弹簧液压悬置的结构示意图
Fig.1 Schematic diagram of air spring hydraulic mount

其中空气腔是由解耦膜与隔板凹槽合围形成的腔体，该空气腔体通过一个小孔与外界大气相通，但当电磁阀通电堵住小孔口时，则是密闭的空气腔体，形成类似空气弹簧。

1.2 空气弹簧液压悬置工作原理

空气弹簧式液压悬置工作时，上螺栓受动力总成激励产生振动，带动橡胶主簧对上液室作类似活塞泵吸的运动，于是上液室的体积连续地发生增大和缩小的变化，液体通过惯性通道在上下液室间来回流动，以适应上液室体积的变化。由于惯性通道壁和流动液体间的相互黏滞阻性，液体连续快速地通过时受到惯性通道的阻力，用来吸收来自动力总成的振动能量。空气腔关闭时，自身刚度大，对橡胶主簧的作用力大，表现为悬置的动刚度大，空气腔与大气相通时，自身刚度较小，对橡胶主簧的作用力小，表现为悬置的动刚度小。

2 空气弹簧液压悬置建模

对解耦膜、空气腔以及橡胶主簧的体积刚度进行的等效合并，在建立悬置模型时，不再单独考虑解耦膜和空气腔结构，而是以一个通过理论和试验得出的等效上液室体积刚度来代替[13]。为突出影响悬置模型的主要因素，对半主动液压悬置进行如下假设[14-15]：假设空气腔内气压均匀，上、下液室内压力均匀；忽略空气腔内气体温度变化对气压造成的影响；上、下液室的体积刚度视为常量；液体为不可压缩流体。液压悬置的力学模型如图2所示。

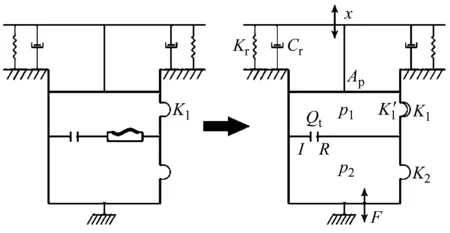
Ap-橡胶主簧泵吸液体的等效活塞面积;Kr、Cr-橡胶主簧的动刚度和阻尼系数；K1、K2-上液室和下液室的体积刚度；p1、p2-上液室和下液室的压力；Qt-惯性通道内的液体流量；I、R-惯性通道内液体的惯性系数和流量阻尼系数；x、F-主簧振动位移和悬置的传递力
图2 解耦膜与空气腔等效合并后的悬置模型示意图
Fig.2 Schematic diagram of the mount model after the equivalent combination of the decoupling membrane and the air chamber

由于解耦膜与橡胶主簧的体积刚度被等效合并，对于上液室的液体，可以建立液体流动的连续性方程[16-17]

(1)

与传统的解耦膜式液压悬置不同，本文设计的空气弹簧液压悬置的下液室液体并不与解耦膜/解耦盘下表面接触，因此对于下液室的液体，可建立液体流动的连续性方程

(2)

对于惯性通道内的液体，液压差与其受到的惯性力与阻尼力平衡，可以建立该部分液体流动的连续性方程

(3)

取整个系统作为研究对象，传递到车架固定端的力由橡胶主簧弹性力、阻尼力和上液室液压力组成，即：

(4)

(5)

式中，U为输入量，A为系数矩阵，B为控制系数矩阵，C为输出状态系数矩阵，D为控制系数矩阵，且有

将状态方程和输出方程写成矩阵形式即为

(6)

y=F=

(7)

系统的传递函数为

(8)

其中s=jω，因此悬置的复刚度可表示为

(9)

式中，ω为角频率，它可通过ω=2πf转换为频率。

对复刚度矩阵形式进行转换和简化，可以得到其表达式为

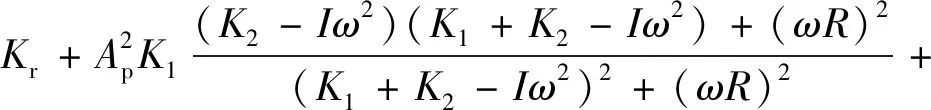
(10)

按照美国汽车工程学会修订的《Testing Dynamic Properties of Elastomeric Isolators》中的定义，悬置的存储刚度为复刚度的实部，阻尼角为复刚度虚部与实况比值的反正切值，即：

Kd=real(K*)

(11)

(12)

3 空气弹簧液压悬置动特性研究

试验设备为美国的MTS831试验台，如图3所示。试验时，由试验台控制计算机的信号发生器产生所设定频率和振幅的正弦信号，经放大后加到作动器上，作动器下端固定，上端作动，上端的位移传感器和力传感器将信号传递给试验台的测试软件，有测试软件计算出悬置的动刚度和阻尼角的频变特性曲线，其原理如图4所示。测试样件的内部结构如图5所示。本文主要研究悬置的低频垂向振动控制，测试Z向如图6所示，作动器激励频率为0～50 Hz，悬置施加1 000 N的预载，振幅为1 mm。试验过程中重复三次，取平均值。

图3 试验设备Fig.3 Test equipment

图4 测试原理Fig.4 Test principle

该空气弹簧悬置各个参数值如表1所示，将参数代入式(10)、(11)、(12)进行理论仿真，对该空气弹簧液压悬置的动刚度和阻尼角进行台架试验后，将空气弹簧液压悬置的动刚度和阻尼角仿真值与试验值进行对比，结果如图7～图10所示。

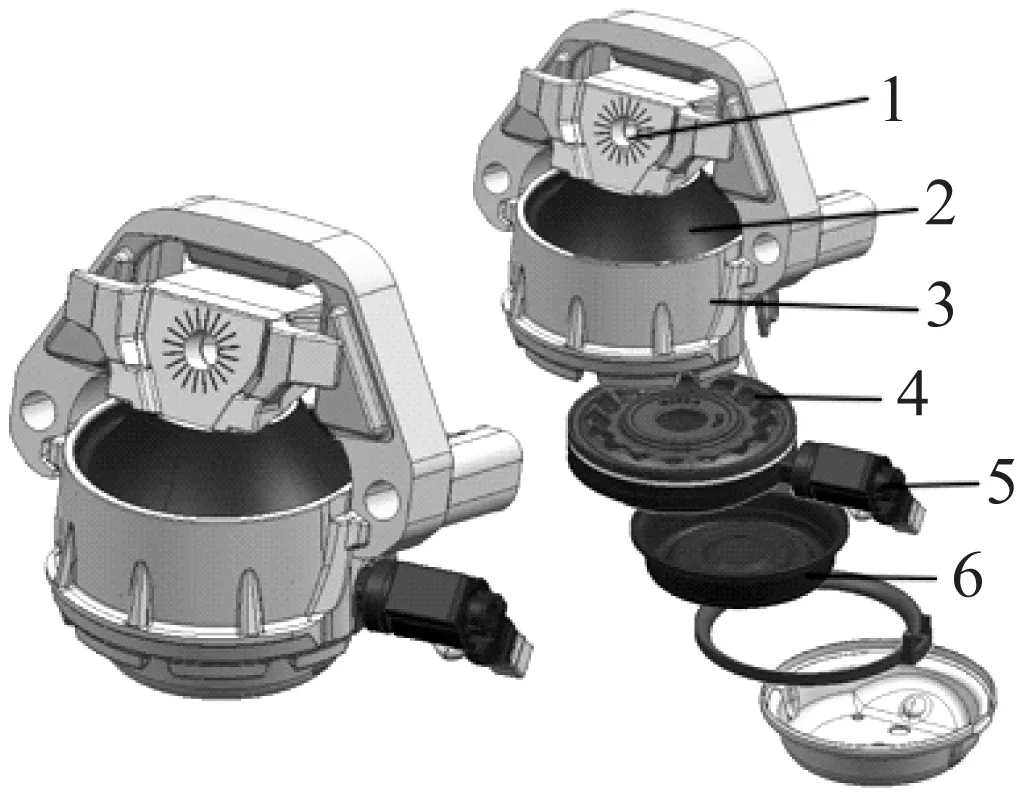
1-动力总成端连接螺栓孔；2-橡胶主簧；3-金属外壳；4-解耦盘总成；5-电磁阀；6-橡胶底膜
图5 空气弹簧液压悬置结构
Fig.5 Structure of air spring hydraulic mount

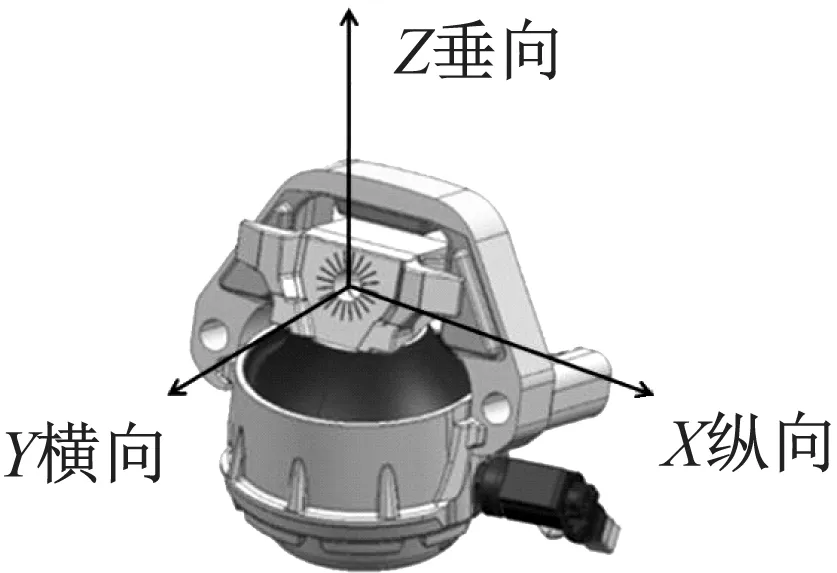
图6 悬置三向示意图Fig.6 Mount three-way diagram

表1 模型仿真参数
Tab.1 Model simulation parameters

参数数值橡胶主簧动刚度/(N·m-1)1.8×105橡胶主簧阻尼系数/(N·s·m-1)1.0×102橡胶主簧的等效活塞面积/m22.7×10-3空气腔闭上液室等效体积刚度/(N·m-5)2×1010下液室体积刚度/(N·m-5)5×108惯性通道液体的质量惯性系数/(kg·m-4)2.5×106惯性通道液体的流量阻尼系数/(N·s·m-5)1.0×108

图7 空气腔关闭悬置动刚度对比Fig.7 Comparison of mount dynamic stiffness with the closed air chamber

有对比曲线可以看出，动刚度和阻尼角理论仿真与试验曲线趋势基本一致，在空气腔关闭时，空气弹簧悬置表现出大刚度大阻尼特性，动刚度达到最大值480 N/mm，阻尼角最大值62°，当空气腔开启时，空气弹簧悬置表现出小刚度小阻尼特性，动刚度最大值仅有300 N/mm，阻尼角最大值仅有30°。比较空气腔开启和空气腔关闭两种状态，动刚度增大了60%，阻尼角增大了106%，可以有效的进行发动机各种工况下的振动控制。

图8 空气腔关闭悬置阻尼角对比Fig.8 Comparison of mount damping angle with the closed air chamber

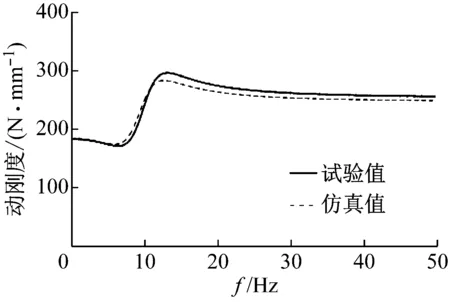
图9 空气腔开启悬置动刚度对比Fig.9 Comparison of mount dynamic stiffness with the opened air chamber

图10 空气腔开启悬置阻尼角对比Fig.10 Comparison of mount damping angle with the opened air chamber

4 模型参数灵敏度分析

在车型开发过程中，当发动机的型号及安装位置确定后，需要对悬置的动刚度和阻尼角具体数值进行优化才能达到发动机最佳的隔震性能，然后根据优化设计后的悬置动刚度和阻尼角调整悬置内部结构参数，从而达到该优化值。本文建立的悬置动力学仿真模型可较准确地表达空气弹簧液压悬置的动刚度和阻尼角，对悬置模型各参数进行调整达到其对动刚度和阻尼角的影响程度，为达到优化后的悬置动刚度和阻尼角奠定了基础。

本文在空气弹簧液压悬置各参数(如表1所示)基础上浮动±50%，研究动刚度和阻尼角的变化规律及变化百分比。

4.1 橡胶主簧动刚度和阻尼对悬置动特性的影响

橡胶主簧的动刚度对悬置的动刚度的影响非常直接，如图11、12所示，主簧动刚度在[0.9，2.7]×105N/m的范围内线性上升时，悬置的动刚度也整体随之线性上升，并且几乎不影响峰值频率。悬置的阻尼角峰值随着橡胶主簧动刚度的增大而减小，峰值频率几乎不受影响。

图11 橡胶主簧动刚度对液压悬置动刚度影响Fig.11 Influence of dynamic stiffness of rubber main spring on dynamic stiffness of hydraulic mount

图12 橡胶主簧动刚度对液压悬置阻尼角影响Fig.12 Influence of dynamic stiffness of rubber main spring on damping angle of hydraulic mount

橡胶主簧的阻尼系数在[0.5，1.5]×102N·s/m范围内的改变对悬置动刚度和阻尼角峰值和峰值频率都几乎没有影响，如图13、14所示。

图13 橡胶主簧阻尼系数对液压悬置动刚度影响Fig.13 Influence of damping coefficient of rubber main spring on dynamic stiffness of hydraulic mount

4.2 橡胶主簧等效活塞面积对悬置动特性的影响

橡胶主簧等效活塞面积变化范围为[1.35，4.05]×10-3m2，如图15、16所示。随着等效活塞面积的增大，悬置的峰值动刚度和大于18 Hz以后的动刚度大幅度地增大，但对频率小于18 Hz时悬置动刚度影响不大，对悬置峰值频率几乎没影响。橡胶主簧等效活塞面积对液压悬置阻尼角的影响主要表现在频率小于12 Hz处，随着活塞面积的增大，阻尼角峰值增大，对悬置阻尼角峰值频率影响较小。

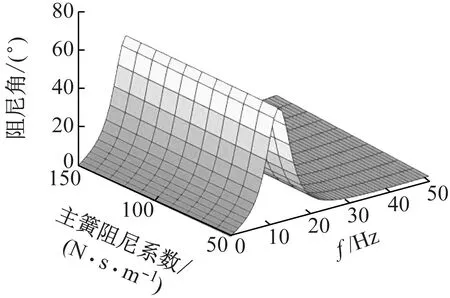
图14 橡胶主簧阻尼系数对液压悬置阻尼角影响Fig.14 Influence of damping coefficient of rubber main spring on damping angle of hydraulic mount

图15 橡胶主簧等效活塞面积对液压悬置动刚度影响Fig.15 Influence of equivalent piston area of rubber main spring on dynamic stiffness of hydraulic mount

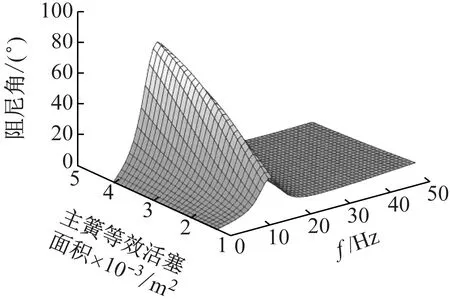
图16 橡胶主簧等效活塞面积对液压悬置阻尼角影响Fig.16 Influence of equivalent piston area of rubber main spring on damping angle of hydraulic mount

4.3 上下液室体积刚度对悬置动特性的影响

上液室的等效体积刚度对液压悬置的动刚度和阻尼角影响很大，如图17、18所示。上液室的体积刚度变化范围为[1，3]×1010N/m5，随着上液室等效体积刚度的增大，悬置动刚度和阻尼角都会大幅增大，同时还引起动刚度和阻尼角峰值频率的改变，动刚度峰值频率从13 Hz增大到20 Hz，阻尼角频率从8 Hz增大到13 Hz，这对空气弹簧液压悬置动刚度和阻尼角曲线的设计具有重要意义。

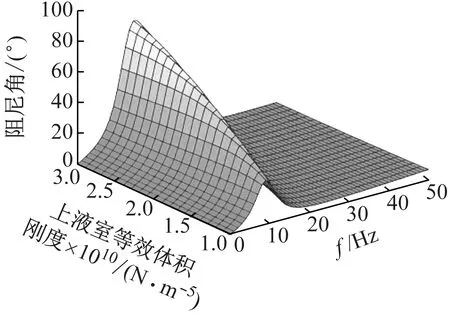
图18 上液室等效体积刚度对液压悬置阻尼角影响Fig.18 Influence of equivalent volume stiffness of upper chamber on damping angle of hydraulic mount

下液室的体积刚度在[2.5，7.5]×108N/m5范围内变化时，如图19、20所示，对液压悬置的动特性几乎没有影响。因为下液室的主要功能是容纳液体，而非力学作用，下液室体积刚度需要与上液室体积刚度拉开数量级，否则将对液压悬置动特性产生干扰。

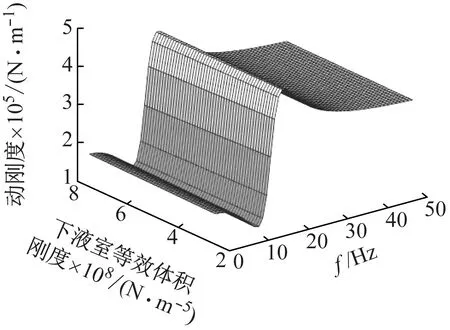
图19 下液室体积刚度对液压悬置动刚度影响Fig.19 Influence of volume stiffness of lower chamber on dynamic stiffness of hydraulic mount

4.4 惯性通道内液体特性对悬置动特性的影响

惯性通道内液体的质量惯性系数主要影响悬置的动刚度和阻尼角出现峰值的频率，即惯性系数越大，悬置的峰值频率越小，这一点可以从图21、22中动特性峰值的曲线扭曲程度和扭曲方向可以看出，当液体的质量惯性系数从1.25×106kg/m4增大到3.75×106kg/m4时，动刚度峰值频率从23 Hz提前到13 Hz，阻尼角频率从15 Hz提前到9 Hz。

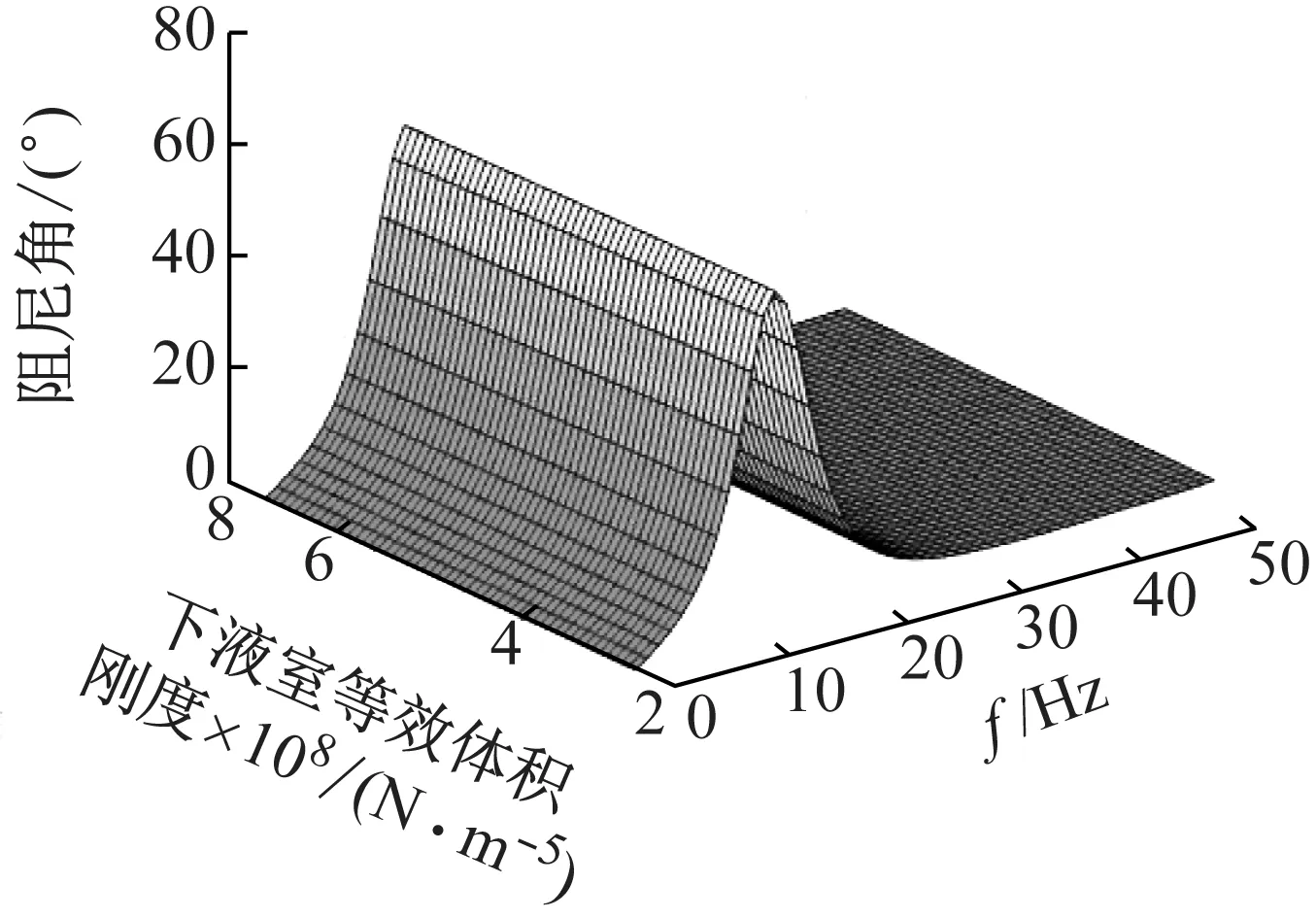
图20 下液室体积刚度对液压悬置阻尼角影响Fig.20 Influence of volume stiffness of lower chamber on damping angle of hydraulic mount

图21 惯性通道内液体惯性系数对液压悬置动刚度影响Fig.21 Influence of liquid inertia coefficient of inertia track on dynamic stiffness of hydraulic mount

图22 惯性通道内液体惯性系数对液压悬置阻尼角影响Fig.22 Influence of liquid inertia coefficient of inertia track on damping angle of hydraulic mount

惯性通道内液体的流量阻尼系数在[0.5，1.5]×108N·s/m5变化时，只对液压悬置动刚度和阻尼角的峰值大小产生影响，即流量阻尼系数越小，液压悬置的动刚度和阻尼角的峰值越大，如图23、24所示。

将空气弹簧悬置动刚度的峰值变化量ΔSi与该空气弹簧悬置原始参数(如表1所示)情况下悬置的峰值动刚度Smax的百分比，用于衡量该参数对悬置动刚度影响程度，用s1表示，表达式为

(13)

将空气弹簧悬置阻尼角的峰值变化量ΔAi与该空气弹簧悬置原始参数(如表1所示)情况下悬置的峰值阻尼角Amax的百分比，用于衡量该参数对悬置阻尼角影响的程度。用s2表示，其表达式为

图23 惯性通道内液体阻尼系数对液压悬置动刚度影响Fig.23 Influence of liquid damping coefficient in inertial channel on dynamic stiffness of hydraulic mount

图24 惯性通道内液体阻尼系数对液压悬置阻尼角影响Fig.24 Influence of liquid damping coefficient in inertial channel on damping angle of hydraulic mount

(14)

将图11～图24仿真值代入式(13)、(14)后，得出各参数对空气弹簧悬置的动刚度和阻尼角影响程度如图25、26所示。图中峰值灵敏度正值表示随着参数的增大，动刚度增大或阻尼角增大即正相关，负值表示随着参数的增大，动刚度增大或阻尼角减小即负相关。

a-橡胶主簧动刚度;b-橡胶主簧阻尼;c-橡胶主簧等效活塞面积;d-上液室体积刚度;e-下液室体积刚度;f-惯性通道内液体质量惯性系数;g-惯性通道内液体流量阻尼系数
图25 各参数对动刚度峰值灵敏度
Fig.25 Peak value sensitivity of each parameter to dynamic stiffness

由图25、26可以看出：

(1)橡胶主簧等效活塞和上液室体积刚度对悬置动刚度和阻尼角的灵敏度最大，达到76%以上，并且是正相关的关系，因此适当增大橡胶主簧等效活塞面积和上液室体积刚度有利于悬置的低频隔震。

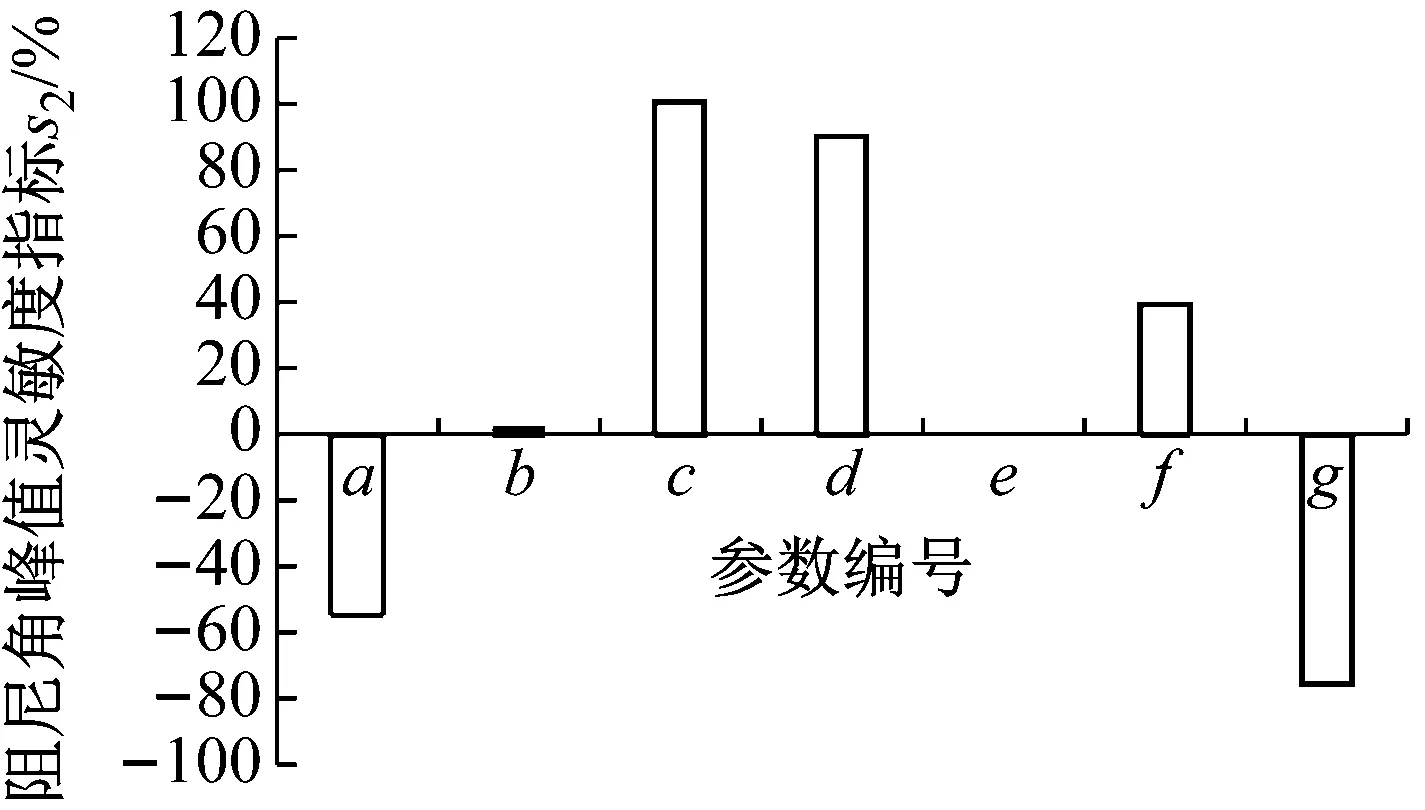
图26 各参数对阻尼角峰值灵敏度Fig.25 Peak value sensitivity of each parameter to damping angle

(2)随着橡胶主簧动刚度的增大，悬置的动刚度增大，但是悬置阻尼角减小，不利于悬置的低频隔震，因此在空气弹簧设计时橡胶主簧的动刚度不宜太大。

(3)橡胶主簧的阻尼和下液室的体积刚度对空气弹簧悬置的动刚度和阻尼角几乎没有影响，在悬置动特性设计时，可以不作为主要因素考虑。

(4)惯性通道液体质量惯性系数对空气弹簧悬置动刚度和阻尼角是正相关关系，而惯性通道内液体流量阻尼系数对空气弹簧悬置动刚度和阻尼角是负相关关系，为此适当增大惯性通道液体质量惯性系数，减小惯性通道液体流量阻尼系数有利于悬置的低频隔震。

5 结 论

(1)本文采用空气弹簧液压悬置上液室等效体积刚度替代解耦膜以及密闭空气腔对悬置动特性的影响，基于流体力学相关理论建立的空气弹簧液压悬置力学模型，通过试验验证表明该模型可以较好的反映空气弹簧液压悬置的动态特性。

(2)空气弹簧液压悬置的动刚度和阻尼角在空气腔开闭两种状态下，其变化范围较大，在空气腔关闭时，空气弹簧悬置表现出大刚度大阻尼特性，动刚度达到最大值480 N/mm，阻尼角最大值62°，当空气腔开启时，空气弹簧悬置表现出小刚度小阻尼特性，动刚度最大值仅有300 N/mm，阻尼角最大值仅有30°。比较空气腔开启和空气腔关闭两种状态，动刚度增大了60%，阻尼角增大了106%，可以有效的进行发动机各种工况下的振动控制。

(3)基于该模型对影响空气弹簧液压悬置动特性主要参数进行了灵敏度分析，得到了各参数与动刚度和阻尼角的变化关系，为空气弹簧液压悬置动特性优化设计提供了参考。