负泊松比蜂窝空腔覆盖层水下爆炸抗冲性能研究

李俊杰，陶 猛，叶韩峰

(贵州大学 机械工程学院,贵阳 550025)

舰船作为重要的海上战斗力已成为各国军事发展的主要组成，随着现代武器科技的发展，对舰船的抗冲击能力以及反探测隐身能力提出了更高的要求[1]。水下非接触性爆炸产生的冲击波作为最常见的破坏来源，目前国内外对敷设于舰船湿表面的防护层在水下爆炸冲击作用下的抗冲机理研究较多。Dharmasena等[2]分析了多种金属夹层板在水下平面冲击波作用下的动响应，并发现等效泡沫模型可以模拟在平面脉冲载荷作用下刚性支承夹层板的动态响应。Leblanc等[3]通过数值模拟和实验研究分析了复合芯层板的近场水下爆炸动态响应模式。Chen等[4]通过实验验证了在受爆炸冲击波时橡胶夹芯覆盖层对水下结构有较好防护作用，弱芯层在流固耦合作用下减小了入射冲量。由超弹性材料制成的声学覆盖层已被证明具有抗冲击和隔声双重性能[5-9]。水下爆炸实验开展难度高且测试误差大，目前对覆盖层抗冲性能的研究主要围绕抗冲机理展开，而芯层空腔类型和结构参数对覆盖层抗冲性能的影响研究较少。

具有负泊松比特性的蜂窝结构以其出众的力学性能和胞元微结构可设计性等优点已被广泛应用于缓冲、吸能材料[10]。对一种二维平面内具有负泊松比效应的多胞结构，卢子兴等[11]讨论了胞元内凹角度关系对其泊松比的影响。Zhang等[12]讨论了蜂窝细胞微拓扑性对面内冲击性能的影响，结果显示微结构影响了负泊松比蜂窝材料整体的动态响应和能量吸收能力。目前，对负泊松比蜂窝的研究主要集中在变形特性研究，在静态和准静态压缩下的力学性能研究等，而对其在冲击载荷作用下的动态分析较少，特别是其在水下爆炸冲击作用下的抗冲性能有待澄清。

本文以负泊松比橡胶蜂窝空腔覆盖层为研究对象，利用ABAQUS显示动力学软件对覆盖层在水下非接触性爆炸作用下的动态响应进行了分析。讨论了覆盖层高度、胞元壁厚和扩张角等参数对爆炸冲击波入射压力、能量耗散和被保护钢板动响应的影响，以期建立具有负泊松比效应的蜂窝空腔覆盖层结构参数与其水下抗冲性能的关系。

1 计算模型

1.1 负泊松比蜂窝胞元模型

图1给出了选取的负泊松比内凹六边形蜂窝胞元结构的力学分析模型，规定蜂窝结构的底边长度为h，两侧的倾斜边长l，蜂窝壁板倾斜边与竖直边的夹角为θ,壁厚为t。蜂窝覆盖层相对密度可表示为

(1)

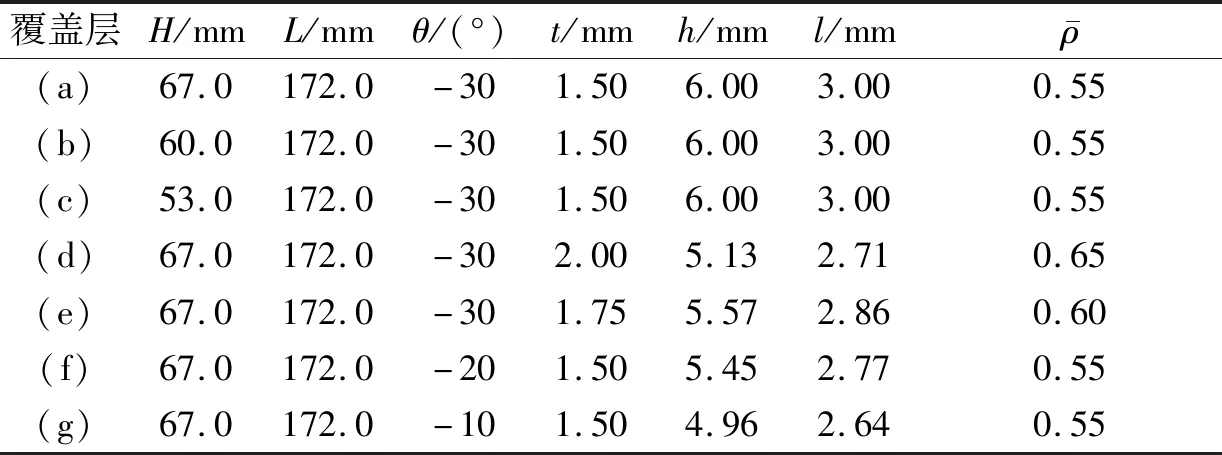
式中，ρ*为橡胶材料密度，ρs为基体材料密度，li、ti分别为第i个韧带长、宽，H、L分别为覆盖层高度和宽度。表1给出了各组覆盖层结构参数。

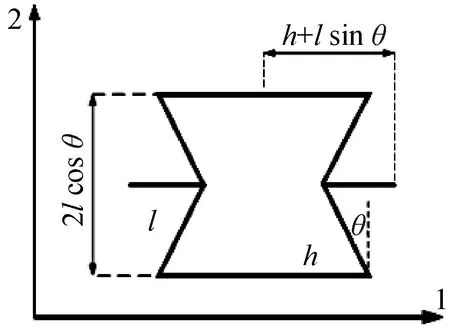
图1 负泊松比内凹六边形蜂窝结构胞元示意图Fig.1 Diagrammatic sketch for honeycombs with concave cells

表1 蜂窝覆盖层特征参数
Tab.1 Characteristic parameters for honeycomb claddings

覆盖层H/mmL/mmθ/(°)t/mmh/mml/mmρ(a)67.0172.0-301.506.003.000.55(b)60.0172.0-301.506.003.000.55(c)53.0172.0-301.506.003.000.55(d)67.0172.0-302.005.132.710.65(e)67.0172.0-301.755.572.860.60(f)67.0172.0-201.505.452.770.55(g)67.0172.0-101.504.962.640.55

1.2 流固耦合模型

根据水下爆炸模拟与实船试验数据对比[13]，ABAQUS声固耦合算法已被证明可较真实模拟水下爆炸载荷加载过程和结构响应的实际。在水下爆炸抗冲分析中，考虑包括流体和覆盖层结构的问题，当受到来自求解域外的入射波激励时，流固耦合方程为[14]

(2)

(3)

通常在流固耦合面上，结构与声学流体介质在耦合面法线方向完全耦合，具有相同的位移边界，但在切向运动上是不耦合的。而Sfrs表示在流固耦合面上具有声学介质(阻抗边界)的特殊情况，此时，结构与流体线形耦合但并不一定完全相等。而在流体方程中，Sfr为阻抗边界；此边界上，流体声压与其法向导数呈线性关系。Sfi为非反射边界，用有限的流体域模拟无限场。

图2给出了包括负泊松比蜂窝覆盖层和对应流体域的水下非接触性爆炸流固耦合有限元计算二维平面模型。进行覆盖层水下爆炸模拟分析时,需建立足够大的外部流场以减少流场的重力、阻尼及惯性影响，当外部流场高度为覆盖层的6倍时，附连水质量率接近1，这里为获得较为准确的响应取矩形流场高度为420 mm。忽略应力波在流体域边界处的反射及应力回弹，对流体域边界设置无反射边界条件以模拟无限大水域。覆盖层和钢板均采用四节点四边形双线性减缩积分单元(CPE4R)划分，覆盖层、钢板网格单元分别为0.6 mm、1 mm，矩形水域采用四节点四边形线性声学单元(AC2D4R)划分，网格单元0.5 mm。水域与覆盖层接触面设置耦合边界条件以传递应力和位移。覆盖层左右两侧表面设置对称边界条件以近似模拟无限大范围，将覆盖层空腔内壁设置为自接触属性以防止计算过程中覆盖层大变形引起材料间的穿透。模型底端为被防护的钢板，钢板高4 mm,长1 000 mm，考虑覆盖层敷设在船体湿表面，为更好地反映弹性支撑下覆盖层抗冲性能，将钢板两侧固支。

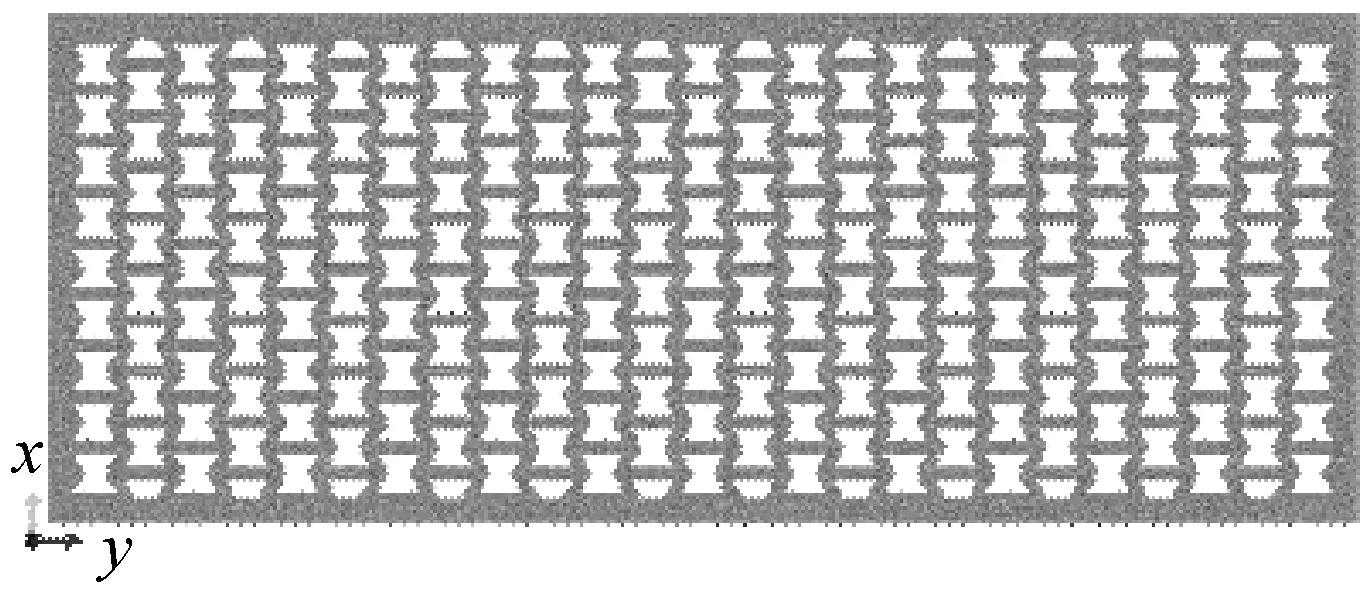
(a)负泊松比蜂窝覆盖层有限元模型

(b)水下爆炸二维计算模型图2 有限元计算模型Fig.2 Finite element calculation model

因爆炸作用的瞬时性及面板材料的大变形等特点，借助ABAQUS/Explicit对其进行非线性分析。由于橡胶材料覆盖层受冲击后上表面快速变形特性，采用考虑空化效应的总波公式。在近场水域中未考虑流体自重因而设置发生空穴现象临界压力为0 MPa。计算模型中爆炸冲击波为球面波，水域顶端中点设置为爆源，流固耦合面中点为爆炸接触点，计算过程中冲击波将自动加载于覆盖层上表面。水下爆炸冲击波的计算沿用库尔公式[15]

(4)

式中：t为时间，单位ms；P(t)为随时间变化的冲击波载荷，单位MPa；M为TNT炸药质量，单位kg；R为爆炸距离，单位m；q为爆炸冲击衰减时间因子；Pm为爆炸初始峰值，单位MPa。这里取15 MPa压力幅值冲击波，图3给出了冲击波载荷在1 ms内指数衰减曲线。

图3 冲击波载荷示意图Fig.3 The curve of shock pressure

1.3 覆盖层橡胶材料本构模型

覆盖层材料采用文献[4]中的邵氏硬度65氯丁橡胶。一般认为橡胶为不可压缩的各向同性材料，其高度的材料非线性特性可用超弹性模型描述。图4给出了覆盖层所用材料试件的单轴拉压实验数据与最常用的Mooney-Rivlin和适用于大应变的Arruda-Boyce超弹性本构模型拟合曲线。可以看出，常用的唯象一次模型Mooney-Rivlin的应变能是不变量的线性函数，在超过100 %的大应变区域不能反映准确的应力应变关系。Arruda-Boyce八链模型对试件在大应变区的模拟更为合理。在计算中覆盖层橡胶材料采用Arruda-Boyce本构模型μ=0.996 890 263，λm=2.960 611 46，D=0，单位均为MPa，且材料密度为1 500 kg/m3。

图4 橡胶材料应力-应变曲线图Fig.4 Stress-strain curve of rubber material

2 覆盖层动态响应分析

2.1 浅水爆炸下的覆盖层动态响应

对于所研究问题属于浅水非接触性爆炸响应，通常不考虑静水压力作用。负泊松比蜂窝覆盖层局部变形机制是影响其对于入射能量的吸收及承载能力的重要因素。图5给出了覆盖层在受水下爆炸冲击过程中的瞬态响应。冲击波到达覆盖层上表面后一部分透射进入覆盖层，一部分发生反射。覆盖层上表面接收到爆炸冲击波后部分能量透射进入覆盖层内部，表面产生较大变形，上层空腔被压缩屈曲(图5(a))。急速衰减的入射波与瞬时产生的较大反射波叠加，产生负压现象。当局部区域负压值超过该处流体域空化压力极限，便在该处出现局部空化现象，以至于上层空腔并未被压溃。随着空化区域的上升，被空化拉断的水介质回弹到附加水层上，为覆盖层表面提供能量，再次呈现正向残余应力加载。

应力波沿着最短路径向下传播，在覆盖层内部的应力沿着内凹六边形胞元韧带由纵波转换为弯曲波和横波，再重新转换为纵波，往复进行。这一过程同时伴随着胞元的屈曲压垮直至覆盖层整体的大变形(图5(c))。可以看出，覆盖层内应力集中点位于胞元转角处，复杂的波形转换过程耗散掉大量能量。应力波到达覆盖层底端后大部分应力波透射进入钢板，钢板随即获得加速度响应。橡胶波阻抗远小于钢，大量应力波通过覆盖层底端面透射进入钢板，之后覆盖层的惯性效应在变形特性中更加显著。

(a)t=0.1 ms

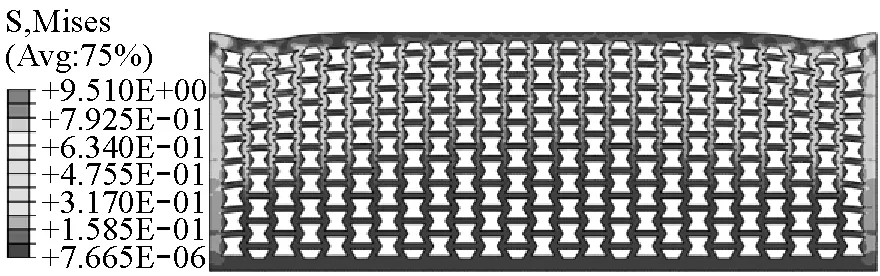
(b)t=1.0 ms

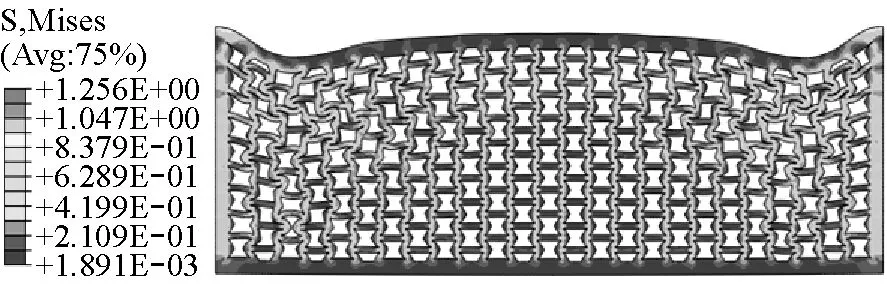
(c)t=3.0 ms

(d)t=6.0 ms图5 冲击波作用下覆盖层瞬态响应Fig.5 The response of the cladding under shock wave

2.2 静水压力对覆盖层动态响应的影响

抗冲覆盖层处于水下环境，不可避免地受到静水压力的作用，从而导致空腔覆盖层抗冲性能受到影响。这里分析在静水压力条件下负泊松比空腔覆盖层受水下爆炸作用的动态响应，以揭示覆盖层在不同环境下的抗冲特性。在ABAQUS声固耦合计算中，静水压力仅为空化效应的产生提供依据，而不影响水中动压和流固耦合的计算。这里以水域爆炸源点和覆盖层上表面爆炸接触点为参考点，设置两参考点的静水压力，程序线性计算水域所有节点的静压。图6给出了与2.1相同爆炸冲击作用下覆盖层在105Pa静水压力条件下的动态响应。可以看出，静压下覆盖层在响应初期(0.1 ms内)上层空腔已被瞬时入射的峰值压力压溃至局部密实化(图6(a))。静水压力的存在使得覆盖层上表面周围水域压力更难达到负压值，进而更难形成局部空化区域。之后上层空腔恢复变形(图6(b))，且空腔处于上下拉伸变形状态。随着应力波的向下传递，覆盖层呈现出逐层被压实后再恢复变形。在应力波到达底端后，部分反射波与残余加载应力波叠加，覆盖层空腔开始无序的屈曲变形。可以看出，静水压力明显减弱了覆盖层外部水域形成局部空化的能力，这将导致更多的能量入射覆盖层。而在响应后期，应力波在覆盖层内的传递和覆盖层整体变形机制受静水压力的影响不大。

(a)t=0.1 ms

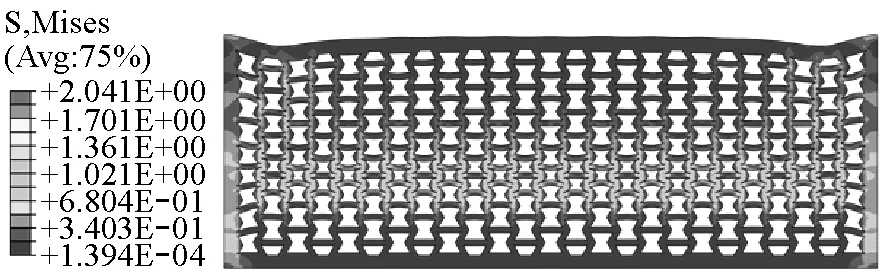
(b)t=1.0 ms

(c)t=3.0 ms

(d)t=6.0 ms图6 静压条件下覆盖层瞬态响应Fig.6 The response of the cladding under hydrostatic pressure

2.3 有无覆盖层对钢板响应的比较

表2给出了不考虑静水压力影响和在105Pa静水压力两种工况下的裸钢板和敷设覆盖层钢板响应峰值。敷设覆盖层钢板的吸能和上表面中点位移明显减小，覆盖层能有效缓冲吸能。另外，静压对裸钢板的响应影响很小，静压环境下吸能增加14.6%，最大位移增加0.7%。而对于敷设覆盖层钢板，静压下吸能增加30.0%，最大位移增加14.4%。可以看出，静水压力的存在对易于大变形形成空化的覆盖层抗冲性能有一定影响。

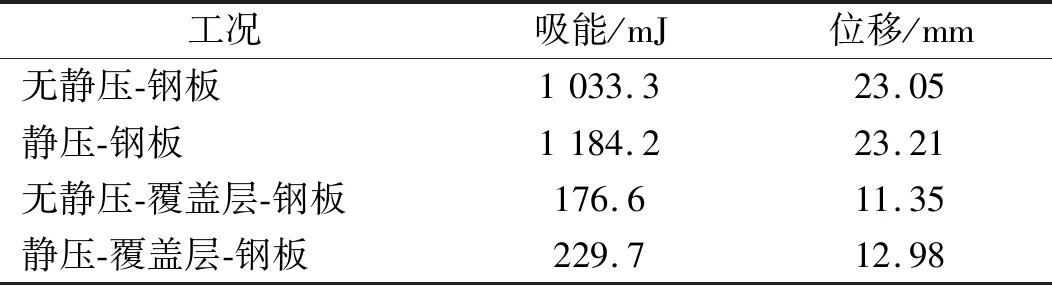
表2 钢板响应峰值Tab.2 The response peaks of plate

3 覆盖层结构参数对抗冲性能的影响

本节分别讨论覆盖层高度、胞元壁厚和扩张角度等结构参数对覆盖层抗冲击性能的影响。给出水下冲击波载荷作用下(这里不考虑静水压力作用)，各组覆盖层对入射波的流固耦合作用，应力传递规律和能量耗散。最后，以底端钢板上表面中点作为参考点，通过参考点加速度响应和最大位移直观反映覆盖层的抗冲缓冲能力。表3给出了各覆盖层的计算详细结果。

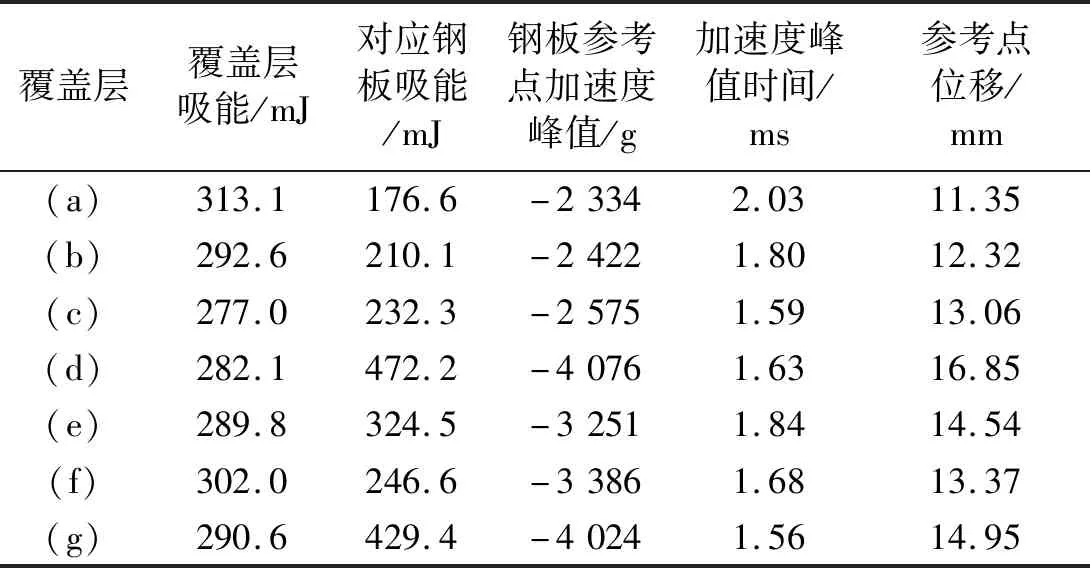
表3 各组覆盖层计算结果Tab.3 The calculation results of claddings

3.1 高度对抗冲性能的影响

在胞元扩张角(θ=-30°)和壁厚(t=1.5 mm)不变的条件下，通过改变空腔层数得到高度分别为67 mm、60 mm、53 mm三组覆盖层。图7给出了不同高度覆盖层在压力幅值为15 MPa的冲击波作用下的时历响应。

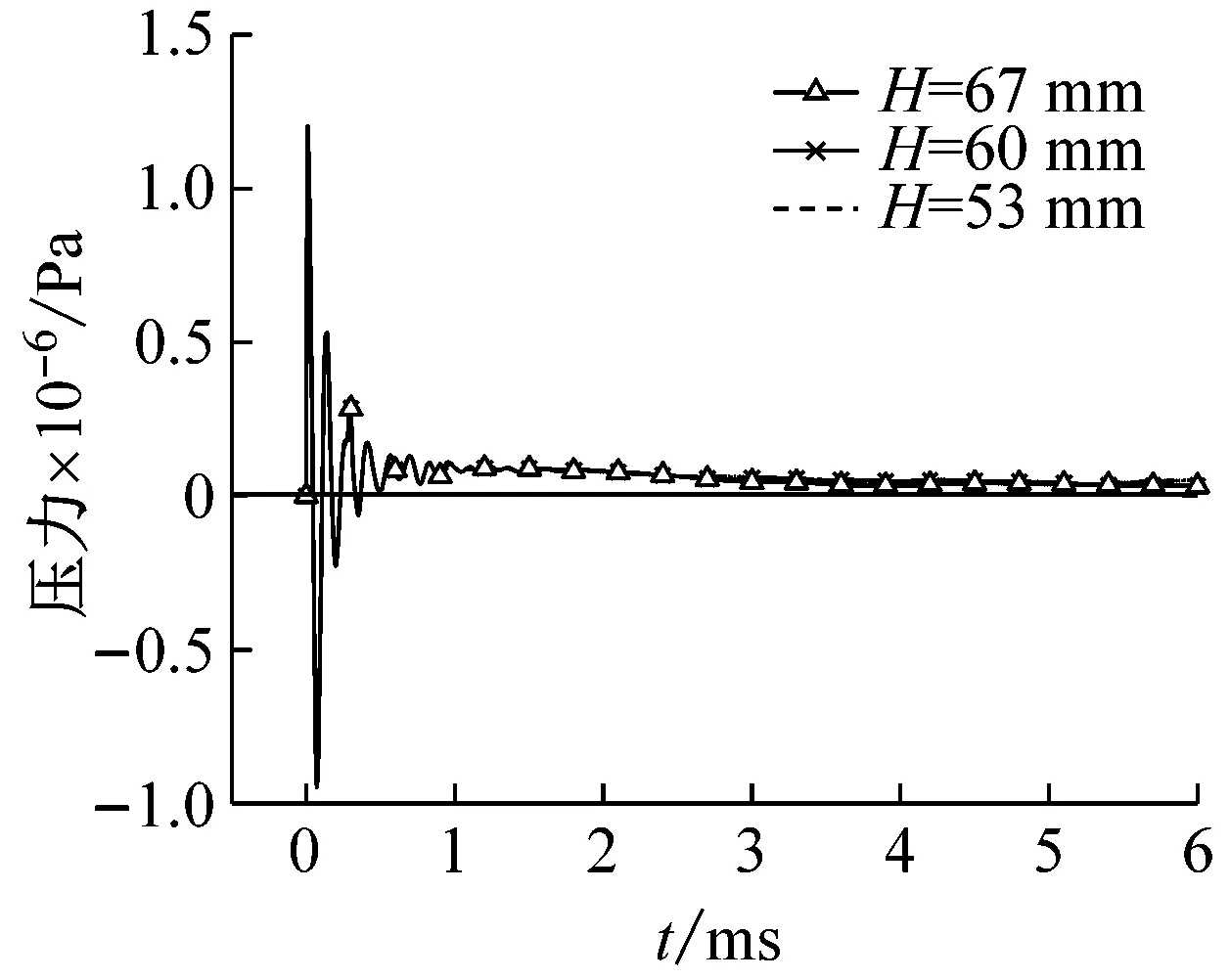
图7(a)为覆盖层流固耦合面压力时历曲线。初始时刻出现压力峰值随后大幅度衰减，与爆炸冲击波特点一致。入射覆盖层的冲击波部分反射回流体域，同时负泊松比结构的覆盖层受到峰值压力随即产生大变形，在耦合面处急速衰减的入射波与瞬时产生的较大反射波叠加，形成局部空化区域出现负压。随着空化区域的上升，被空化拉断的水介质回弹到附加水层上，为覆盖层表面提供能量，再次呈现正向压力加载。在响应初期，出现往复的高频震荡。由于能量在覆盖层中传递和相互作用过程中的快速衰减，耦合面上压力逐渐呈现平稳，且接近零线。可以看出，覆盖层芯层空腔分布形式相同、胞元参数相同的条件下，高度的改变对入射压力影响很小。在响应前期的高频震荡时段应力波处于向下传递阶段，不同高度覆盖层上表面流固耦合作用和应力传递规律一致。响应后期残余应力的加载过程中，幅值差距依然很小。

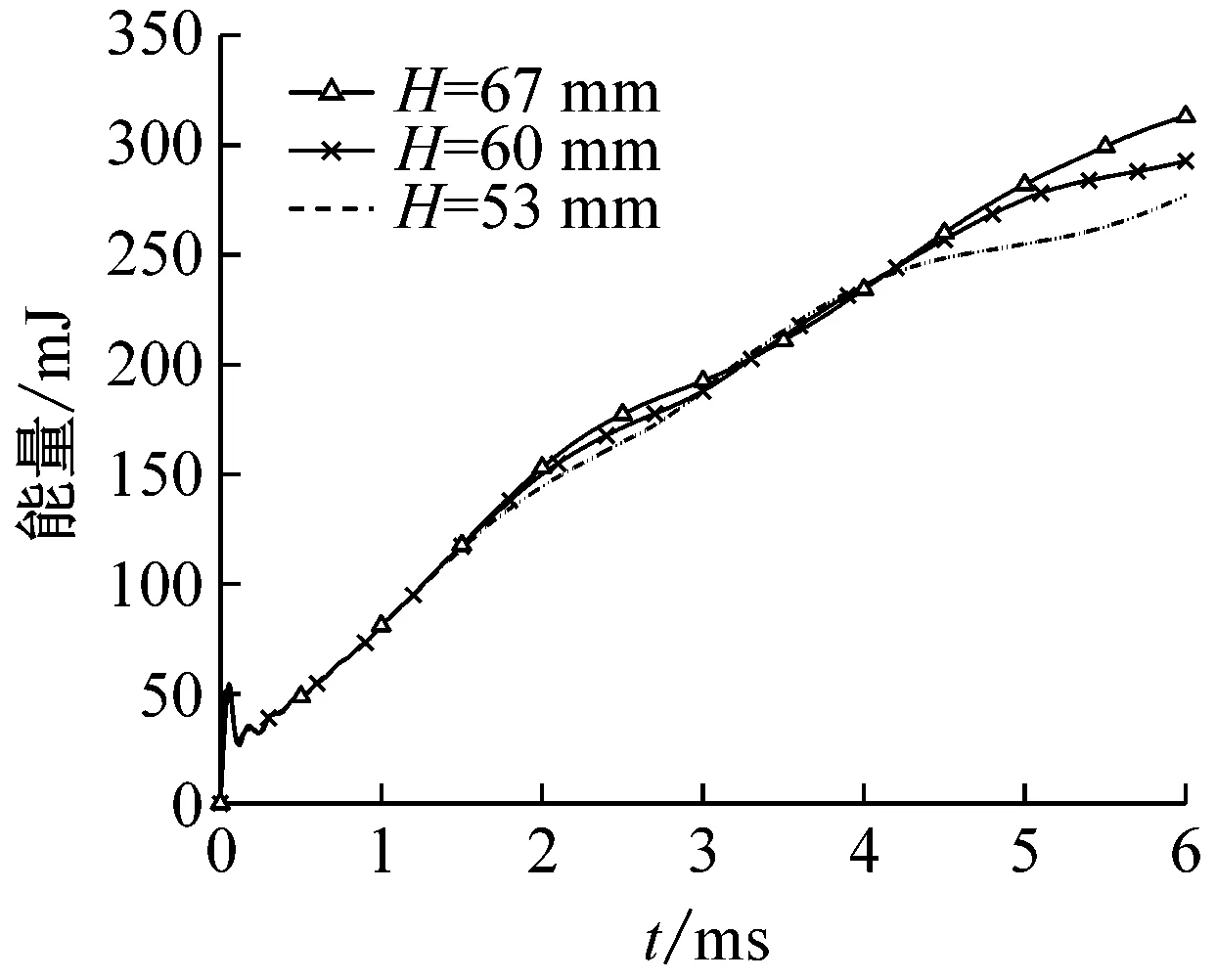
在爆炸冲击波作用下，覆盖层产生的动能和自身变形吸能为主要能量耗散形式，这里将动能与内能的总和作为覆盖层的吸收能量。图7(b)为覆盖层吸收能量时历曲线。在冲击波入射瞬间，覆盖层通过流固耦合作用获得入射冲量随即吸收能量在初始时刻出现阶跃上升。在应力波传播过程中波速远大于材料变形速度，覆盖层整体动能有所下降。在应力波向下传递过程中，覆盖层处于弹性压缩阶段，内能不断升高。在相同胞元结构和分布形式的覆盖层中，高度的改变没有影响应力波传递规律。响应后期，随着高度的增加，惯性效应显著，变形储能吸收更多能量。

图7(c)为底端钢板参考点加速度时历曲线。爆炸冲击波经覆盖层传递到钢板，钢板随即得到向下的加速度。从参考点加速度响应时历来看，不同高度覆盖层响应趋势相同。在应力波到达钢板后随即得到向下的最大加速度。应力波的触底反射让参考点获得向上的加速度，但在数值上较向下加速度小。响应后期，通过复杂路径传递的应力波得到大幅衰减，覆盖层整体的惯性效应明显，使钢板再次得到向下的加速度，但震荡幅值较响应前期小。高度分别为53 mm、60 mm、67 mm三组覆盖层低端钢板参考点分别在1.59 ms、1.80 ms、2.03 ms迎来加速度响应峰值，峰值大小分别为2 575.4g、2 421.6g、2 334.3g。随着高度的增加，应力波在覆盖层内传递路径更远，到达底端时间更长，抗冲和缓冲效果更优，最终底端钢板吸能减少，最大位移减小。结果与文献[9]中对手性蜂窝覆盖层高度对水下抗冲性能影响的研究结果一致。

(a)压力

(b)能量

(c)加速度图7 不同高度覆盖层的响应曲线Fig.7 Response curves of the claddings with different height

3.2 胞元壁厚对抗冲性能的影响

图8给出了同一高度(H=67mm)和胞元扩张角(θ=-30°)壁厚t分别为1.50 mm、1.75 mm、2 mm的三组覆盖层在15 MPa压力幅值冲击波水下爆炸作用下的响应曲线。

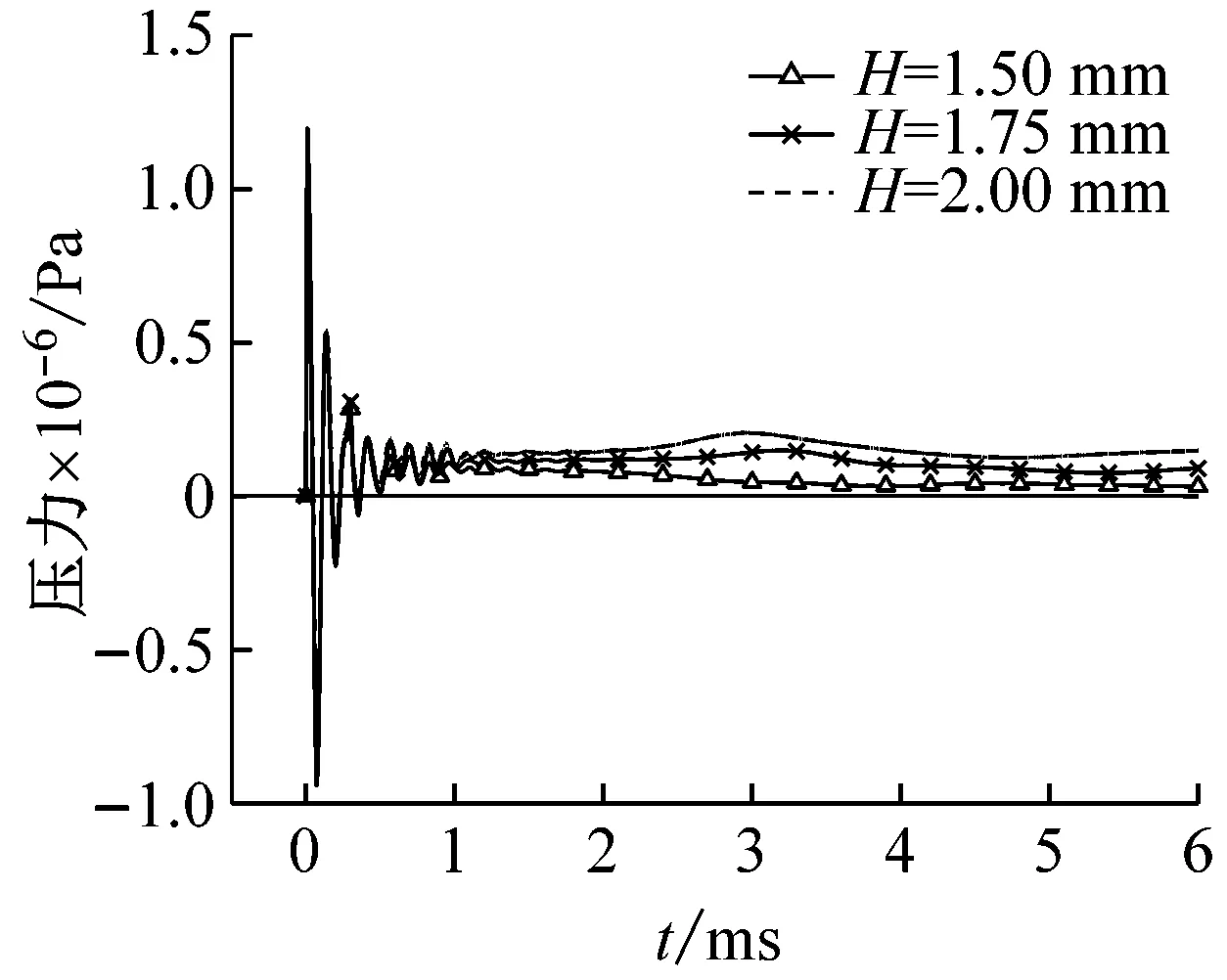
图8(a)为覆盖层流固耦合面压力时历曲线。可以看出，胞元壁厚影响耦合面上压力的大小，随着壁厚的减小，覆盖层整体更易变形，类似空气弹簧作用的空化区域更易形成，耦合面上残余应力加载减少。

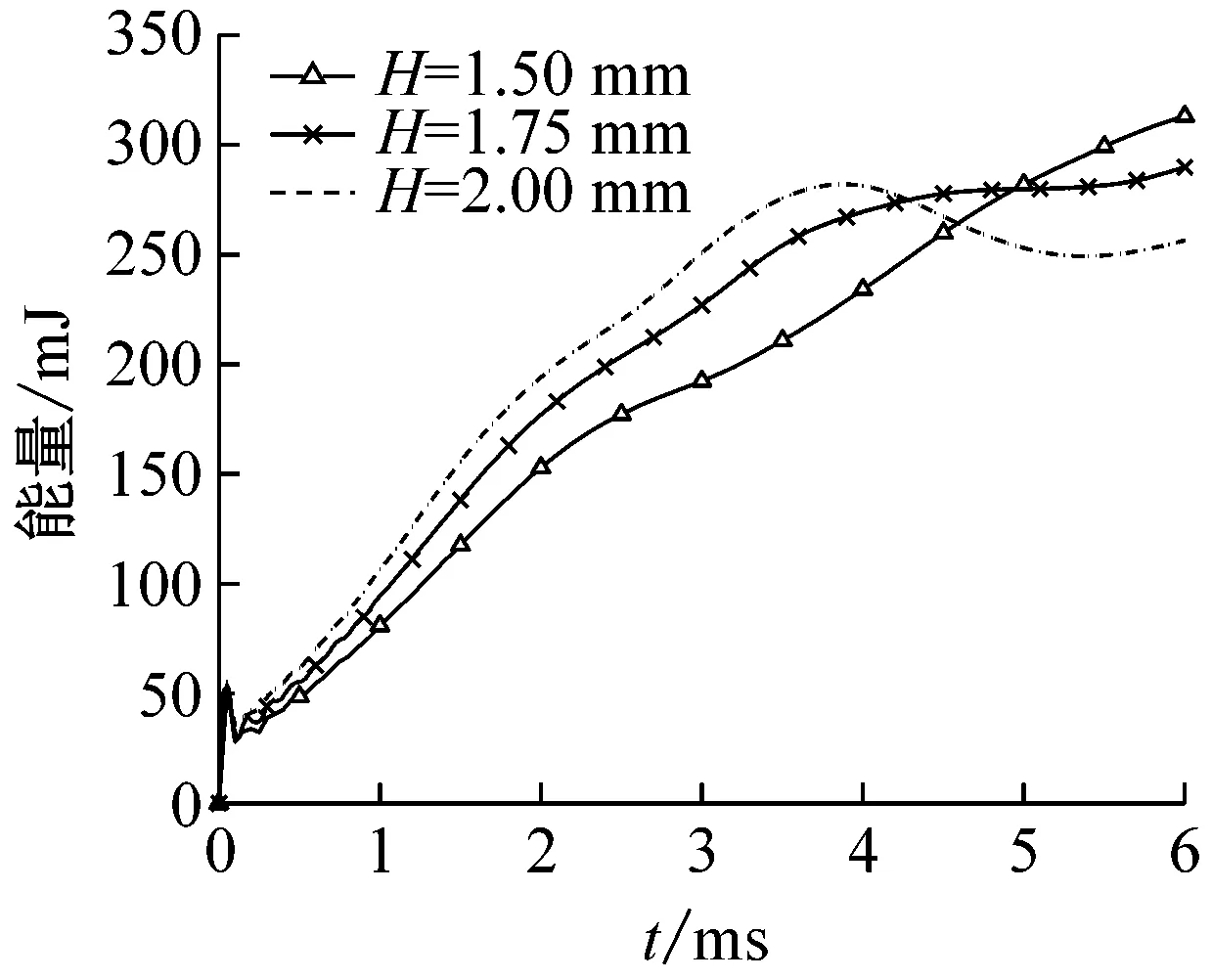
图8(b)为覆盖层吸收能量时历曲线。通过数值比较可以看出，响应前期，在覆盖层没有出现胞元压溃和整体变形现象之前壁厚越大的覆盖层呈现出更大的整体刚度，获得更多的能量。在约4 ms之后，覆盖层大量胞元屈曲变形或者垮塌。随着壁厚减小，覆盖层更易发生大变形，整体压缩量更大，吸收更多的能量。

图8(c)为钢板参考点加速度时历曲线。壁厚分别为2.00 mm、1.75 mm、1.50 mm的三组覆盖层对应钢板参考点加速度响应峰值分别为-4 076g、-3 251g、-2 334.3g，响应峰值对应时间分别为1.63 ms、1.84 ms、2.03 ms。随壁厚减小，参考点加速度峰值减小且峰值时间更晚。壁厚越小覆盖层相对密度越小，变形程度越大，应力波在覆盖层中的波形转换越复杂，同时耗散更多能量，钢板得到的传递应力和吸能得到大幅衰减，参考点最大位移减小。壁厚的减小提高了覆盖层抗冲能力，但在水下应用背景下还需考虑覆盖层的整体刚度以保证其在一定水深下的抗变形能力。

(a)压力

(b)能量

(c)加速度图8 不同壁厚覆盖层的响应曲线Fig.8 Response curves of the claddings with different wall thickness

3.3 胞元扩张角对抗冲性能的影响

图9给出了同一高度(H=67 mm)和壁厚(t=1.50 mm)胞元扩张角θ分别为-30°、-20°、-10°的三组覆盖层在15 MPa压力幅值冲击波水下爆炸作用下的响应曲线。

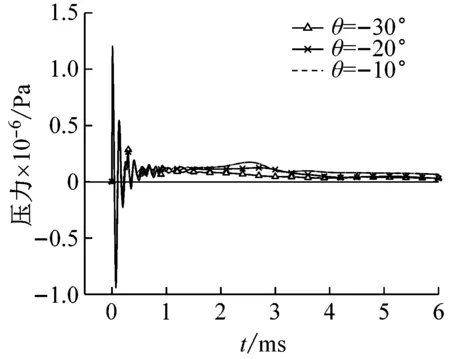
图9(a)为覆盖层流固耦合面压力时历曲线。胞元扩张角的变化并没有影响覆盖层流固耦合面冲击波入射特性，各组覆盖层耦合面上压力时历特点相似。胞元扩张角绝对值的增大使覆盖层的负泊松比效应增强，在冲击波入射瞬间产生的整体变形效应显著，应力波在较大胞元扩张角的覆盖层中传递路径更长，在转角处的波形转换耗散更多能量，耦合面上压力更快趋近于零线。

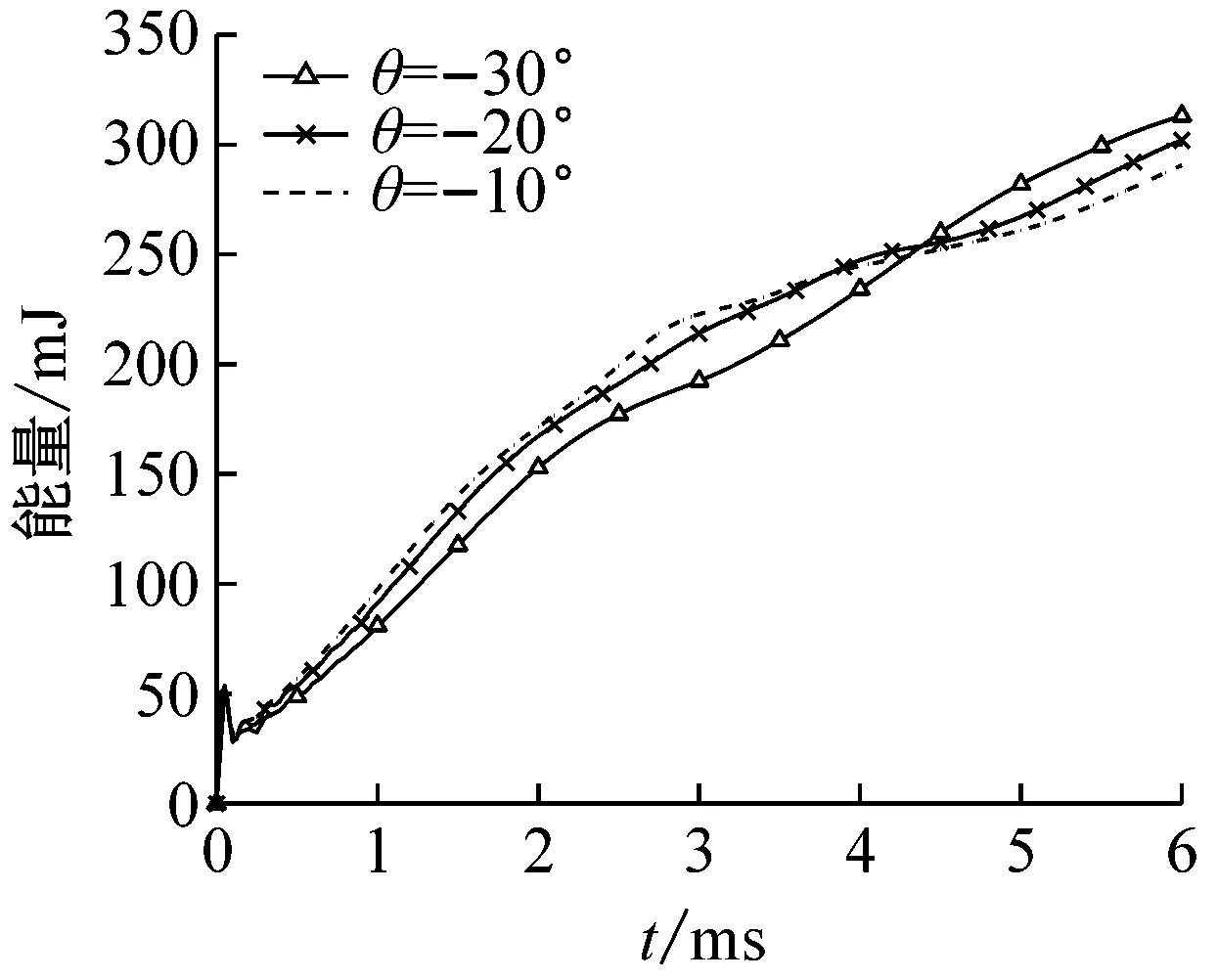
图9(b)为覆盖层吸收能量时历曲线。可以看出，胞元扩张角的改变影响了覆盖层能量吸收特性。在覆盖层没出现整体垮塌(4.5 ms之前)阶段，随着扩张角绝对值的增加，覆盖层面内更加稳定胞元韧带不易变形，吸收能量减小。而在覆盖层开始出现整体垮塌后，随着扩张角绝对值的增加，由于应力集中在节点处，胞元被压溃后更易调动周围胞元发生整体变形，吸收更多的能量。

图9(c)为钢板参考点加速度时历曲线。随着胞元扩张角绝对值的增大，覆盖层呈现出更好的稳定性。θ=-20°和θ=-10°的覆盖层对应钢板参考点在4 ms时间附近较θ=-30°的加速度幅值震荡剧烈，特别是θ=-10°覆盖层参考点尤为明显。

从加速度幅值大小来看，胞元扩张角越大，参考点向下的加速度越小且峰值时间推迟。胞元扩张角θ分别为-10°、-20°、-30°的三组覆盖层对应钢板参考点加速度响应峰值分别为4 020.2g、3 386.0g、2 334.3g，响应峰值对应时间分别为1.55 ms、1.67 ms、2.03 ms。随扩张角绝对值的增大，应力波在向下传递过程中路径变长，纵波横波之间的波形转换更多，应力波到达覆盖层底端的时间变长。同样的，在更为复杂的传递路径和波形变换过程中，伴随着更多的能量耗散，特别是纵波转换为横波的过程更为显著，最终底端钢板吸能减少，最大位移减小。在θ=-30°覆盖层中应力波传递路径中较多的纵波转换为横波，参考点加速度响应峰值减小和峰值出现时间迟缓较其他两组覆盖层尤为明显。

(a)压力

(b)能量

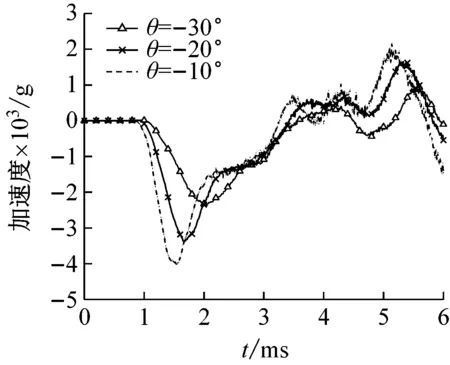
(c)加速度图9 不同扩张角覆盖层的响应曲线Fig.9 Response curves of the claddings with different expanding angle

4 结 论

针对具有负泊松比特性的蜂窝空腔覆盖层建立了水下爆炸抗冲模型。结果表明，负泊松比蜂窝空腔覆盖层通过流固耦合作用减小了入射压力，应力波向下传递过程中的波形转换和覆盖层吸能耗散掉大量能量，使其具有优良抗冲性能。需要指出的是，静水压力的存在导致临近水域局部空化更难形成，这对蜂窝空腔覆盖层抗冲性能有一定影响。

在同一峰值压力冲击波作用下，覆盖层高度、胞元壁厚和扩张角的改变影响了覆盖层抗冲性能。具体表现为：

(1)在保证覆盖层承压和不发生严重密实化条件下，随着覆盖层高度增加，更长的应力传递路径减小了低端钢板加速度响应峰值，推迟峰值时间。

(2)胞元壁厚减小，覆盖层相对密度减小，更大的空化区域使得流固耦合接收到的压力减小，之后覆盖层整体大变形耗散掉更多能量，底端钢板参考点加速度响应减弱。

(3)胞元扩张角绝对值增大，覆盖层负泊松比特性显著，响应前期的空化效应减弱入射压力，传递应力集中在节点处调动整体大变形吸收更多能量，底端钢板参考点加速度响应峰值减小，峰值时间推迟，覆盖层表现出更好的抗冲和缓冲特性。