基于强震响应过程信息的大坝损伤识别研究

李 静,陈健云,徐 强,顾太欧

(大连理工大学 建设工程学部，大连 116023)

我国西部强震区兴建了大量的库容巨大水利工程，其设计地震烈度多在VIII～IX 度之间，如大岗山拱坝达到0.56g，一旦发生破坏会造成无法估量的后果。良好的设计是保障混凝土大坝抗震安全最关键因素，但是，由于各种不确定性或随机性因素的影响，大坝在运行过程中总会出现各种难以预料的风险，包括地震动的作用，如印度的Koyna大坝按峰值加速度0.05g的地震动设计，但在1967年遭受的地震动，水平向达0.49g，竖直向达0.34g。因此，水工大坝普遍采用监测系统对运行状态进行实时监测。

基于大坝监测信息的安全诊断目前的研究很多，但主要集中在正常运行阶段的监测信息异常及原因分析。基于大坝动态响应的模态识别研究相对较多[1]，遭受强震作用后的损伤识别及判断方面的研究相对较少。

当前结构的损伤识别包括：损伤是否发生、损伤位置、损伤程度、结构可维持的寿命。对这几个问题国内外已经已经发展了多种方法。Cawley等[2]利用固有频率对结构进行只存在单处损伤的情况下的损伤识别。Juneja等[3]提出了对比最大化的方法，将结构损伤前后的结构响应阵进行对比分析，判断结构是否损伤。Pandey等[4]由梁损伤前后结构模态曲率变化研究梁的损伤位置与程度；Pandey等[5]利用柔度矩阵对结构是否损伤与结构损伤位置进行了研究；Wu等[6]将BP神经网络用于一刚性楼板三层框架土木建筑工程结构的损伤识别研究；

对于大型复杂结构采用基于损伤前后的动态信息进行损伤识别有一定的难度。这是因为对于大型结构，结构损伤之前的动力参数不易获得；而且对整个结构进行完整详细的动态监测显然有些不切实际。损伤作为高频模态表征的局部现象，在损伤较小时，对于结构整体动态特征的影响不明显，隐藏在局部信号里的损伤在模态信息中很难发现。目前的数学变换方法以及采样频率对高频分析还存在不足之处。

近年来，小波分析在混凝土结构的损伤识别和健康监测领域中也取得了一定的进展[7]。李洪泉等[8]对钢筋混凝土框架地震台试验获得的位移时程信号进行小波变换，根据分解后的信号在大尺度下是否有明显的幅值变化判断是否发生损伤；Hou等[9]通过数值模拟和实际结构的振动试验获取时域信号，对时域信号进行小波变换识别损伤时刻；Hera等[10]通过多种模型分析发现在损伤发生时刻小波分解图出现奇异点；陈隽等[11]采用小波分析三层剪切型结构振动台试验测得的结构加速度信号来识别结构损伤发生的时刻和位置；刘红坡等[12]分析了加速度、速度和位移时程信号，对其进行小波变换进行损伤识别，结果表明此种方法能识别损伤发生的时刻。余竹等[13]利用小波分析的Lipschitz指数对连续梁的损伤进行了定位及程度识别；

实际上，仅在震后识别坝体损伤程度和损伤位置，对于判断大坝震后安全或采取应急措施是不够的，还应该了解强震过程中大坝的损伤发展路径，不仅可以更为合理的判断大坝可能失效模式和风险，而且对于提高抗震设计水平和抗震措施也是有重要价值。

本文针对以上问题，结合小波分析方法和相关性分析方法，提出利用大坝强震过程中的加速度响应时程信息，识别不同位置的损伤、出现时刻以及损伤程度，实现大坝的在线实时损伤预警，为今后利用强震监测信息识别大坝强震失效模式提供参考。

1 小波分析基本理论

大坝损伤发展路径和破坏模式的识别，不仅要识别出损伤位置，还要识别出不同部位损伤发生的时刻，从而构成损伤的时间序列和空间路径。传统的傅里叶变换其频率分辨率高，但在时域上无定位能力。小波变换的基函数具有离散正交性，其在时间域与频率域上的伸缩与平移对强震过程中由于损伤发生而引起的信号非平稳变化的识别具有优势。

设φ(t)为一个基本小波(Mother Wavelet)，经过伸缩与平移后得到一个小波系列

(1)

式中,b为平移因子，a为尺度因子。在不同尺度下，小波变换的时间信息由尺度因子a控制，小波的持续时间随着尺度因子a的增大而增宽，减小而缩短。

小波变换的本质是将基本小波函数φ(t)利用平移因子b的变化观测整个信号的时间轴，然后在不同尺度因子a下展开

Wx(a,b)=〈x,φa,b〉=

(2)

由式(2)可以看出，小波变换的实质是把分析信号x(t)看作是由若干个小波系数Wx(a,b)组成的，而这些小波系数可以对原函数进行重构

(3)

当尺度因子a增加或者减小时，表示以延伸的或者缩短的φ(t)波形去观察x(t)的整体或局部，当a增大时，频率分辨率高，当a减小时，时间分辨率高。

结构响应过程中频谱特征发生变化通常有两种可能性，一个是地震动激励的频谱特征发生变化，一个是大坝的动态特性发生变化。大坝在强震中的损伤会引起坝体动态特性发生变化，对结构动态特性的扰动随着损伤的发展从局部高阶模态逐渐向低阶模态扩散，在结构响应中会包含这种变化。

当信号中存在突变点时，那么在突变点附近的各个尺度上的小波变换系数都会产生一个局部极大值，并且随着尺度的减小，这些模的局部极大值点逐渐收敛于突变点。可以采用小波变换小尺度上的系数做为判断信号奇异性的标准。利用小波分解可以检测出信号上突变点的位置、类型以及变化的幅度，也就识别出损伤逐渐发展的时间过程。

2 基于强震响应时程信息的损伤识别预警指标

2.1 振动台模型试验

水工大体积混凝土结构主要利用混凝土的受压承载能力，抗压安全裕度很大，在强震作用中的破坏主要是受拉损伤开裂。本文针对某重力坝进行了振动台缩尺模型试验，模型高203 cm，采用满足高密度、低模量、低强度的重力相似准则的仿真混凝土材料浇注。弹性模量取51 MPa，密度取3 020 kg/m3，泊松比为0.167，阻尼比为0.05，实验模型如图1所示。输入规范谱水平向和竖直向地震波，竖向峰值加速度为水平向的2/3。通过人工波逐级加载，利用加速度传感器获得结构不同高程处的加速度响应信号。传感器布置如图2所示。

图1 实验浇筑模型Fig.1 Theexperimentalmodel图2 传感器布置Fig.2 Sensorlocation

图3为0.15g和0.55g地震波加载下及震后白噪声激励作用下模型动力响应时程的频谱分析结果。从图3可见，0.15g地震动作用下，基于大坝地震动响应过程的频谱分析得到的大坝基频略低于基于震后白噪声激励的响应时程频谱分析得到的结果，不过基本相差不多。这是因为0.15g作用下大坝损伤很小，震中和震后的材料性能相差不多。但是，0.55g地震动作用下，基于强震作用过程中的响应信号得到的大坝基频明显低于震后白噪声激励下得到的频率。这是因为0.55g地震动作用下结构损伤很大，在强震过程中体现出明显的非线性变化，试验中可以观察到大坝下游折坡处出现明显的裂缝并迅速向下游扩展，裂缝大约12 cm。而强震后坝体只承受自重和静水压力等作用，部分在强震过程中因受拉损伤开裂的部位在静力作用下处于受压闭合状态，比如下游折坡处的裂缝，震后的白噪声激励不足以使实际受到的损伤开裂特征重新显现出来。

(a)0.15g地震动作用

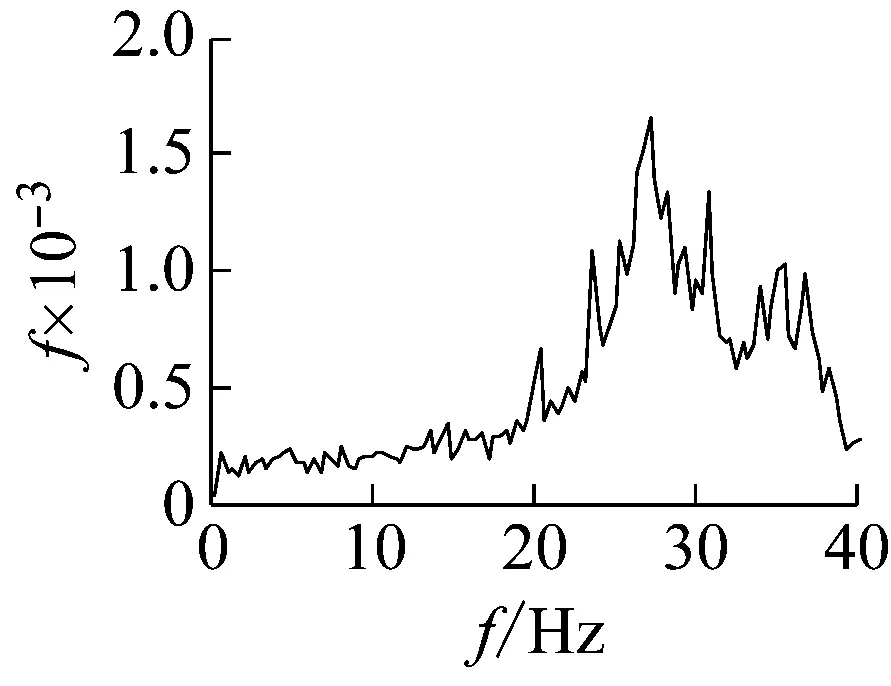
(b)0.15g震后白噪声激励

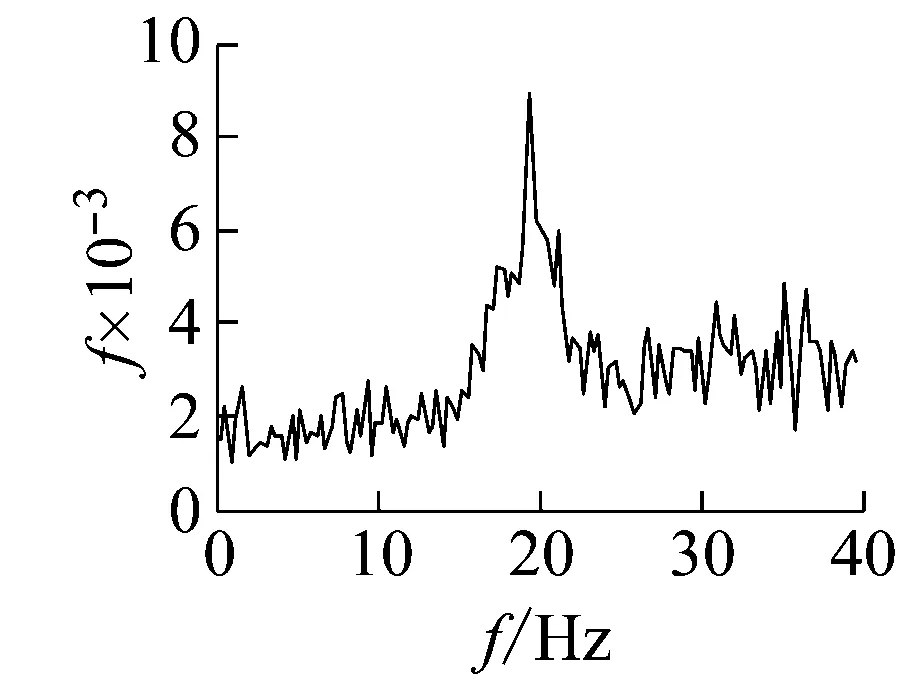
(c)0.55g地震动作用

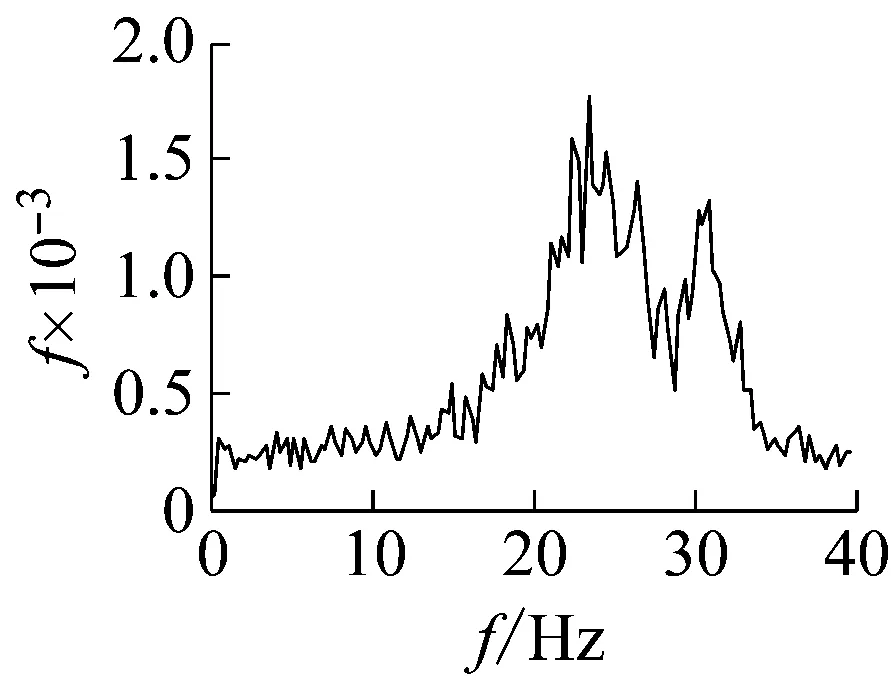
(d)0.55g震后白噪声激励图3 地震动作用下重力坝结构响应频谱Fig.3 Seismic response spectrum of gravity dam

结构损伤是在强震过程中产生的，反映到结构响应信号中则是损伤时刻的突变。基于震后脉动响应信号的分析，并不能重现实际损伤对应的应力状态，而且脉动响应信号信噪比低，因此，采用强震作用前后基于环境脉动的结构动力特性对比，并不能反映出大坝的真实损伤破坏状态，这对于大坝制定合理的震后修复加固措施是不利的。

直接利用强震过程中的非线性响应时程信息，可以避免了强震前后的信息对比，而且信噪比高，实时性和可信性更高，特别是可以通过不同部位的信号突变时刻的识别，获取损伤发展过程信息。因此，需要采用基于大坝强震响应过程中实时信号对坝体损伤破坏状态进行评估。本文选择具有4阶消失矩的db4小波进行分解，分解次数为3，结果如图4所示。

从图4中的分解信号d1、d2、d3可见，只在分解信号d3上能明显看到突变峰值，这是由于在该频带上由输入地震动荷载引起的加速度能量分布较小，而由坝体损伤引起的加速度变化能量分布较大，坝体损伤信息在该频带上被很好的表现出来了。但是，即使是d3，与开裂相对应的突变前也有大量的波动幅值，一方面是初始损伤到宏观裂缝形成之间的损伤不断发展造成的，另一方面也可能是监测信号中的大量噪声引起的。

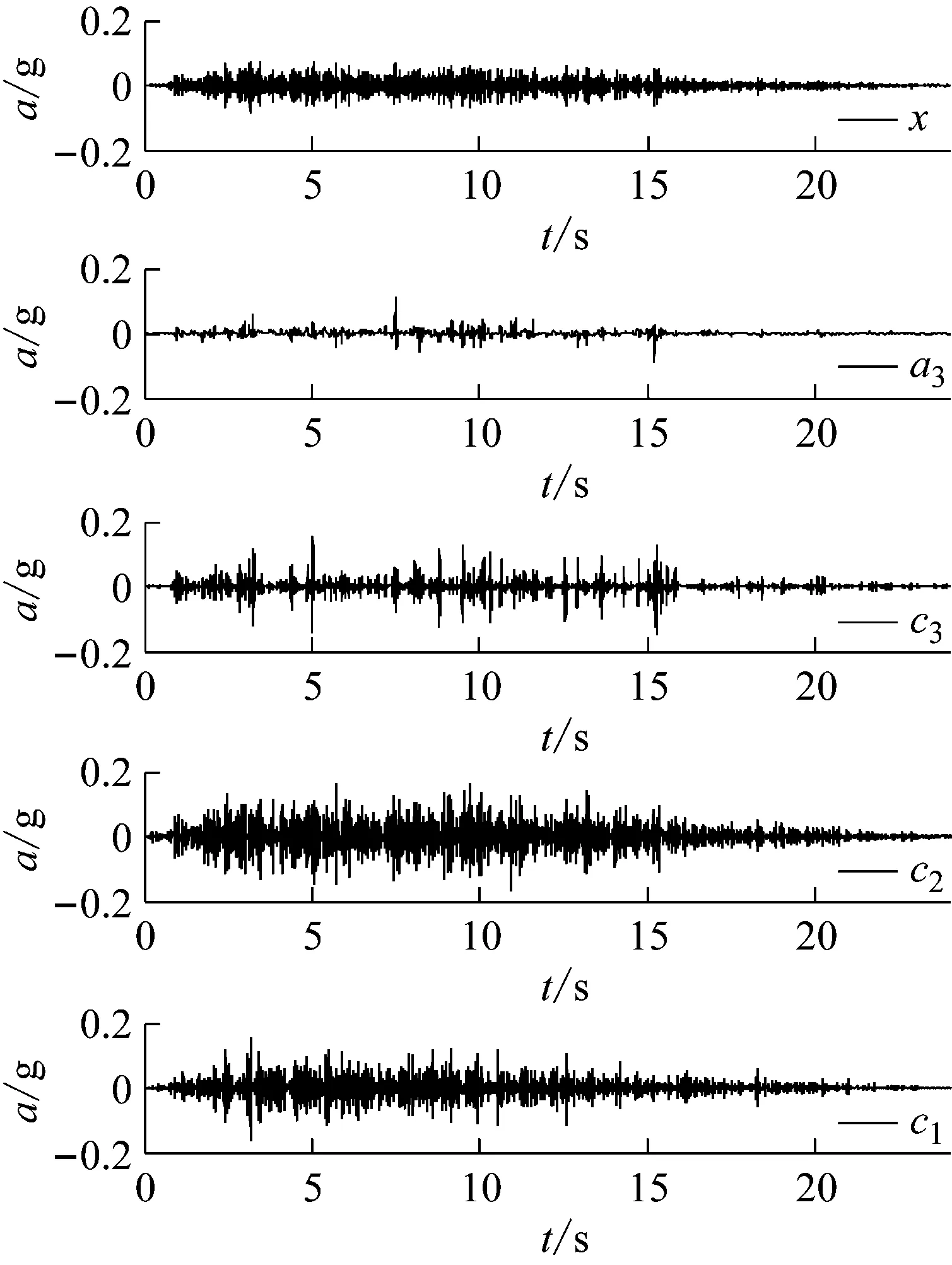
图4 0.55g地震动响应时程信号小波分解Fig.4 Wavelet decomposing of seismic response subjected to earthquake action of 0.55g

2.2 结构初始损伤时刻识别的预警指标

采用小波分析可以获取信号中的突变信息，但是在实际应用中并非所有情况下都可以实现有效识别损伤。因为各种不确定性因素的影响，实际监测信号包含各种扰动引起的突变，如何判断对应于初始损伤实际发生时间的信号突变缺乏定量的判别方法，当前的研究都是基于定性的曲线观察。

为此，本文提出用一个随时间移动的固定大小的时窗来观察任意时间点上信号的突变性的方法，针对小波分解信号，提出了一个基于移动观察窗统计特征的损伤预警指标sk

(4)

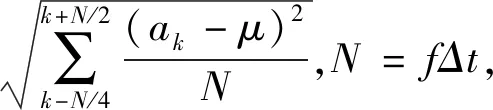
(5)

式中，xk是各时间点τk的响应信号值或小波分解系数。N为τk邻域内的一个观察窗ΔT中所包含的小波分解系数数目。f为采样频率，Δt为时窗大小。xn为观察窗内的所有信号值或小波分解系数的集合。σxn为观察窗内集合组成的样本的标准差。μ为样本均值。

标准差能反映组内个体间的离散程度。用任意时刻的信号值除以观察窗内样本的标准差，更能体现信号的突变程度。一般设定一个损伤预警指标阈值μ，当sk>μ时，即认为结构出现损伤。通常，只有当μ>2时，才能比较明显的观察到信号的突变。

以一段悬臂梁为例说明这一问题及所提出指标的有效性。梁高0.8 m，宽0.2 m，输入随机荷载为y(t)，加载时长为5 s，输入方式为基底输入，结果采样频率为1 000 Hz。

选用具有较高阶消失矩的db6小波作为小波变换基函数，分解次数j=3。图5从左到右分别为损伤云图以及测点1、2的小波图，其中s为测点的加速度响应信号，D为测点的损伤系数，d1为信号小波分解的第一尺度细节信号，DI为损伤指标sk。

本文所采用的损伤系数定义如式(6)所示

(6)

观察图中的小波分解信号d1，可以看出，由于损伤所造成的信号不连续现象并不严重，因此小波分解高频系数并不能对结构的损伤做出有效的预警；但是采用本文提出的基于移动窗的损伤预警指标值sk，可有有效的识别出测点1的损伤时刻为0.41 s，测点2损伤时刻为0.85 s，识别结果与实际损伤D的发生时刻吻合。表明结合小波变换与损伤预警指标sk能对信号的不连续现象给出明确的指示，从而能够精确的识别结构的损伤时刻。

y(t)=sin(25t)+sin(50t)+sin(100t)

(a)损伤云图

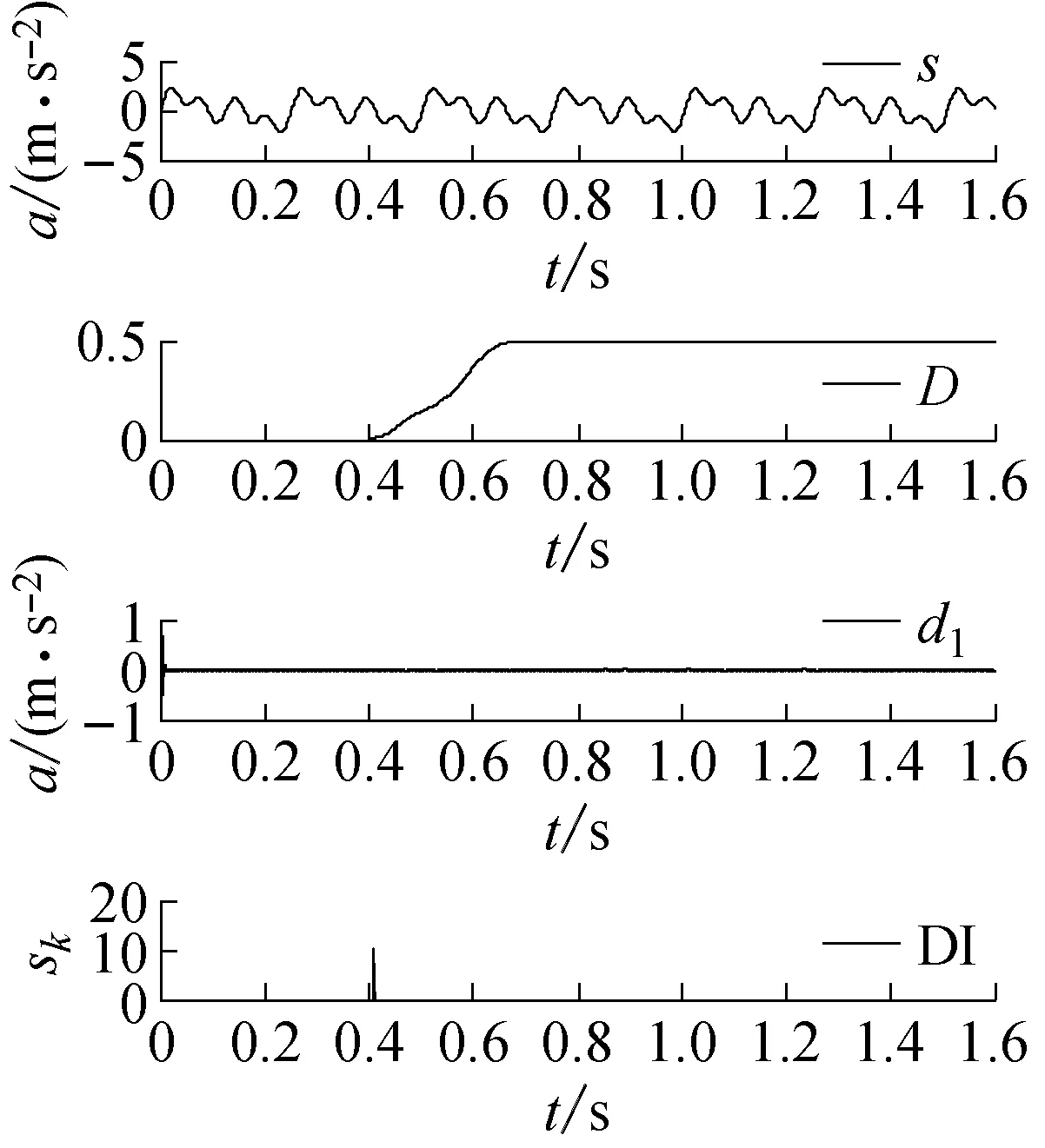
(b)测点1

(c)测点2图5 小波分解与损伤预警指标Fig.5 Wavelet decomposition and damage-alarming index

2.3 方法验证

本文针对振动台模型试验测试结果进行分析。模型施加地震荷载工况1～3分别为峰值加速度0.65g、0.45g、0.25g。坝体损伤部位如图6所示。

重力坝属于大体积混凝土结构，局部损伤引起的结构整体刚度变化很小，很难从结构整体的动力特性变化识别出结构损伤。但是损伤引起的局部非线性变化会导致附近的动力响应出现突变点。提取不同工况下的加速度时程信号，对其进行不同尺度的小波分解。分析损伤状态信号特征，得出损伤时刻。选用具有较高阶消失矩的db6小波作为小波变换基函数，分解次数j=3。得到不同工况下坝体折坡处的加速度分解信号如图7所示。其中，D为测点的损伤系数，d1为响应信号在第一尺度的小波空间上的投影，DI为损伤指标sk。

从图7可以看出，0.65g下初始损伤时刻为1.59s，损伤系数最大为9.2×10-2；0.45g下的初始损伤时刻为1.94 s，损伤系数最大为9.05×10-2；0.25g下加载到2.64 s时出现损伤，损伤系数最大为2.40×10-3。以上初始损伤出现时刻的损伤极小，对坝体整体动力特性几乎无影响。

图6 坝体损伤部位Fig.6 Damage location

三种加速度工况下，在信号的第一层高频系数d1中，都可以观察到突变点，但是0.65g和0.45g工况下，实际初始损伤时刻之前的系数中也有波动，不过幅值较小，对结构的损伤时刻容易出现错误的判断。但是，采用本文提出的基于移动窗的损伤预警指标sk，则可以更为清晰的识别出初始损伤时刻。说明结合小波变换与损伤指标sk能对结构损伤时刻给出较准确的指示。

(a)工况1

(b)工况2

(c)工况3图7 基于小波及预警指标的损伤识别Fig.7 Damage identification based on wavelet decomposition and damage alarming index

3 基于小波变换的结构损伤部位识别

当结构由于损伤而导致刚度降低时，结构的空间域信息会出现细微的间断点。通过对结构的空间域信息进行小波分解，根据细节信号出现奇异点的位置来识别结构损伤发生的位置。

3.1 基于小波的损伤部位识别

假设坝体中上部存在损伤为0.1～0.6的初始竖向缺陷(如图8所示)，计算地震作用下的地震动响应，提取模型1.3 m高程处5 s时刻的竖向变形曲线进行使用具有高阶消失矩的db6小波分析，分解层数为3层。

基于位移的小波分解细节系数如图9所示。从图中可以看出不同损伤工况下小波分解细节系数在单元21处均出现了奇异点，且随着模拟损伤程度的不断增加，奇异性越明显，说明小波分析能够识别结构损伤部位。

对模型1.3 m高程处各测点的加速度响应时程做均方根处理，对加速度均方根进行小波分析，结果如图10所示。从图中同样可以观察到损伤的位置，即使对加速度均方做了平滑处理，其端点处依然存在较大的波动。比较两种响应信息的识别结果，可以看出，基于结构挠度曲线的损伤位置识别结果优于基于加速度响应的。

因此，基于小波分析可以识别出损伤部位。但是，对于此类大体积混凝土结构，无论是基于位移的还是基于加速度的，损伤引起的小波系数波动范围都在损伤部位两侧一定范围内。如果监测点超出这一范围，则结构的响应对局部的微小损伤不再敏感，或者说，监测点对损伤具有局部敏感性。只有当损伤由局部发展到一定程度从而改变结构整体的动力特征，损伤影响才具有全局敏感性。

3.2 不同部位的初始损伤次序识别

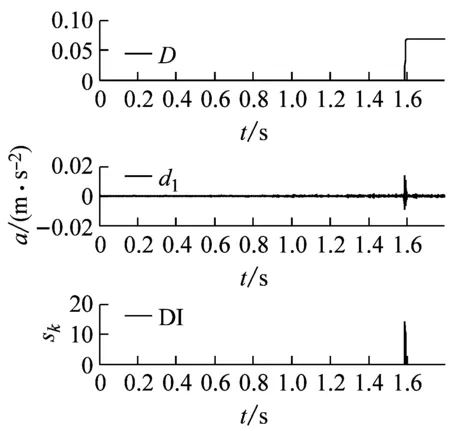
0.65g地震动作用下坝体不同部位初始损伤出现的次序如图11所示，位置1为坝体中段折坡处，位置2为坝头折坡处，位置3为靠近坝底折坡处。

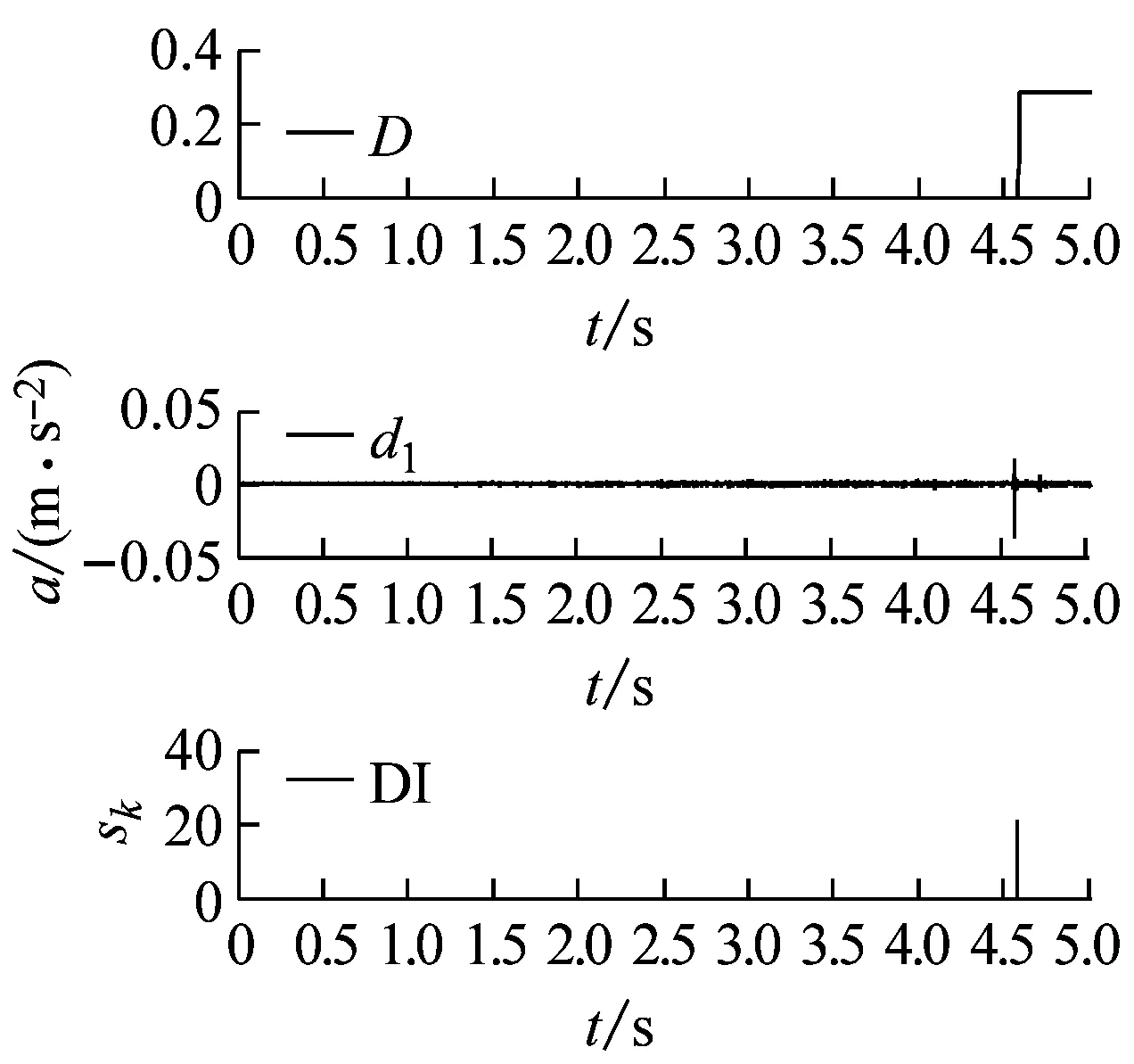
图12为不同位置的小波分解信息及损伤识别结果。从图中损伤系数D的发展曲线可以看出，三个位置初始损伤出现的次序分别为1.59 s、4.58 s和5.30 s。但是，基于db6小波分解得到的第一尺度细节信号d1在实际损伤出现时刻前都有大量微幅波动，而基于定量评估的sk则准确的判别出初始损伤时刻，与数值仿真计算得到的结构相吻合。说明结合小波变换与损伤指标能对不同位置的损伤时刻给出指示。

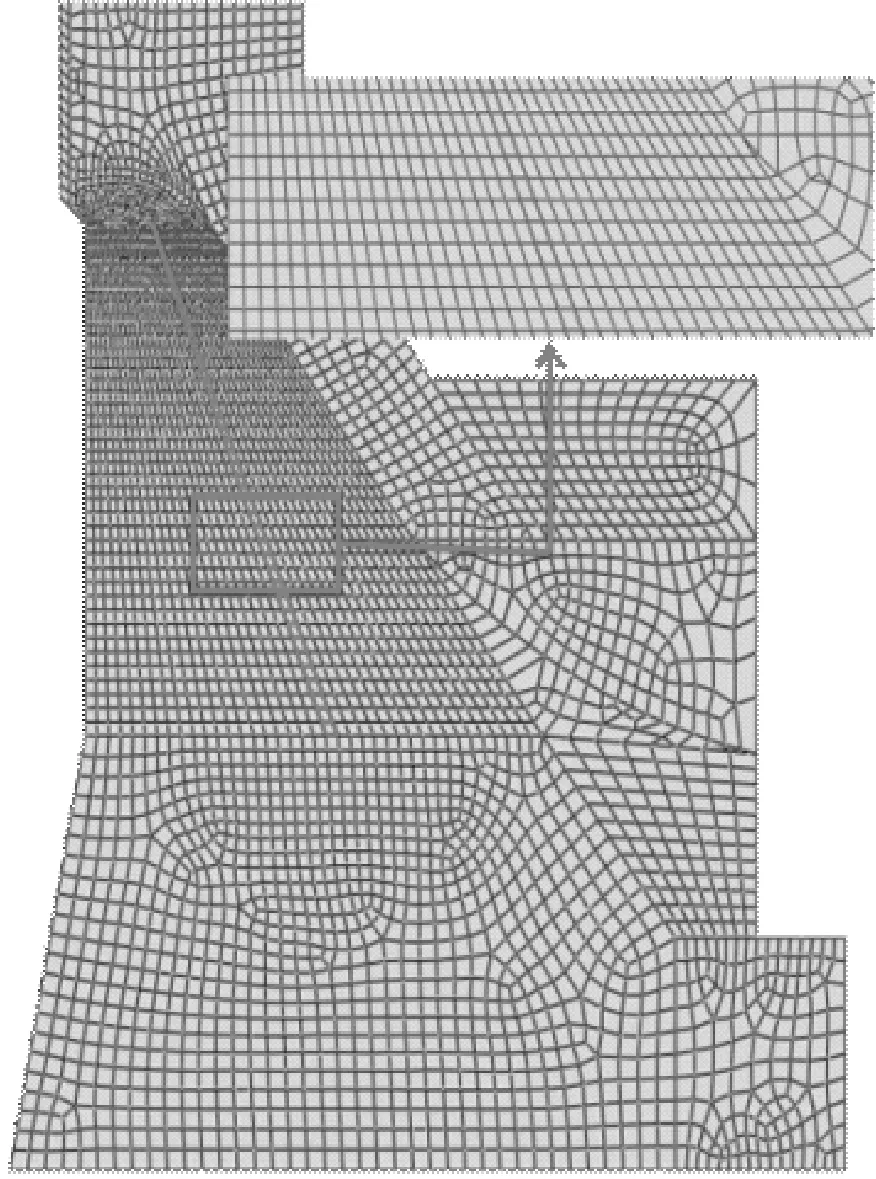
图8 计算模型及内部损伤带Fig.8 FEM model and internal damage belt

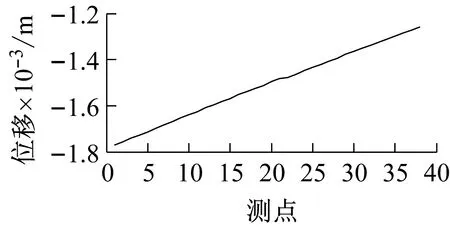
图10 加速度均方小波损伤识别Fig.10 Location identification in terms of acceleration square root

(a)部位1

(b)部位2

(c)部位3图11 坝体不同时刻的损伤部位Fig.11 Damage onset locations of dam

(a)部位1

(b)部位2

(c)部位3图12 不同部位的损伤时刻识别Fig.12 Damage onset time identification of different locations

4 结 论

混凝土坝在强震中的损伤破坏部位和损伤程度的识别对于大坝安全评估很重要，但是大坝损伤发展过程和地震动失效模式的识别同样具有非常重要的价值。基于强震后的脉动激励响应信息不能再现实际损伤的应力状态，并不能得到真实的损伤结果，也不能得到坝体损伤的时间发展过程。必须采取基于强震过程实时响应信息的损伤识别方法。

本文通过振动台试验和数值仿真研究，对于小波识别技术中存在的小波分解系数不能准确的判断损伤时刻突变信息的问题，结合小波分析与数据统计特征，采用更具有物理意义的能够反映观察窗内样本离散程度的标准差，提出了基于移动时间窗的损伤预警指标，分析了局部损伤对于大体积混凝土结构的监测部位的影响范围。结论如下：

(1)当结构某处出现损伤时，表现在响应信号上为一瞬态分量，可以通过小波低尺度信号上的突变峰值识别结构的损伤。由于小波变换对某些损伤识别不敏感，本文提出了一个损伤预警指标sk，并通过对三种地震动工况的损伤时刻的识别以及同一种工况下的三个不同位置的损伤识别，验证了该损伤预警指标的有效性和可行性。

(2)利用小波变换把信号分解为不同频带上的信号值来检测信号的奇异点，通过低尺度极大值出现的位置判断结构的损伤位置。由于小波本身具有振荡性，所以在损伤位置附近的测点上对于大体积混凝土结构的局部损伤也具有一定的敏感性。

本文仅对该问题作了探索性研究，尚有很多需要改进的地方。比如本文所提出的损伤预警指标目前只用于识别损伤时刻，还没有建立损伤指标与损伤程度的关系，有待于深入研究；大体积混凝土结构的地震动损伤在起始阶段其影响是局部的，随着地震动强度的增大，不同部位的损伤对结构响应的影响将互相耦合，损伤指标与地震动强度、测点之间的距离等方面的相关性也需要更进一步的研究。