基于能量有限元法的损伤充液管道振动分析

尚保佑 ，朱 翔，李天匀 ，梁孝天

(1.华中科技大学 船舶与海洋工程学院，武汉 430074；2.船舶与海洋水动力湖北省重点实验室，武汉 430074；3.高新船舶与深海开发装备协同创新中心，上海 200240)

充液管道在工程领域中的运用非常广泛。这些结构在服役期间会出现各类形式的损伤。针对管道结构开展早期的损伤识别研究具有重大的理论意义和实际价值。在结构损伤识别的研究中，基于结构振动特性的损伤识别法成为众多科研人员关注的重点。周祥等[1]对主流的几种损伤探测识别方法进行比较，并简述了目前机械结构损伤识别领域中一些待解决的问题。刘景斌等[2]则在比较各损伤识别方法优劣性的基础上，展望了未来损伤识别方法的发展趋势。

结构中的振动波传播和振动能量的传播通常是结构物理参数，如刚度、质量和阻尼的函数，所以结构物理参数的变化会导致结构振动能量分布的变化。近年来基于振动能量的损伤识别方法得到了较多的关注。

Zhu等[3]对损伤Timoshenko梁和圆柱壳的振动功率进行了分析，提出了利用振动功率流[4]采用一局部转动弹簧来模拟梁中的损伤，同时也利用断裂力学的相关理论得到局部弹簧的转动刚度。Santos等[5]认为结构中的损伤改变了能量耗散的结构，以能量流作为研究的基础，用在研究梁结构的损伤识别和检测中。随后朱翔等[6]采用有限元法对裂纹损伤结构的功率流进行了相关研究并且引入了结构声强的概念,以此实现了结构表面能量分布、传播以及在裂纹位置周围分布的可视化分析。Pang等[7]基于振动功率流理论，以呼吸裂纹板作为研究对象并对其输入功率曲线进行分析。基于能量有限元法，王迪等[8]求解了损伤薄板结构的振动，并以结构声强和能量密度为指标识别板结构中的损伤。能量有限元法(EFEA)是近些年发展起来的一种用于解决结构中高频振动分析的方法[9]。它结合了统计能量法(SEA)和传统的有限元法(FEA)的优点，是一种混合建模分析技术[10]。一方面，子系统可以通过网格的形式表现，另一方面，类似FEA的方法可通过节点描述能量的衰减过程。因此，对于结构的模态没有过多要求，可以涵盖中高频段。Zhu等[11]利用有限元法和能量有限元法相结合的混合方法来预测结构在中频部分的振动，通过算例获得整个系统在不同区域的能量分布，验证了所提出的方法可以用于在中频范围内的振动预测。刘知辉等[12]研究了三板耦合情况下的能量传递系数，并使用多种单元类型和混合单元等方法将能量有限元的应用拓展至任意复杂耦合结构[13]，并分析了由耦合板结构组成的封闭箱体。葛月等[14]研究了任意耦合角度下弯曲波、纵波和剪切波入射时特定入射角度下的能量传递系数，分析了耦合板结构中耦合角度、耦合板厚度、激励频率对能量传递系数的影响。解妙霞等[15]对能量有限元在复合材料结构动响应中的相关研究进行综述。

国内外学者针对充液管道的振动开展了大量的研究。Tijsseling[16]对充液管道系统的流固耦合研究进展进行综述。王琳[17]研究输流管道的稳定性与非线性动力学机理，对管道的稳定性、分岔、混沌等特性进行了分析。包日东等[18]通过在模态空间展开运动控制微分方程的方法，分析了输流管道振动系统的非线性动态响应。Luo[19]等利用微分求积法计算弯曲管道的非线性动力响应，阐述了微动磨损对管道损伤的影响。Zhou等[20]研究轴向功能梯度悬臂输流管的线性动力学问题。

从查阅文献来看，目前尚未有文献建立充液管道结构振动分析的能量有限元方程，也没有基于能量有限元法的充液管道结构损伤识别研究。本文首先推导建立了充液管道的能量有限元方程，然后基于能量有限元法对含有损伤的充液管道结构的振动特性进行分析。分别采用传统有限元法和能量有限元法对管道中的能量密度进行了计算，验证本文能量有限元法的正确性。通过分别改变含损伤充液管道中损伤部分的刚度、阻尼。计算充液管道在损伤前后的能量密度和能量流，并分析损伤参数与能量流之间的关系。

1 充液管道的能量有限元方程

1.1 充液管道的能量平衡方程

由文献[21]可知，输流管道的运动控制微分方程为

(1)

当不考虑管内流体流速带来的影响即μ=U=0、P=T=0时，输流管道运动方程退化为充液管道运动控制微分方程

(2)

式中：Ip是管道的截面惯性矩,Ep是管道材料的杨氏模量，ρp、Sp分别是管道的材料密度和横截面积，ρf、Sf分别是管内流体的材料密度和横截面积，η代表管道结构阻尼，w(x,t)表示管道的径向位移，F代表激励的幅值，δ代表狄拉克函数，x代表管道的轴向坐标，x0是激励作用的位置，ω是圆频率，t表示时间。

假设方程的通解为

w(x,t)=(A1e-ikfx+A2eikfx+A3e-ikfx+A4eikfx)eiωt

(3)

式中：A1、A2、A3、A4为由边界条件、连续条件等确定的待定系数。kf为复波数。若有η<<1,可得如下表达式

(4)

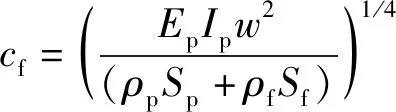
管道的势能密度和动能密度分别表示为

(5)

(6)

管道的总能量密度为其势能密度和动能密度之和，因此管道的总能量密度可以表示为

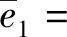
(7)

式中：k1、k2分别表示为复波数kf的实部和虚部，即有关系式，kf=k1+ik2。

Wohlever等[22]已经证明，在高频计算时，含有A3、A4的近场解可以忽略不计，此时能量密度的平稳远场解的表达式为

(8)

在管道的振动模型中，弯曲波功率流通常是由剪力和弯矩携带传递，剪力所对应的功率为

(9)

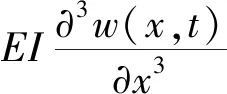
弯矩所对应的功率为

(10)

管道中能量流的平稳解表达式

(11)

比较式(8)和式(11)，可得出远场能量流与远场能量密度的梯度成正比关系

无恒产而有恒心者，惟士为能。若民，则无恒产，因无恒心。苟无恒心，放辟邪侈，无不为已。及陷于罪，然后从而刑之，是罔民也。焉有仁人在位罔民而可为也？是故明君制民之产……然后驱而之善，故民之从之也轻。今也制民之产……此惟救死而恐不赡，奚暇治礼义哉？[4](P211)

(12)

式中，cgf=2cf代表弯曲波的群速度。

取一个管道单元进行分析，能量密度随时间的变化应为管道单元的入射功率与耗散功率之差，可以通过以下表达式[23]得出

(13)

式中：Πin为管道单元的输入功率；Πdiss为管道单元的耗散功率。

由于结构内的耗散能量与能量密度存在如下的关系式[24]

(14)

联立式(12)、式(13)、式(14)，不考虑外界输入的管道单元的能量平衡方程为

(15)

考虑外界输入则

(16)

1.2 充液管道的能量有限元方程

采用Galerkin加权残值法对上述方程进行求解，可以得到如下的加权残值方程表达式[25]

(17)

(18)

为了表述方便，可将式(18)写成矩阵的形式

[Ke]{ee}={Pe}+{Qe}

(19)

式中:[Ke]表示每个单元含单元刚度和质量的系数矩阵;{ee}则是需要求解的能量密度向量;{Pe}是在节点处输入的激励向量;{Qe}表示每个单元两端能量流的进出。

通过求解式(19)，即可计算得到节点的能量密度，进一步可得到每个管道单元的能量流。

1.3 损伤充液管道的能量有限元计算

当结构中出现损伤后，损伤区域的动力学参数如刚度、阻尼等都会发生变化，从而引起结构中振动能量的变化。因此，基于能量有限元法得到损伤结构的能量流特性和变化特性，从而也可为损伤结构的损伤识别提供依据。

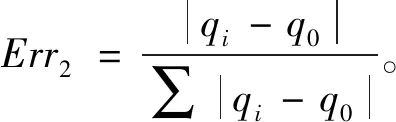
两种损伤指标都是基于能量有限元法，在后文中将采用能量有限元法对含损伤单元的充液管道的能量密度和能量流进行计算。

2 不同工况下损伤充液管道结构的振动能量分析

2.1 管道结构能量有限元法准确性验证

在第1节中推导得到了充液管道的能量密度方程和能量有限元方程，为验证所建立的充液管道能量有限元方程的正确性，本文将能量有限元法(EFEA)解得到的能量密度和传统有限元(FEA)解的结果进行对比分析。选取一段充液管道，管道两端固支，管长L为1 m，外径Ro为10.5 mm，内径Ri为8 mm，管壁材料密度ρp为7 800 kg/m3，管壁杨氏模量E为210 GPa，阻尼系数η为0.02，管内流体单位长度质量mf为0.2 kg/m，管内流体密度ρf为980 kg/m3。在管道中心处输入一激励功率为2.7×10-4W，激励频率为8 000 Hz的激励力。参考能量密度值取为1×10-13J/m。其中，EFEA模型划分单元数为10，形函数取n=3的Lagrange插值函数，如图1所示。

有限元模型在ANSYS Workbench中建立，其中FEA模型中模拟管道的三维体单元共58 798个，如图2所示，流体单元18 706单元，如图3所示。设置流固耦合属性，并求解在简谐激励下的稳态响应。

图1 能量有限元模型示意图Fig.1 Energy finite element model

图2 常规有限元管道单元网格划分图Fig.2 FEA grid plot of pipe element

图3 常规有限元流体单元网格划分图Fig.3 FEA grid plot of fluid element

需要注意能量有限元模型和传统有限元模型的网格划分原则不同，传统有限元由于捕捉频率较高的振动响应时，单元尺寸小，网格规模大。而能量有限元方法求解得到的能量密度是对时间和空间进行平均之后得到的相对平滑的解。因此可将传统有限元法计算得到的各节点处位移解，按照其本身波长选取合适的长度进行局部平均，得到与能量有限元法计算对应的节点处能量密度值。将两种方法求得的能量密度进行对比，得到充液管道沿着管道长度方向分布的能量密度图，如图4所示。

从图4中，EFEA得到的各节点能量密度分布与FEA得到的各节点能量密度分布吻合较好，从而验证了本文建立的充液管道能量有限元方程的正确性。这为后文分析损伤管道的振动特性提供了基础。

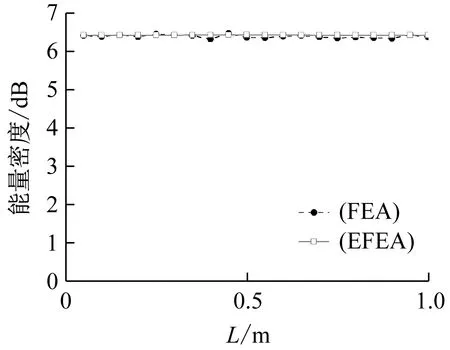
图4 两种方法沿管道长度方向能量密度分布的结果对比Fig.4 Energy density distribution along the pipe length

2.2 损伤充液管道的振动分析

2.2.1 损伤单元刚度变化对振动能量的影响

当管道等结构中出现损伤时，其损伤部位的局部刚度一般会减小。在本节中假设损伤仅引起局部刚度减小。

与前述算例类似，将管道分成10个单元，并按管道长度方向进行编号，如图5所示。其中受损单元编号为6(标深色)，假设该单元损伤后的弹性模量分别降低1%、5%和10%。按照能量有限元法求解损伤前后管道的能量密度和能量流。

图5 管道的损伤模型Fig.5 Energy finite element model of damaged pipe

当损伤单元的弹性模量降低5%时，图6给出了能量密度变化的损伤指标Err1沿着长度方向的分布图。

图6 管道的损伤指标Err1分布(E=0.95E0)Fig.6 Damage index Err1 distribution (E=0.95E0)

由图6可知，基于能量密度变化得到的Err1，在受损单元的节点处变化比较明显，在损伤一侧的能量密度变化值会产生突变。这是由于波传播在经过损伤位置时由于结构不连续出现扰动和不连续的结果，因此可根据管道结构节点的能量密度变化情况来识别管道的损伤位置。

同时也计算出管道中的能量流，从而得到第二种损伤指标并进行分析，如图7所示。

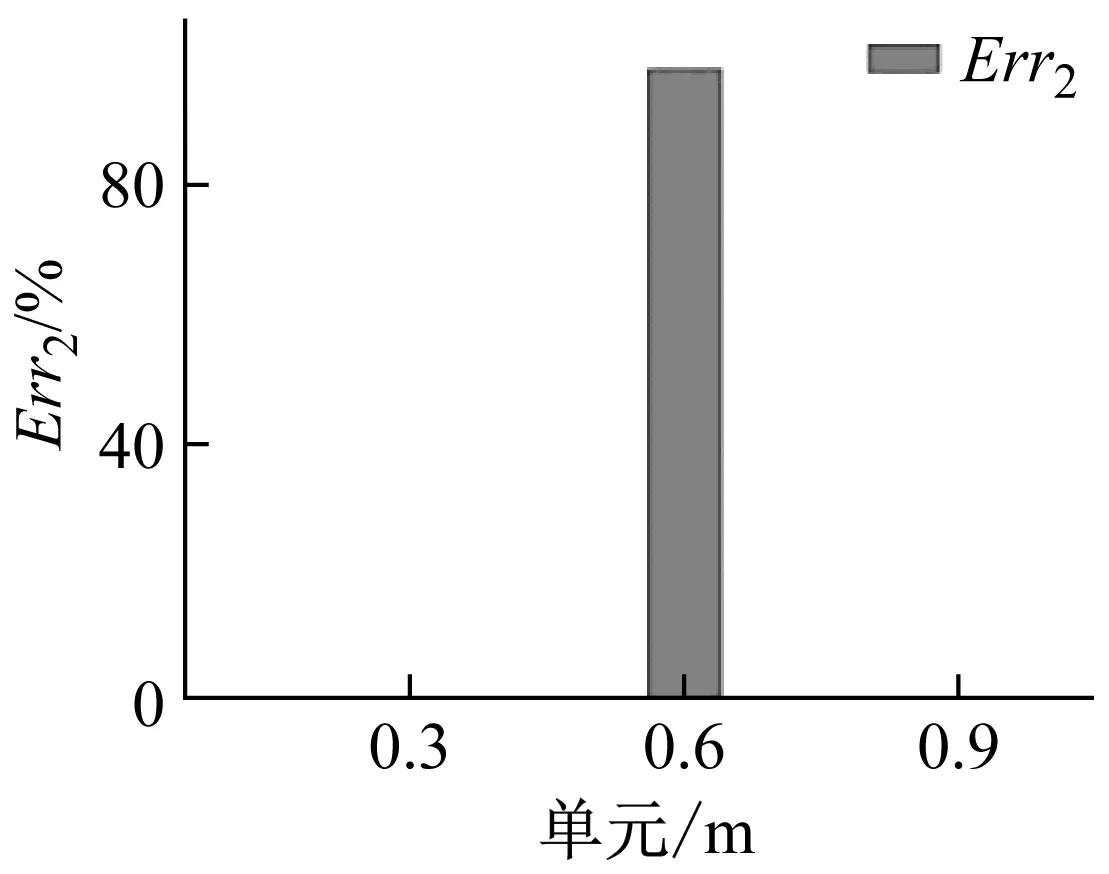
图7 管道的损伤指标Err2分布(E=0.95E0)Fig.7 Damage index Err2 distribution (E=0.95E0)

从图7中看出，Err2在受损6号单元处表现明显，可以直观的反映出受损单元，因此可由管道结构的能量流变化情况来识别管道结构的损伤位置。

将损伤单元的弹性模量分别减小1%、5%和10%，结构的损伤采用能量流前后的差值表示，即Δq=|qi-q0|，如图8所示。

图8 不同刚度变化情况下管道能量流差值比较Fig.8 Damage index Δq of different stiffness

从图中可见随着损伤单元刚度变化幅度的增加，管道单元能量流差值变化也更加明显，并且都在损伤单元处达到峰值。

2.2.2 损伤单元阻尼变化对振动能量的影响

本算例中假设损伤仅引起局部单元的阻尼增大。假设算例中损伤单元的阻尼分别增大1%、5%，采用能量有限元法计算充液管道的能量密度和能量流。图9给出了损伤单元阻尼增大1%时，Err2的分布图。图10为损伤单元取不同阻尼值时的能量流差值。

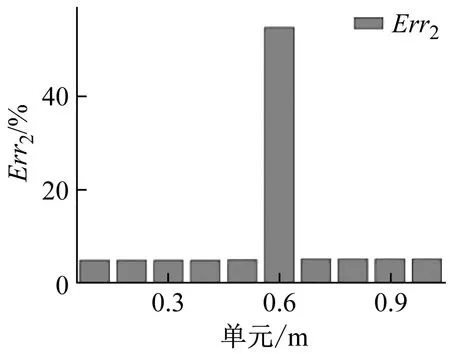
图9 管道的损伤指标Err2 分布(η=1.01η0)Fig.9 Damage index Err2 distribution (η=1.01η0)

从图9中看出，当某个单元的阻尼发生变化时，会引起周围能量流明显的突变，同样可以清晰地识别出充液管道的损伤部位，从图10中看出，随着损伤单元的阻尼增大，损伤前后管道中能量流差值会有明显的上升。表明损伤引起的阻尼变化越明显，管道能量流的变化也越明显，从而可以反映损伤的程度变化。

图10 不同阻尼变化情况下管道能量流差值比较Fig.10 Damage index Δq of different damping

3 结 论

本文基于能量有限元法对含有损伤的充液管道的振动特性进行了分析。推导得到了充液管道的能量有限元方程。将EFEA的方法同传统的有限元FEA的结果进行了分析和验证，表明本文建立的充液管道的能量有限元模型的准确性。

在验证管道能量有限元方法合理性的基础上，将其应用于分析损伤管道结构中，通过管道单元的弹性模量的减小和阻尼的增大来模拟结构损伤的程度，利用能量有限元法计算充液管道中单元的能量密度和能量流。通过分别建立基于能量密度和能量流的两个损伤指标，发现两种损伤指标都可以表征出损伤位置，其中能量流差值对管道结构的损伤更为敏感。

与传统的基于振动的损伤识别方法相比，本文提出的方法避开了繁琐的模态参数求解，且对结构微小的缺陷十分敏感，有一定的优势。但应用到实际工程中，还需要进一步深入研究。