基于粒子群优化算法的光纤陀螺温度误差分段补偿方法
佟 林,覃方君,冯卡力,黄春福,王 智
(海军工程大学 电气工程学院,武汉 430033)
光纤陀螺由于具有精度高、寿命长、动态范围大、对重力加速度不敏感等优势[1],已经广泛应用到导航的很多领域,有着良好的发展前景和研究价值[1-2]。
由于光纤陀螺内部构造的原因,光纤陀螺对温度很敏感,温度漂移成为主要的误差源[3],所以研究光纤陀螺的温度特性,得到温度补偿模型对提高导航精度是非常重要的。文献[4][5]利用多项式法进行温度建模,文献[6][7]利用神经网络进行温度建模,以上方法都是采用单一模型进行补偿,忽略了光纤陀螺温度误差的复杂性。基于此,文献[8][9]提出了分段建模的补偿方法。本文基于分段建模思想,以大量的实测数据为基础,分析陀螺的温度误差特性后,提出了基于粒子群优化算法的光纤陀螺温度误差分段补偿方法。
本文方法的核心是确定最优补偿函数。文献[9]的分段多模型补偿方法(后文称传统方法)仅考虑温度单方面影响,利用最小二乘法求取补偿函数,精度受限。近年来随着人工智能的迅速发展,神经网络已经逐渐被应用到各个领域[10]。1995年Kennedy 和Eberhart 提出了粒子群优化算法(Particle Swarm Optimization,PSO算法)。本文在光纤陀螺温度误差建模时同时考虑温度以及温度变化率,利用PSO 算法进行模型参数的极值寻优,求得最优补偿函数。
1 温度和温度变化率影响机理
光纤陀螺中有许多对温度敏感的光学材料和器件,在不同的温度下工作时它们的性能是不同的,这样就会影响陀螺的输出,产生温度误差。根据光学Nyquist 定律,当温度在绝对零度以上时,光纤折射率将产生热涨落,引起光纤中的相位变化。特别是随着光纤长度的增加(光纤长度超过2 km 时)和环境温度的升高,这种因温度产生的相位噪声甚至超过散粒噪声,最终限制光纤陀螺的检测阈值。温度相位噪声在光纤圈长度较短的中低精度光纤螺中可以忽略,但在惯性导航级高精度光纤陀螺中,温度产生的噪声也是必须要考虑的问题。
当两束干涉光分别以顺时针(CW)和逆时针(CCW)方向在长度为L、折射率为n的光纤环传输时,产生的相位延迟分别为:
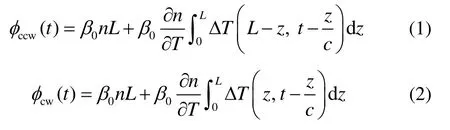
式中,φcw(t)为顺时针光沿光纤环传输产生的相移;φccw(t)为逆时针光沿光纤环传输产生的相移;β0为光在真空中的传输常数,其值为2π/λ,λ为光波长;n为光纤折射率;c为光在光纤环中传播的速度;z为任一点到端点的距离;ΔT为光纤环z点处的温度分布变化量。式(1)减去式(2)后积分得:

式中,c0为光在真空中的速度。
将式(3)分为两部分积分(0,L/ 2)、(L/2,L) ,得:

当温度变化率改变时,内部光纤环的温度场会随着变化,从而使光纤环内部膨胀和折射率不均匀,从而对通过光纤环反向传播的两束干涉光产生的影响不同,产生非互易相移。式(4)继续整理得:
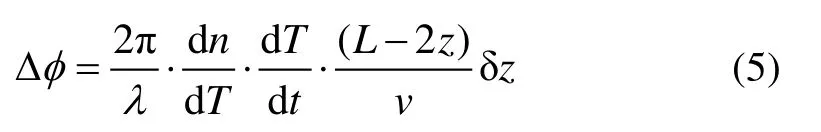
由式(5)也可以得出结论,引起相位误差的因素中,温度变化率的影响至关重要。
2 基于PSO 算法的建模补偿
通过前一节的分析发现,陀螺漂移不仅与温度非线性相关,而且与温度变化率也非线性相关,进而本文在传统模型的基础之上[9],加入了温度变化率影响因子,模型通式为:
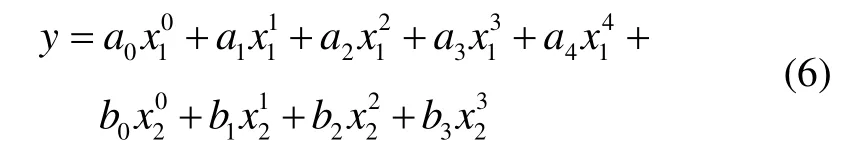
其中,a0、a1、a2、a、3a4表示与温度有关的参数,b0、b1、b2、b3表示与温度变化率有关的参数,x1表示温度,x2表示温度变化率,y表示温度误差。
为了求出式(6)中模型未知的补偿系数a0、a1、a2、a3、a4、b0、b1、b2、b3,本文采用PSO 算法进行极值寻优来求解。与其它群体智能优化算法一样,PSO 算法得到的最优解是在寻优空间中通过群体中不同粒子之间的相互竞争合作来搜索得到的[11]。
本文温度补偿方法的核心为使用PSO 算法确定最优补偿函数,步骤如下:
Step 1:初始化。首先将一群均匀分布在指定的寻优空间中的粒子初始化,即在某个范围内随机给定每个粒子的初始速度和位置。寻优空间即为要补偿的温度区间,每个粒子都表示寻优的一个潜在最优解,即每个粒子位置代表一组补偿系数,适应度、位置和速度是PSO 算法表示粒子特征的三项指标。
Step 2:确定适应度函数F。实验采集得到的数据经过处理后得到真实的温度漂移,作为训练样本将式(6)得到的预测温度漂移作为训练样本剩余误差表达式为ε(i) =Y(i) -y(i),其中i为当前陀螺采样数。将每一次采样的剩余误差的平方和作为本模型适应度函数:

Step 3:根据粒子初始位置计算每一个粒子的适应度值,并将它作为该粒子的个体极值,所有个体极值中最优的设置为群体极值。
Step 4:根据个体极值和群体极值,更新粒子的速度和位置。更新公式为:

其中,ω为惯性权重,c1和c2为非负的常数称为学习因子,r1和r2为分布于0 到1 之间的随机数。
Step 5:更新个体极值和群体极值。根据更新后的粒子位置计算每一个粒子的适应度值,并与原来的个体极值Pidk进行比较,若优于则更新此值,新的所有个体极值中最优的设置为新的群体极值。
Step 6:进行迭代运算。不断重复Step 4 和Step 5,设置迭代次数k,满足条件后停止搜索,此时粒子位置为模型的系数a0、a1、a2、a3、a4、b0、b、1b、2b3。将其带入式(6)中即得到温度补偿模型。
Step 7:设置PSO 算法的基本参数,这些参数的优劣将直接影响到最终的寻优结果:
1)种群规模:种群规模为Step 1 中粒子的总数,此参数根据经验确定,经过大量的试验,结合本模型实际情况种群规模设置为400。
2)迭代次数:迭代次数的选择根据模型和精度要求的改变而改变,太少会使结果精度达不到要求,太多不仅会大大延长算法的时间,而且还会出现迭代过饱和现象使精度反而降低,通过大量的试验反复验证最终确定此模型的迭代次数为300 最佳。
3)粒子的速度和位置范围,位置范围为Step 1 中的寻优空间即温度区间,设定为问题空间的10%~20%[12]。
4)惯性权重ω,表示粒子当前速度多大程度上继承原来的速度,ω较大便于全局搜索,较小便于局部搜索,为了平衡两种搜索能力,根据光纤陀螺温度补偿的特殊性,本文采用线性递减惯性权重。

其中,ωstart为初始惯性权重,k为当前迭代数,ωend为最大迭代数时的惯性权重,kmax为最大迭代数。
5)学习因子c1和c2:分别调节向个体和全局最优方向飞行的最大步长,若c1为零,粒子将陷入局部最优,没有处理复杂模型的能力,若c2为零,将得不到全局最优解。标准的PSO 算法中c1=c2= 2。
本文针对光纤陀螺温度补偿的特殊性对粒子群算法进行改进,采用一种带收缩因子的PSO 算法的参数设定方法,引入了收缩因子K,使速度更新公式变为:
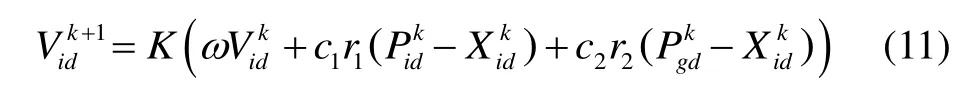
解出c1=c2=1.494 45。本模型采用此数值作为PSO 算法的学习因子进行寻优运算。
综上,总结得出本文PSO 算法极值寻优流程图如图1所示。
上述步骤即为温度误差建模全过程,极值寻优得到的最优粒子群即为式(6)中全部的未知系数,将其带入式(6)得到最优补偿函数y,此函数即为该温度区间 的温度误差补偿模型。
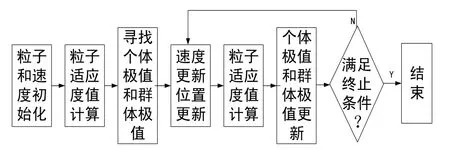
图1 算法流程图 Fig.1 Algorithm flowchart
3 试验验证与结果分析
将光纤惯导系统置于温箱内,惯导系统的3 轴按东北天方向放置,温箱和惯导均保持静止,使光纤陀螺仅受到地球自转的激励,保持温箱温度为-15℃,待陀螺输出稳定后逐渐升温10 h,温度升至50℃,测量-15℃~50℃温度区间变化时的陀螺数据,陀螺采样频率为200 Hz。然后对数据进行处理,得到各个温度下的陀螺漂移,结果如图2所示。
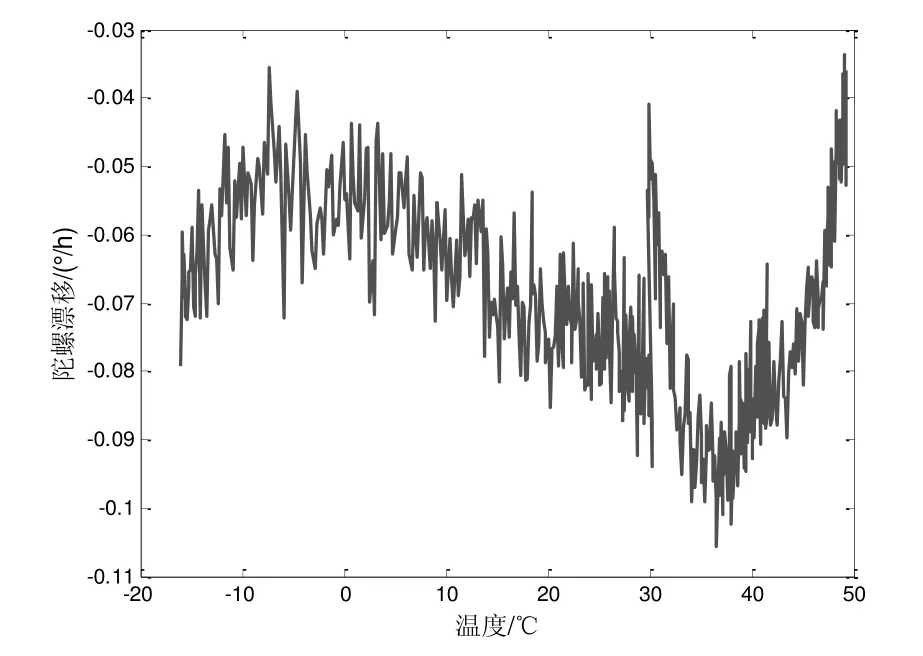
图2 陀螺漂移 Fig.2 FOG drift
通过对图2中实测数据误差特性进行分析发现,在以下5 个温度区间,温度误差曲线总体上保持单调趋势,所以本文将温度分成这5 个区间进行补偿。5 个温度区间分别是:-15℃~0℃;0℃~15℃;15℃~30℃;30℃~37℃;37℃~50℃。
最后,使用本文方法进行温度建模,结果如表1所示。 将表1所得的系数分别带入相应的温度区间进行补偿,补偿结果如图3所示。

表1 本文方法补偿系数 Tab.1 Compensation coefficients of the proposed method
从图3可以看出,本文所建模型能够较好地拟合温度误差曲线。求取补偿后剩余误差的均值和标准差得:在整个温度区间-15~50℃内,补偿前漂移的均值为-6 .90 ×10-2(°/h),标准差为 1.5317 ×1 0-2(°/h);本文方法补偿后剩余误差的均值为 -2.9621×10-5(°/h),标准差为6.6524 ×1 0-3(°/h)。表2为传统算法的补偿结果,可以得出:补偿后剩余误差的均值为 1 .1209 ×1 0-4(°/h),标准差为 6.9597 ×1 0-3(°/h)。

图3 补偿效果 Fig.3 The effect of compensation

表2 传统方法的补偿系数 Tab.2 Compensation coefficients of traditional algorithm
通过以上分析可以得出:相比补偿前,本文算法补偿后陀螺零偏稳定性降低了56.57%,零偏均值减少了99.96%,补偿效果非常显著;相比传统方法,本文方法补偿后陀螺零偏稳定性降低了4.42%,基本保持不变,零偏均值减少了78.55%,近一个数量级,说明本文方法可以大幅度降低漂移均值效果优于传统算法。
为了进一步验证本文方法补偿效果,使用同一个惯导系统按照原方案重新采集-15℃~50℃的实测数据,为了验证本文补偿系数适用于其它的温度变化率,验证试验采用与原试验不同的温度变化方式,使温度变化率不同。继续使用本文模型进行补偿以验证模型效果,如图4所示。
将此结果与传统方法和未补偿时进行比较,各个温度区间陀螺漂移的均值和标准差如表3所示。可以看出,在-15℃~50℃温度区间内,相比补偿前,无论零偏均值还是零偏稳定性均明显降低。相比传统算法,零偏稳定性基本保持不变,而零偏均值有了明显降低,降低了1 个数量级,与前文结论一致,说明本文方法确实可以提高补偿效果,并在降低零偏均值方面明显优于传统方法。
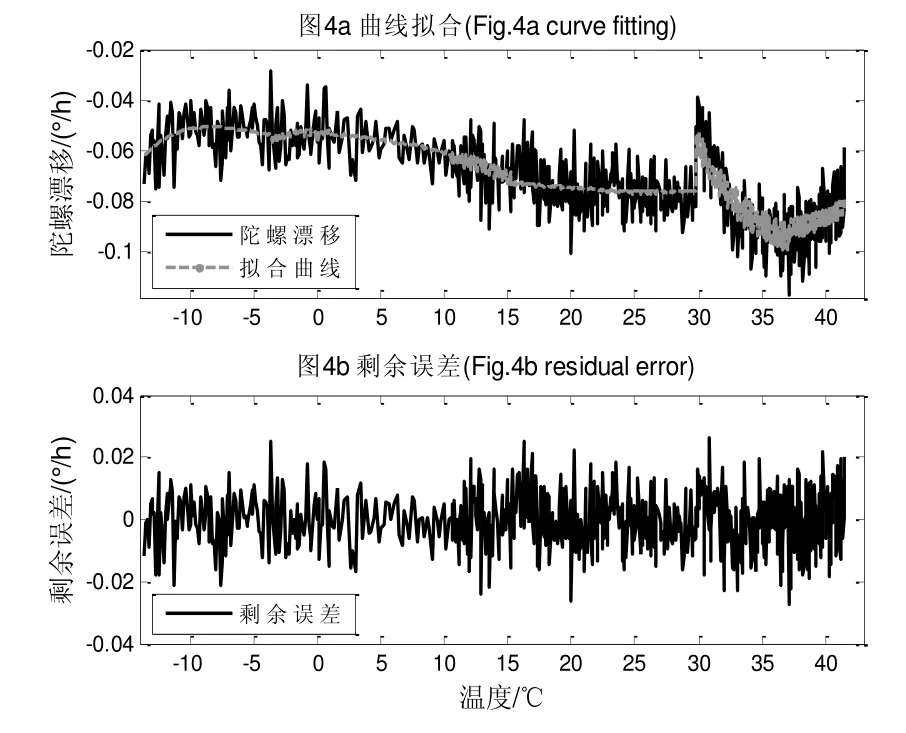
图4 补偿效果验证 Fig.4 Verification of compensation effect
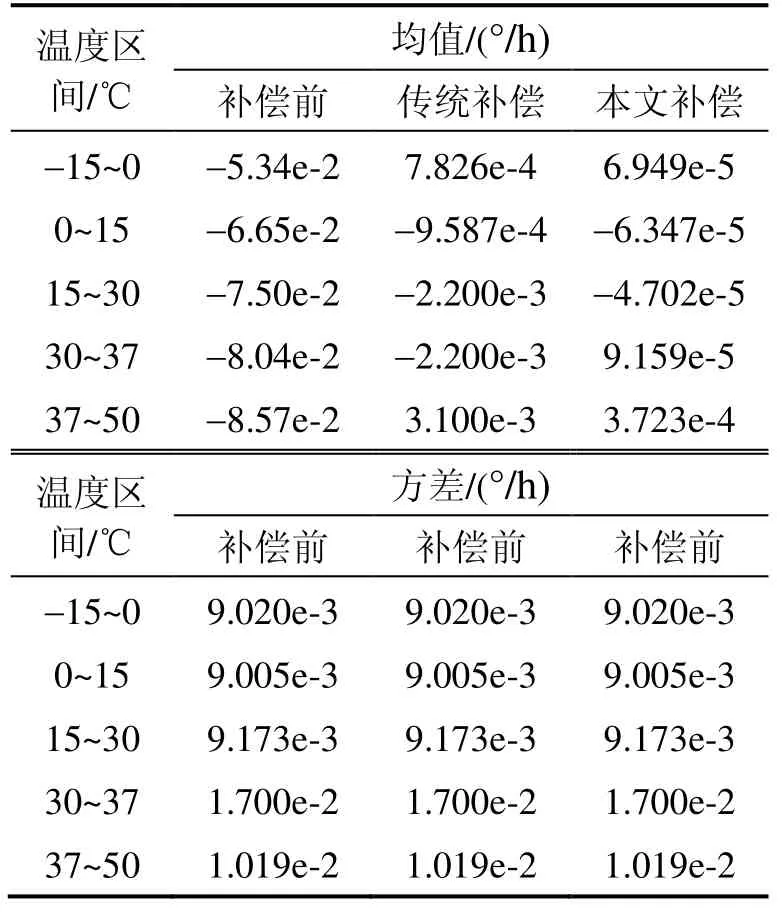
表3 误差比较 Tab.3 Error comparison
4 结 论
本文在实测数据分析处理基础上,提出了基于粒子群优化算法的光纤陀螺温度误差分段补偿方法,在建模时加入温度和温度变化率影响因子,并引入PSO 算法极值寻优。试验结果表明,本文方法在补偿温度误差方面效果显著,并在降低零偏均值方面明显优于传统方法。重新采集数据进行验证,得到了相同的结论。
在寻优得到补偿系数后,带入可得到温度误差补偿方程,只要光纤惯导提供实时的温度数据,就可以计算出实时的温度变化率,通过方程即可得到实时的温度误差补偿值,所以本文方法可以对温度温差进行实时补偿,具有较好的应用广泛性和工程实用价值。

