室内环境下基于边际约束的快速路径自主探索算法

徐晓苏，梁紫依，杨 博，王 迪

（1.微惯性仪表与先进导航技术教育部重点实验室，南京 210096； 2.东南大学 仪器科学与工程学院，南京 210096）

目前移动机器人已经在工业、农业和军事等各领域取得了广泛的应用，减轻或者取代了人类繁重的劳动。从搜索和救援到行星探测和监视，自主探索技术也发挥着越来越重要的作用[1]。移动机器人与环境交互，根据传感器数据构建完整可靠的环境地图即移动机器人自主探索[2]。大规模环境下，人为引导进行环境探索，工作量繁琐且巨大；在地震、火灾等危险环境中，人类无法直接进入，只能依赖机器人携带的传感器实现对环境的自主认知和建模。因此，移动机器人对未知环境的自主探索就变得尤为重要。如何在短时间和路程完成移动机器人所在环境的遍历，从而得到足够空间环境用于全局地图创建，是自主探索的核心问题。自主探索是机器人实现真正自主的关键性一步，也是机器人技术的一个重要研究方向[3]。

移动机器人自主探索算法的研究一直受到国内外众多学者的关注。在自主探索的过程中，机器人需感知环境来获得一系列的局部目标点，指导机器人进行环境的全局遍历。1997年，Yamauchi[4]提出了前沿探测（frontier exploration）理论，将已知区域与未知区域的交界定义为前沿，探索过程中使机器人尽可能驶向未知区域，但是该算法忽略了其他环境因素的影响，不能保证每一步都能获得新息。2015年，P.G.C.N.Senarathne 和Danwei Wang[5]提出了一种计算高效的增量式边界检测方法安全可达边界检测，降低了边界生成算法的计算量，同时提高了执行效率。2016年，坦佩雷理工大学 Lauri[6]等人提出了基于地图信息采样的正演探索算法，在以激光测距仪（Laser Range Finder,LRF）观测环境信息构建的地图的基础上，根据移动机器人运动速度、观测范围等约束，将探索过程描述成部分可观测马尔可夫决策过程（Partially Observable Markov Decision Process,POMDP），通过对局部环境信息进行采样，从而推演当前目标点，并结合基于边界的启发式探索策略，有效规避了局部最优问题。2017年，南开大学的于宁波[7]等人提出了一种基于RGB-D 信息的移动机器人自主探索与地图构建方法，将探索过程描述成部分可观测马尔可夫决策过程，结合局部地图推演策略与全局边界搜索策略,建立了移动机器人的自主探索方法，但是该算法对于全局的路径规划仍没有具体的说明。

自主探索策略几乎可以简化为寻找和移动到下一步最佳探索目标点[8]。因此，路径规划是机器人技术的重要研究方向，也是实现移动机器人在探索目标点之间移动的关键技术。传统的路径规划算法有人工势场法、A*算法、D*算法等。近年来，越来越多的现代智能算法被提出，例如模糊逻辑算法、神经网络算法、群智能启发式优化算法[9]等。由于快速扩展随机树算法具有随机性和高维度适用的特点，基于该算法的各种改进方法逐渐应用到高维复杂环境的路径规划中[10-12]。

综上，上述自主探索方法都侧重于探索目标点的确定，解决了机器人探索目标点的确定问题，但是忽略了具体的路径规划部分，或者耗费高成本寻求最优的路径。本文针对上述问题，从机器人移动范围和运行时间考虑，提出一种基于边际条件约束的启发式路径自主探索算法。首先将机器人探索问题描述为POMDP 过程，然后结合边际约束条件的快速扩展随机树（Rapidly-exploration Random Trees,RRT）算法寻找路径，再采用启发式算法优化路径，进而提出一种基于边际条件约束的启发式快速路径自主探索算法。

1 移动机器人自主探索问题建模

基于移动机器人当前位姿与构建的地图信息进行推演，衡量探索过程中的信息量，确定探索目标点，是探索算法的研究重点。由于实际环境通常是部分可观测和时变的，移动机器人通过激光测距仪、深度相机等传感器观测到的环境具有不确定性，因此机器人在未知环境中进行自主探索需要对这些因素进行考虑。根据传感器观测范围和机器人移动速度、动力学等条件，在传感器构建的局部地图上，我们可以把移动机器人自主探索问题描述为POMDP 过程，并用 〈τ,S,U,Z,Ts,O,R〉进行描述，其中：

●τ= ｛0 ,1,… ,k,…｝ 表示一次探索任务确定目标点经历的决策阶段。

●S=X×M表示机器人的隐藏状态，包括地图状态M和机器人的内部状态X。在实际环境中，M和X都是可观测的。

●U表示机器人的动作集合，即按照动力学、运动学等约束，机器人可以执行的动作。

●Z表示状态空间的观测集合。

●TS表示状态转移模型，由机器人状态转移TX和地图状态更新TM共同组成。

●O表示观测模型，采用光线追踪模型对栅格占据地图进行采样，得到当前状态的观测值。

●R表示奖励函数，由状态信息S，观测信息Z和动作集U共同构成。

奖励函数R是评价路径好坏的准则，本文采用互信息[8]作为对路径信息增益的度量。表达式如下：

其中，b表示当前的置信状态，u表示当前的动作序列，x′、m′分别表示从机器人内部状态和地图状态采集的样本。

若假设机器人内部状态和地图状态的变化过程是 独立的，并且其中N是 采样数，则可将式(1)近似为：

根据互信息的链式规则证明，当N→∞，其收敛于I(X,M;Z|B,U)。

式(2)中，第一部分为移动机器人位姿的期望信息增益。考虑室内环境的地形平整性，机器人能平稳地进行移动。因此，可以假设机器人的运动模型不存在噪声，表述为

式(4)所示为机器人速度运动模型的具体形式，其中以机器人位姿状态与观测值表示的互相关函数值为0。

第二部分表示的是地图状态的期望信息增益，为地图和观测值的互相关函数值，通过对当前地图推演前后指定范围内栅格的熵值求和实现积分运算。在2D的栅格占据地图中，每个网格具有两个隐藏的状态：占据和空闲。栅格的具体状态具有不确定性，用p表示栅格的占据概率，则p∈[ 0,1]，其中1 表示占据点即存在障碍物，0 表示空闲点[13]。采用二元信息熵的形式来表示每个栅格的信息量：

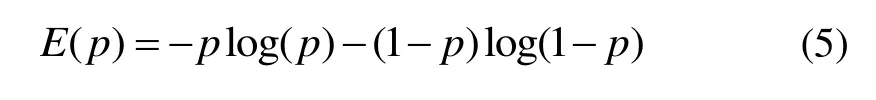
2 基于边际条件约束的启发式自主探索算法

RRT（Rapidly-exploration random tree）算法最早在1998年的美国爱荷华州立大学被提出。该方法通过随机搜索自由空间，逐渐构建一棵从初始状态到目标状态的可达路径的随机树。在迭代过程中，随机生成采样点并搜索距离该点最近的树的顶点，然后以确定步长生长，得到该方向上的新节点，并检查其是否属于安全环境，直到到达目标点[14]。RRT 算法是概率完备的，且在搜索全局性、随机性等方面具有优势[15]。

借助RRT 算法的快速性，参考文献[15]的动态窗口形式，本文提出一种基于边际条件约束的启发式自主探索算法。一方面限制随机树采样点的生成范围，弱化随机性；另一方面，将随机树的节点类比二维坐标系的原点，平行于地图的长和宽方向，构造四个象限，根据节点和目标点的象限方位，确定随机点采样的象限。同时，采用启发式评估函数[16]对移动路径进行优化，避开障碍物的同时，尽可能地减少机器人的旋转动作和缩短移动路径的长度。

在室内环境中，每一次探索目标点的确定和传感器的选取及其观测范围、机器人的速度运动模型等有关系。现有的自主探索大多是通过激光雷达等距离传感器对环境进行感知，获取障碍物的位置。因此探索给出的目标点一定是在同一个空间，即起点和终点之间的边界内始终存在可连通的区域。

基于该情况，基于边际条件约束的启发式自主探索算法改进步骤如下：

首先，基于传感器观测到的已知地图，由于起点q_start和终点q_goal位于图中，并且在大多数情况下，起点q_start和终点q_goal围成的边际窗口远小于实际探索的全局地图，因此将采样的范围限制在该边际窗口中。

其次，将随机树上距离终点q_goal最近邻节点q_gnear设置为起点q_start。同时，保持边际窗口的大小不变，将其移动至新起点处。

然后，根据二维坐标系的四个象限的概念，以起点q_start为原点，平行于初始地图的长和宽为相互垂直的两坐标轴。根据终点q_goal的方位，确定边际窗口的相应象限。

接着，在边际窗口中进行概率采样。给每一个采样点赋予随机的概率值p_rand，设置一个概率阈值p_thre。当大于阈值时，在边框窗口中产生采样点，否则以终点q_goal为采样点。

最后，当找到起点q_start和终点q_goal的可达路径后，采用启发式评估函数对路径进行优化[16]，寻找起点q_start到第一个无碰撞连接的路径节点。循环如此，直至终点q_goal。

图1是构造边际窗口的示意图。其中，黑色的五角星为起点，红色的五角星为终点，黑色细实线即为初始设置的采样边际窗口。

图1 边际窗口示意图 Fig.1 Marginal window diagram

若q_start= [xs,ys]，q_goal= [x g,yg]，则边际窗口的四条边应满足以下条件：

图2中的红色三角形为随机采样点，黄色线条是随机树节点的连接线。在图2中，由于起点和终点围成的边际窗口在起点的第四象限，因此在起点的第四象限的边际窗口中根据随机赋予的概率值进行采样。图2为一随机采样结果。根据随机树节点位置，重新设置红色三角形为起点，终点仍然在起点的第四象限，因此将边际窗口移动，但保持窗口大小不变。采样点和终点的象限关系可以根据式(7)进行判断。

图2 节点象限示意图 Fig.2 Node quadrant diagram

在基于边际条件约束的启发式自主探索算法中，若在边际窗口的移动过程中，碰到障碍物或地图边界时，用该边界限制边际窗口。在基于该算法使用受到限制时，放松边际条件的约束，在全局空间进行采样。这样不仅一定程度限制了采样空间的大小，减少采样点的数量。而且随着随机树T的生长，边际窗口进行窗口式的滑动，增加了路径生成的可能性，缩短了程序运行的时间，提高了算法的效率。

最后采用启发式评估函数寻求最优的路径节点。将算法找到的路径节点记为

其中，h为启发式评估函数。

基于边际条件约束的启发式自主探索算法的具体操作步骤如下：

步骤1：初始化起点q_start和终点q_goal，并将起始节点q_start作为快速扩展随机树T的根节点；

步骤2：判断起点q_start和终点q_goal是否相同，且起点q_start和终点q_goal的连接线是否不和障碍物发生碰撞，若是则转入步骤8；

步骤3：根据起点q_start和终点q_goal构成的边际窗口重新设置采样空间。初始时，最近邻节点q_gnear为起点q_start；

步骤4：根据节点q_gnear和终点q_goal的方位关系，即确定终点q_goal位于最近邻节点q_gnear的哪一个象限。在该象限中以边际窗口为范围生成随机的采样点q_rand。

步骤 5：给每一采样点随机赋予一个概率值p_rand，当p_rand小于设定的概率阈值p_thre时，设置采样点q_rand为终点q_goal，否则为随机采样点q_rand；

步骤6：根据设定的步长q_step，沿着节点q_near和采样点q_rand的连线方向生成一个新节点q_new，若新节点q_new和节点q_near的路径不与障碍物碰撞，则新节点q_new添加到RRT 树T中，并将其设置为q_near，否则舍弃，重新进入步骤4；

步骤7：判断新节点q_new是否为终点q_goal，或者终点q_goal是否在RRT 树T的新旧节点连接线上。如果条件成立，则将最后一个树节点设置为终点q_goal，否则重新进入步骤3，直至找到终点q_goal；

步骤8：返回起点q_start和终点q_goal的路径，并记录为path；

步骤9：找到路径初始点p_start和path上不发生碰撞的最后一个节点p_free。然后重新设置其后的一个节点为起始点p_start，直至终点q_goal；

步骤10：返回最终起点q_start和终点q_goal优化后的路径；

步骤11：程序结束。

具体的算法流程图如图3所示。

图3 基于边际条件约束的启发式自主探索算法流程图 Fig.3 Flow chart of heuristic autonomous exploration algorithm based on marginal condition constraint

3 仿真实验

本文的仿真实验分为两个部分:POMDP 探索算法仿真实验和本文提出的基于边际条件约束的启发式自主探索算法的验证。

3.1 POMDP 探索算法仿真实验

在以LRF 观测环境信息构建的地图基础上，根据移动机器人运动速度、观测范围等约束进行预测，衡量探索过程中的信息量进而生成目标点是POMDP 探索模型的主要思想。具体的推演过程包括粒子采样、权重计算与重采样。

初始时，根据机器人底盘转速范围进行均匀采样， 生成可能的粒子动作序列，并为每个粒子分配权重。当粒子多样性小于设定值时，进行重采样。然后依据粒子具体数目和迭代的次数进行滤波，算法逐渐收敛于最优粒子的动作序列。

图4是在Ubuntu16.04 下机器人操作系统（Robot Operating System,ROS）中运行的实验结果图。图中黑色线条是已知区域和未知区域的边界，黑色的圆是移动机器人模型，灰色区域是已知区域，深灰色区域是未知区域。绿色线条即是移动机器人可能的粒子动作序列，经过多次迭代计算后，逐渐收敛于子图(c)中的最优粒子的动作序列。

图4 POMDP 探索算法仿真实验 Fig.4 Simulation experiment of POMDP exploration algorithm

3.2 基于边际条件约束的启发式自主探索算法

本算法的仿真实验是在 Windows 10 下的MATLAB-R2015b 上进行。图5是RRT 算法的结果图。

图5 RRT 算法 Fig.5 Rapidly-exploring Random Trees algorithm

在图5的(a)(b)(c)(d)四幅子图中，黄色线条表示RRT 算法产生的路径，黑色线条表示经过启发式优化算法优化之后的路径。从图中可以看出，由于路径是在全局空间基于随机采样生成的，所以随机树的节点数量存在明显的差异。复杂情况下，树节点数量几乎遍布全局，如图5(a)所示；简单情况下，树节点数量较为适量，如图5的(b)(c)(d)子图。图5的(a)(b)(c)(d)子图是传统RRT 算法随机产生的四个结果图，在大量的实验中，结果相差更为明显。

将本文提出的算法在相同的环境中进行验证。

图6 基于边际条件约束的启发式自主探索算法 Fig.6 Heuristic autonomous exploration algorithm based on marginal constraint

在图6中，黄色线条表示基于边际条件约束的启 发式自主探索算法产生的路径，黑色线条表示经过启发式优化算法优化的路径。与图5相比，图6的树节点数量明显减少。图6的(a)(b)(c)(d)子图的节点数量分别为22、19、26、20，比图5中最少树节点子图(c)还少6 个节点。对比8 个子图规划的路径可以明显看出，经过启发式算法优化之后，机器人的移动路径节点减少，即转角变少，路径移动距离缩短。

在图5和图6的仿真环境中，设置起点、终点和障碍物等环境条件相同，分别运行传统RRT 算法和本文算法，将运行时间结果列于表1中。

表1 RRT 算法和本文算法的时间对比表 Tab.1 Time comparison of RRT algorithm and the proposed algorithm

根据表1的数据可知，启发式优化算法的优化时间很短，对于本文算法和RRT 算法的运行时间几乎不会产生影响。在子图6(c)中，虽然本文算法运行时间稍长于RRT 算法，但和图6的(a)(b)(d)子图相比，本文算法仍具有时间优势。从4 幅子图的运行时间分析，本文算法的时间稳定性优于RRT 算法。

为了验证基于边际条件约束的启发式自主探索算法的实用性，从不同的环境进行验证。

图7 不同环境的基于边际条件约束的启发式自主探索算法 Fig.7 Heuristic autonomous exploration algorithm based on marginal condition constraint in different environments

从图7的结果中可以得出，不管是对于规则还是不 规则的障碍物，改变起点或者终点的位置都不影响本文算法的效果。图7中随机树节点和运行时间都有明显的效果，尤其对于局部较为空旷的空间，效果更为好。

由于采样算法具有一定的随机性，为了验证本文算法的效果不是随机产生的。在相同的环境、相同的起点和终点等环境条件下，分别连续运行文本算法和RRT 算法各30 次，记录运行时间和随机树节点数量，将其统计于图8中。

图8 RRT 算法和本文算法的对比图 Fig.8 Comparison on RRT algorithm and the proposed algorithm

图8的(a)(b)子图中，红色的均是RRT 算法的数据，蓝色的是基于边际条件约束的启发式自主探索算法的数据。从图8(a)和8(b)的对比中可以看出，基于边际条件约束的启发式自主探索算法在运行时间和采样点方面有较好的效果，在随机树节点的对比中尤为明显。根据30 次实验数据统计，RRT 算法的运行时间的均值为2.0289 s，标准差为4.5574，节点数量均值约110 个，标准差为135.6839。而本文算法的运行时间均值为0.4625 s，标准差为0.8447，节点数量约为23 个，标准差约为3.1156。在本次试验中，节点数量减少约80%，时间效果缩短约75%。然而，由于RRT算法的标准差过大，时间和节点数量的效果不能简单用均值代替，多次实验产生的实际效果可能会有些许波动。但是从图形中仍可明显看出，本文算法在时间和节点数量上的性能都有提高，同时，算法的稳定性也强于RRT 算法。

图9是基于边际条件约束的启发式自主探索算法在ROS 下的仿真实验结果。红色的线段是经过基于边际条件约束的启发式自主探索算法给出的路径。从图中可知，本文算法能够适用于探索算法，使得机器人在室内未知环境中实现安全、快速的移动。

将机器人探索的POMDP 模型和基于边际条件约束的启发式自主探索算法结合即可实现机器人的自主探索。

图9 基于边际条件约束的启发式自主探索算法ROS 仿真实验图 Fig.9 ROS simulation experiment of heuristic autonomous exploration algorithm based on marginal condition constraint

4 结 论

室内未知环境下的移动机器人自主探索是实现机器人智能化和自主化的重要部分。本文提出一种基于边际条件约束的启发式机器人快速路径自主路径探索算法，能实现在未知环境下自主探索室内环境。同时，在启发式算法的指导下，优化机器人移动的路径，使得机器人能快速、安全地移动到探索算法确定的下一目标点。采用本文提出的算法能优化多转角路径对机器人带来的不利影响，并且一定程度上节省了程序运行时间，这对于探索任务来说是有重要作用的。