基于摆扫成像的无人机视觉侦察航迹规划方法

李文广，李建增，胡永江，李永科，褚丽娜

（陆军工程大学 无人机工程系，石家庄 050003）

视频侦察是指通过无人机平台搭载的可见光摄像机、红外前视仪等视频载荷，进而获取任务区域内情报数据的一种侦察方式[1]。通过后端对视频数据进行拼接[2]、目标识别[3]、目标定位[4]等处理，可为战场态势分析提供有力的情报支持。但现阶段针对视频侦察任务的航迹规划算法没有考虑视频载荷的摆扫规律及成像特点，导致侦察时存在覆盖盲区和效率低的问题。因此研究基于摆扫成像的无人机视觉侦察航迹规划方法具有重要的现实意义。

XU 等[5]先利用单元分解法对已知区域进行分割，然后将区域覆盖问题转化为旅行商问题，以遍历所有分解单元。该方法能够解决任务区域内含障碍物的覆盖航迹规划问题，但单元分解法对于区域的分割处理会使得算法的未覆盖率实际值偏高，降低侦察效率。SCOTT 等[6]提出遮挡感知航程点生成算法，找到区域内最佳成像点，然后将成像点分配问题转化为车辆路径规划问题，实现区域覆盖航迹规划。但该方法只考虑了载荷成像的分辨率要求，没有考虑整个任务的覆盖要求。AVELLAR 等[7]以单机的最小覆盖时间为依据对区域进行划分，然后利用混合整数线性规划问题解决多机覆盖问题。该方法能够使得侦察覆盖时间最短，但没有结合具体任务背景及覆盖率的要求。徐博等[8]以飞行距离和多余覆盖率为指标，研究了不同飞行方向下，如何规划无人机的最优作业航线，但没有考虑具体任务方式下的成像模型及成像规律，忽略了载荷成像规律对于覆盖策略的影响。

上述算法针对区域视频覆盖侦察问题进行了创新与改进，但仍存在以下问题：1）未结合具体的任务要求及载荷工作模式；2）忽略了载荷摆扫规律对覆盖策略的影响；3）算法的未覆盖率有待优化。针对以上问题，本文提出了基于摆扫成像的无人机视觉侦察航迹规划方法，并进行了理论证明和实验验证。

1 视频摆扫成像模型

对于无人机执行视频侦察任务，应结合视频载荷的摆扫成像模式，来制定相应的航迹覆盖策略。建立视频载荷的摆扫成像模型，研究视频载荷的摆扫周期性成像规律，可为制定航迹覆盖策略提供有效依据。

视频摆扫成像是指视频载荷在垂直于飞行方向上以一定角速度做周期性摆动，完成地面侦察成像的过程[9]。视频摆扫成像过程如图1所示。

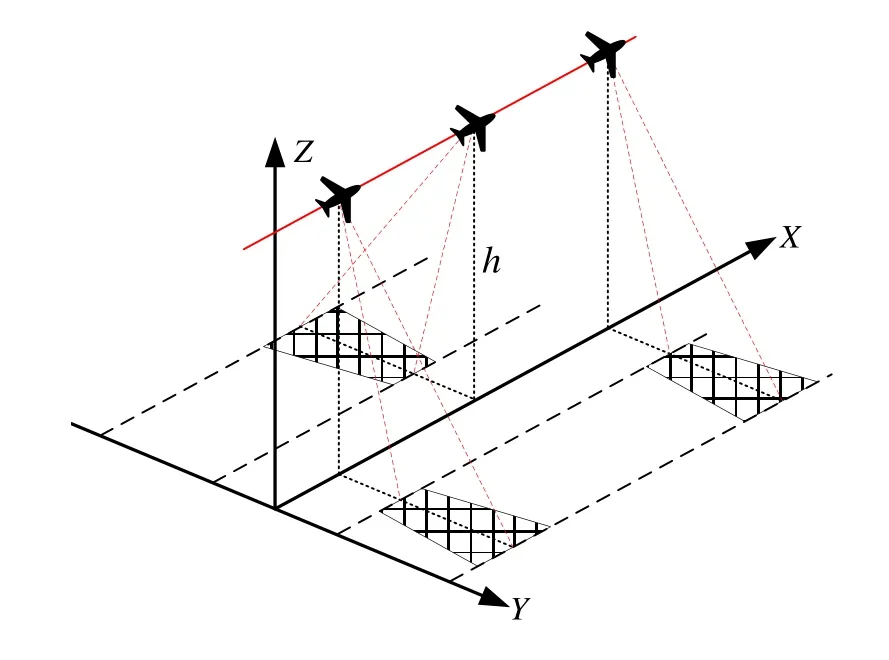
图1 视频摆扫成像过程 Fig.1 Video sweep imaging process

1.1 成像面积计算

由于视频载荷的复合运动比较复杂，为简化计算，所以可做出如下合理假设：

1）定义载荷垂直对地的方向为0，向机身左侧摆动的角度为正，右侧为负，摆动的起始位置为θ= 0；

2）机身左右侧摆动的最大角度相同，且摆动角度的取值满足 -9 0° ＜θ＜ 90°。

计算单位周期摆扫面积方法如下：

步骤1以(0,0,0)点为坐标原点，无人机航向为x轴，机翼右侧为y轴建立辅助坐标系，并求得θ=0时视频帧的5 个点坐标值。当θ= 0时，视频载荷垂直对地，其视频帧成像如图2所示。

图2 视频帧成像 (θ = 0) Fig.2 Video frame imaging (θ = 0)

由光学成像知识可得，视频帧5 点坐标分别为：

其中，h为无人机飞行高度，α为航向视场角的一半，β为纵向视场角的一半。

将这5 个点经坐标变换，转到载荷坐标系下（载荷坐标系的原点是无人机平台上载荷安装位置，坐标轴方向同辅助坐标系）。坐标变换式为：

其中，(a,b,c)为载荷安装位置坐标；a是以坐标(a,b,c)第一分量a所构成的1 × 5矩阵；同理，b、c也是以对应坐标值所构成的1 × 5矩阵。

步骤2载荷摆动任意角度，对应视频帧的5 个点坐标是以B中5 个点坐标进行坐标变换得到的(绕x轴旋转)。假设载荷摆动角度为θ（θ的正负遵循右手定则），则对应的5 个点坐标为：

步骤3将载荷坐标系下的点经坐标变换，转到飞机坐标系下（飞机坐标系原点是无人机位置，坐标轴方向同载荷坐标系）。坐标变换式为：

其中，d、e、f的值取决于无人机位置和载荷安装位置之间的位移差；d是以d所构成的1 × 5矩阵，同理e、f是以对应坐标值构成的1 × 5矩阵。

步骤4已知航向角σ，将飞机坐标系进行旋转操作，使得飞机坐标系转到真实航向位置。

设无人机位于On，北极点位于N，地心为Oe，那么

联立式(4)～(6)，可解得τ。那么将飞机坐标系绕z轴旋转τ-σ(° ) ，可转至真实航向位置。对应视频帧点坐标变换如式(7)所示：

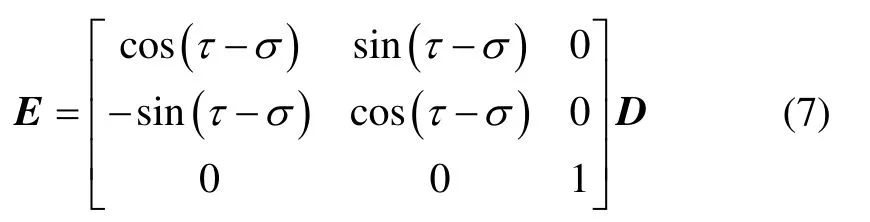
若考虑无人机的横滚角η、俯仰角φ、偏航角δ对于成像的影响，则视频帧的点坐标变换如式(8)所示。

步骤5求视频帧在地面上的真实点坐标。

由无人机位置坐标及F中的5 个点坐标，可求得5 条直线方程l1、l2、l3、l4、l5。然后求解5 条直线和椭球面的交点，即为视频帧在地面上的真实坐标（地球近似为椭球面）。椭球面方程如式(9)所示：

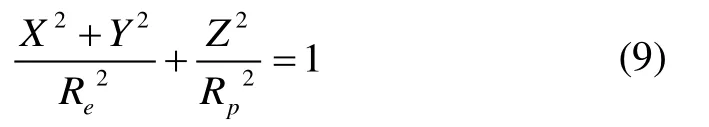
其中，Re为地球长半轴长，Rp为地球短半轴长（2008年7月1日起，我国启用2000 国家大地坐标系，则Re的长度为6 378 137 m，Rp的长度为6 356 752.314 14 m）。

步骤6周期摆动下成像面积的计算。

设摆扫角度范围为 -ω1～ω1，摆扫角速度为ω，帧率为n，一个摆扫周期时间为T，无人机的飞行速度为v。

1）第一个0.25T

载荷摆扫时间：t1=ω1ω；视频总帧数：n1=ω1nω；相邻帧时间间隔：T1= 1n；相邻帧的航向位移：

设F1为第一帧的点集，FN′如式(11)所示：

其中，FN为每帧点集，FN′为考虑航向位移后的点集。

2）第二个0.25T

第二个0.25T与第一个0.25T对应角度下的多边形是相等的，两者之间存在位移关系。假设第一个0.25T的最后一帧是第二个0.25T的第一帧，则Fk如式(12)所示：

3）最后，可利用几何Merge 算法求得周期内所有视频帧围成的不规则多边形面积。

步骤7对不规则多边形进行近似处理。根据视频帧的位置关系，求得内接矩形的长、宽。

1.2 命题及证明

随着视频载荷的摆扫运动，若视频帧之间不存在重叠，则会导致最后围成的不规则多边形成像范围内存在非连通区域，导致侦察盲区及未覆盖率高的问题。所以要对摆扫成像范围内是否存在非连通区域的条件进行讨论。

命题：设无人机的飞行速度为v，一个摆扫周期时间为T，帧率为n。只有当vT＞ 4htanα时，视频摆扫覆盖区域不连通，存在成像盲区。

证明：一般情况下，视频载荷帧率在25～30 帧/s，或者更高可达60 帧/s。所以相邻视频帧之间的时间间隔很小，相邻帧之间的成像范围不存在盲区。故只需考虑第一帧和第0.5Tn帧之间是否存在盲区即可（第一帧是θ=0 时的视频帧）。

当两帧重叠率为0 且无盲区时，有式(13)所示关系：

所以，当vT＞ 4htanα时，两帧之间存在盲区，即视频摆扫覆盖区域不连通。证毕。

注：1）由于相邻帧之间的时间间隔很小，近似认为相邻两帧在航向上存在水平位移。2）步骤4 进行坐标旋转是为了确定无人机的初始姿态，以便下一步考虑无人机横滚、俯仰、偏航姿态对于成像的影响，且要严格按照式(8)的坐标旋转变换的顺序计算。3）命题成立的前提条件是第一帧和第0.5Tn帧重叠率为0且不存在盲区。实际从视频拼接的角度，两帧之间应该要满足一定的重叠率，才能满足后端视频拼接的要求。4）只要第一帧和第0.5Tn帧不存在盲区，那么任意摆扫周期成像范围内都不会有盲区。

2 基于视觉成像的区域分割

覆盖航迹规划（Coverage Path Planning,CPP）是指在满足某种性能指标最优的前提下，规划出一条能够遍历覆盖区域的最优飞行航迹[10]。常见的覆盖航迹规划方法有栅格法[11-13]和扫描线法[14-16]。而基于视觉侦察的区域分割首先利用扫描线法规划得到航带参数，然后用各航带实际成像范围对覆盖区域进行分割。但是由于视频摆扫的成像特点，有以下三种情况：

Case 1:当2htanα＜vT＜ 4htanα时，航带实际成像范围长度要小于航带长度，且航带长度和成像范围长度的差值为： ΔL= 2(0.5vT-htanα)。

证明：由命题可知，为了保证视频摆扫覆盖区域不存在成像盲区，必须要满足vT＜ 4htanα，即证不等式右边。

根据各视频帧的位置关系，对不规则多边形成像范围取内接矩形时，矩形的长与左右摆动最大角度时的视频帧位置有关。矩形的宽所对应的两条边分别由第一帧和第0.5nT帧的位置关系及第n(t- 0.5T)帧和第nt帧的位置关系确定。

图3 成像范围小于路径代价 Fig.3 Imaging range is less than path cost

当vT＞ 2htanα，矩形的宽对应视频帧的位置关系如图3所示。航带长度和成像范围长度的差值L如式(14)所示：

由图3可知，实际成像范围在O1O n之间。证毕。

Case 2:当vT= 2htanα时，航带实际成像范围长度要等于航带长度，且航带长度和成像范围长度的差值为： ΔL=0。由Case 1 同理可证。此时，矩形的宽对应的视频帧位置关系如图4所示。

Case 3:当vT＜ 2htanα时，航带实际成像范围长度要大于航带长度，且航带长度和成像范围长度的差值为： ΔL=-2 (htanα- 0.5vT)。

由Case 1 同理可证。此时，矩形的宽对应的视频帧位置关系如图5所示。

图4 成像范围等于路径代价 Fig.4 Imaging range equals path cost

图5 成像范围大于路径代价 Fig.5 Imaging range is greater than path cost

注：1）考虑整数周期的视频摆扫范围，且近似取内接矩形，可以简化区域分割的分类情况；2）航带成像范围的宽就是内接矩形的宽，但不等于航带间距。

3 航迹规划步骤

在给定侦察区域的前提下，无人机以视频侦察的任务模式，完成区域的全覆盖侦察。但在执行任务前，需预先规划相应的侦察航迹，使得无人机能沿着设定航迹自主完成侦察任务。

针对无人机视频侦察任务模式，首先考虑视频载荷的运动特点，根据其运动特性分析成像规律，确定周期性成像范围，可为后续制定覆盖策略提供依据。然后结合扫描线法确定航带数量，最后用每条航带的实际成像范围对任务区域进行分割，降低算法的未覆盖率，以保证所有航带的侦察范围能覆盖任务区域。

航迹规划具体步骤如下所示：

步骤1输入算法参数。输入飞机平台参数、载荷 参数及任务参数，作为后续计算的输入。

步骤2视频摆扫成像。利用视频摆扫成像法得到 周期成像范围内接矩形的长、宽等参数。

步骤3侦察区域分割。依据Case 1～3 三种情况， 判断航带实际成像范围长度与航带路径代价的关系。然后用每条航带的实际成像范围分割侦察区域。

步骤4最优侦察航向。结合算法指标约束，给出 区域覆盖的最优侦察航向，保证未覆盖率及路径代价等指标最优或次优。

步骤5输出侦察航迹。求解得到航向及航带参数 后，可输出一系列的航程点作为视频侦察的任务航迹。

4 实 验

4.1 实验平台

1）工作站型号：Thinkstation D30；CPU：Intel Xeon E5-2620（双处理器），64G 内存，64 位Win7 系统；编程工具：Matlab 2017b（64 位）。

2）侦察载荷综合测试及仿真平台（实验室自研）。

平台界面如图6所示。

图6 侦察载荷综合测试及仿真平台 Fig.6 Comprehensive test and simulation platform for reconnaissance load

4.2 实验内容及相关参数设置

在目标区域内规划视频覆盖侦察航迹，实现对区域的全覆盖侦察，同时满足未覆盖率及路径代价等指标要求。待侦察覆盖多边形区域如图7所示。

算法仿真参数如表1所示。

图7 待侦察覆盖区域 Fig.7 Reconnaissance coverage area

表1 仿真参数设置 Tab.1 Simulation parameter settings

4.3 评价准则

为评估算法的运行效率，以未覆盖率、路径代价和多余覆盖率作为侦察航迹的评价指标。

指标1：未覆盖率。未覆盖率是指任务区域中未覆盖区域的面积和占整个任务区域面积的百分比。定义式如下：

其中，Se为未覆盖区域的面积和，S为任务区域面积。

指标2：路径代价。路径代价是指由算法规划得到航迹的路程大小。定义式如下：

其中，L1为航带部分的路径代价和，L2为航带间边界部分的路径代价和。

指标3：多余覆盖率。多余覆盖率是指在任务区域外成像范围面积占任务区域面积的百分比。定义式如下：

其中，Sa为成像范围总面积。

4.4 仿真结果分析

实验一：摆扫成像规律实验

利用表1参数及实验平台，对一个周期视频摆扫的成像面积进行了实验，结果如图8所示。

将实验结果分析如下：

1）图8(a)是在侦察载荷综合测试及仿真平台上得到的实验结果，能够得到所有视频帧的点坐标及最终不规则多边形区域的点集和面积。

2）图8(b)红色部分是一个周期内所有视频帧的集合，蓝色是视频帧围成不规则多边形的边界范围。由此可知，一个周期的视频摆扫范围内不存在不连通区域，即无覆盖盲区，且相邻视频帧之间重叠率很高。

3）图8(c)红色部分是在不规则成像范围取的内接矩形。显然，内接矩形的长与左右摆扫的最大角度有关。

4）只要一个周期成像范围不存在盲区，那么整数周期的成像范围也是不存在盲区的。同样，相邻周期的成像范围间重叠率也很高。

5）内接矩形的长、宽参数，如表2所示。可用于下一步计算相关航带参数。

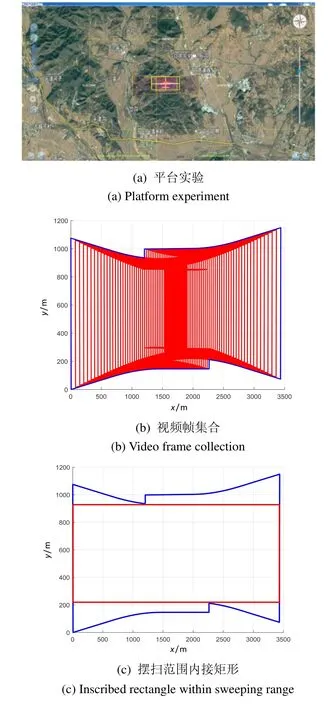
图8 视频摆扫实验 Fig.8 Video sweep experiment

表2 内接矩形参数 Tab.2 Inscribed rectangle parameter

实验二：视频侦察航迹规划实验将航向角σ从0 开始，每隔1°取值并进行实验。同时记录每次实验对应的算法指标数据，实验结果如图9所示。

将实验结果分析如下：

1）定义航向角σ为飞行方向与y轴的夹角，取值范围为0 ≤σ≤ π（在π ＜σ≤ 2π时航迹方向，与σ- π时的航迹方向相反）。

2）图9(a)～(d)中，红色实线表示侦察航迹；红色虚线框围成的矩形表示每条航带的实际成像范围。由 于视频摆扫成像的规律，导致航带的实际成像长度与航带的路径代价不一定是相等的。

图9 视频摆扫航迹规划实验 Fig.9 Video sweeping path planning experiment

3）用每条航带的实际成像范围分割侦察区域，会在航带两侧产生一定的未覆盖区域或多余覆盖区域。

4）将算法指标分别进行了归一化处理，如图10所示，横坐标表示航向角大小，纵坐标表示算法指标的归一化值。

综合考虑三个算法指标，认为σ=55°是最优侦察航向。此时规划得到的侦察航迹也是最优的，对应指标数据如表3所示。

表3 指标数据 Tab.3 Indicator data

图10 算法指标百分比 Fig.10 Algorithm indicator percentage

实验三：非摆扫成像实验无人机执行视频侦察任务时，视频载荷的工作模式有多种。非摆扫成像模式要求视频载荷静止不动（相对于无人机），且始终保持垂直对地成像。依据表1仿真参数（摆动范围、摆动速度设为0），结合非摆扫成像模式及扫描线法，可得到如图11 所示的视频侦察航迹（航向角σ=55°）。

图11 视频非摆扫航迹规划实验 Fig.11 Video non-sweeping path planning experiment

在非摆扫模式下，航带成像范围宽度d1由飞行高度和旁向视场角决定。航带间距d2由航带成像范围宽度和旁向重叠率决定。

注：由于航带间距比较小，航带数量较多。为了不影响仿真结果的可视性，没有将各航带的成像范围表示出来。

将实验结果对比分析如下：

1）在摆扫模式下的航带成像范围宽度为3.428 km（由表2可知）。在非摆扫模式下的航带成像范围宽度为0.750 km。即在相同航带条件下，摆扫模式下的成像范围更大，效率更高（摆扫范围角度越大，航带成像范围宽度也就越大）。

2）由于摆扫模式下航带成像范围宽度远大于非摆扫模式，因此摆扫模式下视频侦察航带间距远大于非摆扫模式下的视频侦察航带间距（同旁向重叠率），航带数量更少，路径代价更小。

3）在无人机航程、航时有限的条件下，算法路径代价大小限制了算法的可行性。摆扫模式下的视频侦察航迹路径代价要远小于非摆扫模式下的视频侦察航迹。所以摆扫模式下的视频侦察航迹更符合无人机性能限制，可行性更强。

实验四：视频侦察成像实验基于摆扫成像的无人机视觉侦察航迹规划方法，可在给定任务参数、飞机参数和载荷参数的前提下，依据任务要求为无人机规划出最优的侦察覆盖航迹，以降低未覆盖率。

为验证算法的有效性，结合实验室条件，设计了如下的飞行试验：采用某型六旋翼无人机及配套的双光载荷，对某任务区域进行视频侦察（该任务区域的地理高程数据已知），无人机的侦察航迹由本文算法规划得到，并通过无人机上行数据链将航程点数据装订至无人机飞控计算机。

通过对无人机采集到的视频数据进行拼接处理，得到侦察区域的态势图，以分析视频侦察是否存在盲区来验证算法的有效性。侦察区域拼接态势图如图12 所示。

图12 侦察区域拼接图 Fig.12 Reconnaissance area mosaic

将实验结果分析如下：

1）通过对视频数据进行拼接处理，得到整个区域的态势图，不存在侦察盲区，满足侦察要求。

2）算法规划得到的侦察航迹，有效降低了侦察未覆盖率，提高了侦察效率，验证了算法的可行性。

5 结 论

通过理论推导与实验验证，对算法的合理性与优越性进行了说明，主要得到以下结论：

1）针对视频载荷的摆扫运动规律，推导给出成像范围的计算方法，为制定视频覆盖策略提供了依据。

2）基于视觉成像的区域分割法是利用航带实际成像范围分割区域，降低了算法的未覆盖率。

3）以路径代价、未覆盖率和多余覆盖率为指标，给出最优侦察航向及航迹，使得无人机能以最经济、效率最高的航迹完成侦察任务。

4）局限性：对周期摆扫范围近似取内接矩形，会一定程度上提高算法的多余覆盖率。

5）推荐应用范围：适用于以视频侦察为任务背景的航迹规划。