以问题为导向的数学创新意识培养
白凌晓
《义务教育数学课程标准(2011年版)》新增了“创新意识”这一核心概念,并且指出“创新意识的培养是现代数学教育的基本任务,应体现在数学教与学的过程之中”,“创新意识的培养,应该从义务教育阶段做起,贯穿数学教育的始终”。那么,在日常的小学数学课堂上,如何培养学生的创新意识呢?
数学是具备高度创造性的学科,无论是命题的归纳、逻辑的演绎、公式的推导、习题的演算都充满着创新性。小学数学课堂教学应把树立“问题意识”作为培养学生创新意识的重要抓手。教师应引导学生通过数学知识的习得、数学命题的推证、数学素质的生活运用等途径发现新问题、求证新问题,为学生终身学习及未来职业生活打下坚实的基础。
一、观察试验,引发猜想
教师在数学教学中有意识设计供学生观察试验、猜想命题、寻找规律的练习,能发展学生的创造性思维。如:一年级下册《找规律》的“做一做”中给出的涂色、填数、摆放、填画等都是有一定规律的,教师可以引导学生从颜色、声音、数量、大小、形状、数字关系、方向及其他性质着手发现直观的规律,如果学生能进一步发现抽象而隐蔽的规律——图形的排列有什么规律,数字的排列就有相应的变化规律,则说明学生的创造性思维上升了一个高度,也就种下了创新意识的一颗种子。
二、数形结合,萌生构想
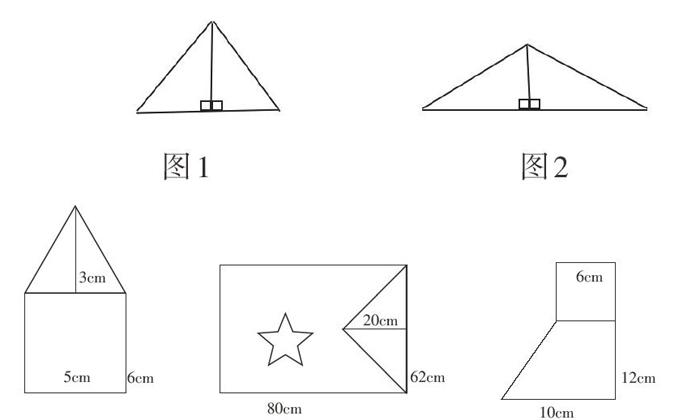
数学教学中,抓住数形结合,引导学生从几何角度去看代数问题,或者从代数角度看几何问题,是培养创造性想象力的有效途径。教学四年级下册的《三角形的内角和》时,首先以“数”构“形”:学生通过测量,得出三角形的内角和可能是180°。究竟是不是180°呢?教师引导学生通过剪(撕)、拼,将三角形的三个内角转化成平角,运用几何直观,揭示问题本质。第二,以“形”思“数”:学生通过剪长方形、正方形,由已知长方形、正方形的内角和计算出三角形的内角和是180°。第三,数形相依,各展其长。用两个完全一样的直角三角形拼成一个大的锐角三角形(图1),这个大的锐角三角形的内角和是180°×2-180°=180°,同理推出钝角三角形(图2)的内角和同样是180°。
三、发散求异,多方设想
发散思维能力有助于学生提出新问题,孕育新思想,建立新概念,构筑新方法。在数学教学中,一题多解是培养学生发散思维、发展学生数学创造性思维的一条有效途径。如:五年级上册《多边形面积的整理和复习》,在“课前小研究”教学活动中,教师设计“我会编”环节,让学生自编一道关于组合图形面积的问题并解答。学生设计出了如下图所示的三幅组合图形。
学生在解决平面组合图形面积中,无论是运用分割、平移,还是采取转化、补全等各种方法,实则离不开“等积变形”的数学思想,而通过自主设计和计算求解,学生的思维由发散到聚合,由直观到深刻。
四、直觉顿悟,突发奇想
数学直觉是对数学对象的某种直接领悟或洞察。在小学数学教学中可以从估一估、猜一猜、整体把握等方面去创设情境,诱发直觉。如:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡、兔各几只?”这样的问题。《孙子算经》中是这样解答的,假如砍去每只鸡、每只兔一半的脚,则每只鸡就变成了独角鸡,每只兔就变成了双腿兔。这样鸡和兔的脚的总数就由94只变成了47只。如果笼子里有一只兔子,则脚的總数就比头的总数多1,因此,脚的总只数47与总头数35的差,就是兔子的只数。这一思路新颖而奇特,一般小学生并不一定能够想得到,需要教师在教学时做有效的引导。
五、群体智力,民主畅想
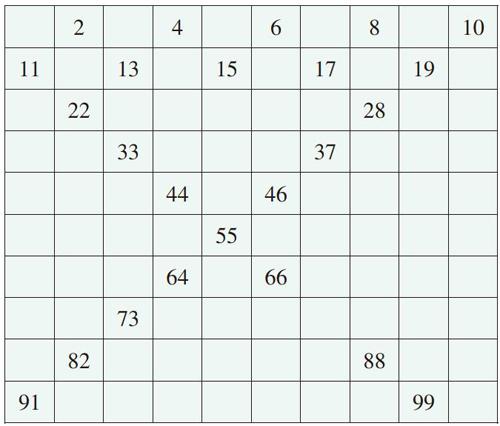
良好的教学环境和学习气氛有利于培养学生的创造性思维能力。课堂上,教师对学生讲授解题技巧是纵向交流、垂直启发,而学生之间的相互交流和切磋则可以促进个体之间创造性思维成果的横向扩散或水平流动。如一年级下册“百数表”的教学,教师让学生通过填“百数表”中的数,找出数的排列规律(如右图)。
通过讨论交流,学生构建起数与数之间的逻辑关系,清楚地掌握了100以内数的排列顺序,探究出百数表中隐含的诸多规律。如:第一横行的5个数都是双数,第二横行的5个数都是单数;从左上到右下这一斜行中的数(11、22、33、44……)个位、十位数字都相同;从右上到左下一行数中(10除外),十位上的数从1开始,逐渐多1直到9,而个位上的数则相反,从9开始逐渐少1直到1,等等。
以上几点可操作性的方法,教师在采用时应因时、因地、因内容、因对象而异。只有综合得当地融入自己的教学设计,才能收到预期的效果。
(作者单位:襄阳市教育科学研究室)

