Connectivity and the Super Connectivity of Exchanged Folded Crossed Cubes

CAI Xuepeng, YANG Wei, DU Jie, REN Baitong

(College of Mathematics and Physics, Xinjiang Agricultural University, Urumqi 830052, China)

Abstract：The crossed cube CQn and the exchanged crossed cube ECQ(s, t) are two common topology in the computer system. ECQ(s, t) is obtained by systematically removing links from a binary crossed cube CQn. A new interconnection network, named exchanged folded crossed cube EFCQ(s, t), is obtained, which is basically a standard exchanged crossed cube ECQ(s, t) with some extra edges constructed between the nodes. The connectivity and the super connectivity are the two significant factors for measuring the reliability and fault tolerance of the interconnection network. In this work we show that the connectivity of EFCQ(s, t) is equal to its minimum degree, and the super connectivity of EFCQ(s, t) is equal to its minimum edge-degree.

Key words：crossed cube; exchanged crossed cube; exchanged folded crossed cube; connectivity; super connectivity

1 Introduction

We consider only finite, undirected, simple and connected graphs. For the graph definitions and notation we follow ref. [1].

LetG=(V,E) be a graph. For subgraphsHandKofG, letG-Hdenote the subgraph which is induced byV(G)-V(H), and letNH(K) denote the set of vertices inHthat are adjacent to some vertex inK. In particular, ifKconsists of one vertexv, we omit the brackets, and letdG(v)=|NG(v)| be the degree ofvinGandNG[v]=NG(v)∪{v}. If no ambiguity can arise, we omit the indices and just writed(v),N(v) andN[v] etc.δ(G) is the minimum degree ofG. The minimum edge-degree of a graphGis defined asξ(G)=min{d(u)+d(v)-2|(u,v)∈E(G)}.

A vertex cutS(resp. edge cut) ofGis a vertex (resp. edge) set ofGsuch thatG-Sis disconnected or trivial. As an important measure of the vulnerability and fault-tolerance of the network, the connectivity (resp. edge-connectivity) ofG, denoted byκ(G) (resp.λ(G)), is defined as the minimum size over all the vertex cuts (resp. edge cuts) ofG. As more refined indices, Esfahanian and Hakimi in ref. [2] introduced restricted connectivity (resp. restricted edge-connectivity) by considering vertex cuts (resp. edge cuts) that satisfy some conditions. Based on this concept, the super connectivity and the super edge-connectivity were proposed in ref. [3].

A setS⊆V(G) (resp.S⊆E(G)) is called a super vertex cut (resp. super edge cut) ofGifG-Sis disconnected and every remaining component has at least two vertices. Note that the super vertex cuts or super edge cuts do not always exist. The super connectivity (resp. super edge-connectivity) ofG, denoted byκ(1)(G) (resp.λ(1)(G)), is the minimum cardinality over all super vertex cuts (resp. super edge cuts) if there is any, and is +∞ otherwise by convention. During the last two decades, among a large number of results on a various kind of restricted connectivity measures of networks (graphs), many research works on the super connectivity and the super edge-connectivity of networks have been reported. We refer to [4-19] for more details.

The underlying topology of an interconnection network is usually presented by a connected graph, where the vertices represent the processors and the edges represent the communication links in the network[20]. There are many useful, vital and interesting topologies proposed in interconnection networks, in which hypercubeQn[21]is the most popular and efficient interconnection networks due to their rich topological properties, such as small diameter, symmetry, recursive structure and so on. Many variants of hypercube were proposed to overcome some disadvantages ofQn. For example, crossed cubeCQn[22-23], folded hypercubeFQn[24], exchanged hypercubeEH(s,t)[25], exchanged folded hypercubeEFH(s,t)[26]and so on. Then-dimensional crossed cubeCQn,n-dimensional folded crossed cubeFCQn[27-28]and exchanged crossed cubeECQ(s,t)[29]are regarded as three of the most important interconnection networks for parallel computer systems. Based on these three interconnection networks, a new interconnection network called exchanged folded crossed cube, denoted byEFCQ(s,t), was introduced by Bhavani et al in 2018[30]. Many properties of exchanged folded crossed cube have been studied. The diameter ofEFCQ(s,t) is less than that ofQn,EH(s,t),CQn, andECQ(s,t). The factors like cost, diameter, degree, edges, and isomorphism which effect the performance of the system for different interconnection networks are compared. For the details of the researches onEFCQ(s,t) see ref. [30].

In this paper, we will determine that

κ(EFCQ(s,t))=λ(EFCQ(s,t))=s+2,

κ(1)(EFCQ(s,t))=λ(1)(EFCQ(s,t))=2s+2s≤t.

The rest of this paper is organized as follows: In Section 2, we present some related definitions, properties, lemmas and notations used in the paper. In Section 3, we determine the connectivity ofEFCQ(s,t), and the super connectivity ofEFCQ(s,t). Finally, some concluding remarks is given in Section 4.

2 Definitions and Lemmas

Definition1Two binary stringsx=x1x0andy=y1y0are pair related, denoted byx～y, if and only if (x,y)∈{(00, 00), (10, 10), (01, 11), (11, 01)}.

Letx=xn-1xn-2…x0be a binary string of lengthn. We setx[i]=xiandx[j:i]=xjxj-1…xi, where 0≤i≤j≤n-1.

Definition2[29]The exchanged crossed cube is defined as an undirected graphECQ(s,t)=G(V,E), wheres≥1 andt≥1 are positive integer. The vertex set of a exchanged crossed cubeECQ(s,t) isV={(as-1…a0bt-1…b0c|ai,bi,c∈{0, 1}, 0≤i≤s-1, 0≤j≤t-1}. The set of edgesisE={(u1,u2)|(u1,u2)∈V×V} is composed of three disjoint typesE1,E2andE3. The two verticesu1andu2inECQ(s,t) are connected inECQ(s,t) if it satisfies the following conditions:

E1:u1[s+t:1]=u2[s+t:1],u1[0]≠u2[0];

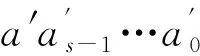
By definition, it is immediate to get that there are 2s+t+1vertices inECQ(s,t) and the number of edges inECQ(s,t) is (s+t+2)2s+t+1.

In ref. [29-30], authors showed some properties ofECQ(s,t).

Theorem1[29]ECQ(s,t) is isomorphic toECQ(t,s).

Theorem2[29]ECQ(s,t) can be decomposed into two copies ofECQ(s-1,t) orECQ(s,t-1).

Theorem3[29]ECQ(s,t) can be divided into 2tdisjoint subgraphs isomorphic toCQsand 2sdisjoint subgraphs isomorphic toCQt.

Fig. 1 ECQ(1, 2) and EFCQ(1, 2)

Theorem4[31]κ(ECQ(s,t))=λ(ECQ(s,t))=s+1, where 1≤s≤t.

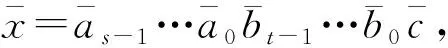
Fig. 1 showsECQ(1, 2) andEFCQ(1, 2).

Notation1EFCQ(s,t) can be decomposed into two subgraphsLandR, where

V(L)={0as-2…a0bt-1…b0c|ai,bj,c∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1},

V(R)={1as-2…a0bt-1…b0c|ai,bj,c∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1}.

LandRare the subgraphs induced byV(L) andV(R) respectively. ObviouslyLandRare both isomorphic toECQ(s-1,t) and the edges betweenLandRconsist ofE1and complementary edgesE4ofEFCQ(s,t). We writeEFCQ(s,t)=L⊗R. Then we can further divideV(L) into two vertex subsets,AandB, andV(R) into two vertex subsets,CandD, where

A={0as-2…a0bt-1…b01|ai,bj∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1},

B={0as-2…a0bt-1…b00|ai,bj∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1},

C={1as-2…a0bt-1…b00|ai,bj∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1},

D={1as-2…a0bt-1…b01|ai,bj∈{0, 1}, 0≤i≤s-2, 0≤j≤t-1}.

We haveA∪B=V(L) andC∪D=V(R). The edges betweenAandB(orCandD) lie inE1and consist of a perfect matching of the subgraph induced byA∪B(orC∪D). The edges betweenBandClie inE2and consist of a perfect matching of the subgraph induced byB∪C. The edges betweenAandC(orBandD) lie inE4and consist of a perfect matching of the subgraph induced byA∪C(orB∪D).

Theorem5[30]The vertices which have the bit address ending with 0 inEFCQ(s,t) have the degrees+2. The vertices which have the bit address ending with 1 inEFCQ(s,t) have the degreet+2.

Theorem6[30]EFCQ(s,t) is isomorphic toEFCQ(t,s).

By the above Theorem 1 and Theorem 6, we can always assumes≤tin the following discussion. Thenδ(ECQ(s,t))=s+1 andδ(EFCQ(s,t))=s+2.

From the above Definition 3 and Theorem 3, it is immediate to get the following observation.

Observation1EFCQ(s,t) can be divided into 2tdisjoint subgraphs isomorphic toCQsand 2sdisjoint subgraphs isomorphic toCQt. Set l={Li|Li≅CQs, 1≤i≤2t} and R={Rj|Rj≅CQt, 1≤j≤2s}.

(1)There are no edges between any two subgraphsLiandLmfori≠m. Similar forRjandRn.

(2)Each vertexuinLiis adjacent to two vertices which lie in differentRj. Each vertexvinRjis adjacent to two vertices which lie in differentLi. Furthermore, for different vertices in eachLi, their neighbors lies in differentRj.

In ref. [4, 23], authors prove thatCQncontains no 3-cycle forn≥3, and any two nonadjacent vertices inCQnhave common neighbors at most two forn≥4. Hence, it is easy to get the following Lemma.

Lemma1EFCQ(s,t) contains no 3-cycle and any two nonadjacent vertices inEFCQ(s,t) have common neighbors at most two.

3 Connectivity and Super Connectivity of Exchanged Folded Crossed Cubes

Lemma2κ(EFCQ(1,t))≥3, wheret≥1.

ProofLetFbe an arbitrary set of vertices inEFCQ(1,t) such that |F| ≤2. We are going to prove thatEFCQ(1,t)-Fis connected.

Ift=1, then the result is valid by the definition ofEFCQ(1, 1).

Lett≥2,EFCQ(1,t) can be partitioned into subgraphsL1andR1, where

V(L1)={a0bt-2…b0c|a,bj,c∈{0, 1}, 0≤j≤t-2},

V(R1)={a1bt-2…b0c|a,bj,c∈{0, 1}, 0≤j≤t-2}.

L1andR1are the subgraphs induced byV(L1) andV(R1) respectively. ObviouslyL1andR1are both isomorphic toECQ(1,t-1) and the edges betweenL1andR1consist ofE1and complementary edgesE4ofEFCQ(1,t).

For convenience, letFL1=F∩L1andFR1=F∩R1. Without loss of generality, we may suppose that |FL1| ≥|FR1|. Then |FR1| ≤1.

SinceR1≅ECQ(1,t-1), by Theorem 4, we haveR1-FR1is connected. Next, we will show that any vertexuinL-FL1is connected via a path to a vertex inR1-FR1. We distinguish the following cases.

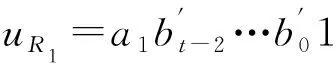
Theorem7κ(EFCQ(s,t))=λ(EFCQ(s,t))=s+2, where 1≤s≤t.

ProofSinceδ(EFCQ(s,t))=s+2,κ(EFCQ(s,t))≤s+2. Next, we will prove thatκ(EFCQ(s,t))≥s+2.

Ifs=1, thenδ(EFCQ(s,t))=s+2=3. Then we can get thatκ(EFCQ(s,t))=s+2=3 by the Lemma 2. By Notation 1,EFCQ(s,t)=L⊗R.

Lets≥2. By Theorem 4, we can knowκ(L)=κ(R)=s. LetSbe a minimum vertex cut ofEFCQ(s,t).

The following cases are considered.

Case1L-SandR-Sare both connected.

ThenSmust contain at least an endpoint for each edge inE4. This yields |S|≥|E4|≥2s+t>2s+1>s+2 fort≥s≥2, a contradiction.

Case2L-SorR-Sis not connected.

Fig. 2 Illustration of the Proof of Case 2 of Theorem 7

Without loss of generality, suppose thatL-Sis not connected. By Theorem 4,Shas leastsverticesinL. For convenience, letSL=S∩LandSR=S∩R.

Suppose that |SR|≥2, then |S|≥s+2.

WithSbeing a minimum vertex cut and |S|≥s+2, we get thatκ(EFCQ(s,t))≥s+2. Thenκ(EFCQ(s,t))=s+2. Byκ(EFCQ(s,t))≤λ(EFCQ(s,t))≤δ(EFCQ(s,t)), we complete the proof of Theorem 7.

Theorem8κ(1)(EFCQ(s,t))=2s+2.

ProofWe firstly proveκ(1)≤2s+2 wheres≤t. Take (u,v)∈E2inEFCQ(s,t) and letX={u,v},S=NEFCQ(s, t)-X(X). By Observation 1, we know that the graph induced byuandvis a subgraph ofCQs. SinceEFCQ(s,t) has no 3-cycle, it is easy to know |S|=2s+2. Since |X∪S|=2s+4<2s+t+1,Sis a vertex cut ofEFCQ(s,t). Now we show thatSis a super vertex cut ofEFCQ(s,t). LetY=EFCQ(s,t)-Sandwbe a vertex inY. We will show thatwhas at least one neighbor inY. By Lemma 1, we may get thatwhas at most two neighbors inS. Thus,whas at leasts+2-2 (≥1) neighbor(s) inY. Hence S is a super vertex cut ofEFCQ(s,t) andκ(1)(EFCQ(s,t))≤2s+2.

Now, we will prove thatκ(1)(EFCQ(s,t))≥2s+2. LetKbe any vertex subset ofEFCQ(s,t) with |K|≤2s+1 such thatEFCQ(s,t)-Khas no isolated vertices. Next, we will show thatEFCQ(s,t)-Kis connected. By Notation 1,EFCQ(s,t)=L⊗R. For convenience, letKL=K∩LandKR=K∩R. Without loss of generality, we may suppose that |KL|≥|KR|. Then |KR|≤s. We consider two cases.

Case1R-KRis connected.

We are going to prove that any vertexuinL-KLis connected toR-KR. We distinguish the following subcases.

Subcase1u=0as-2…a0bt-1…b00∈B.

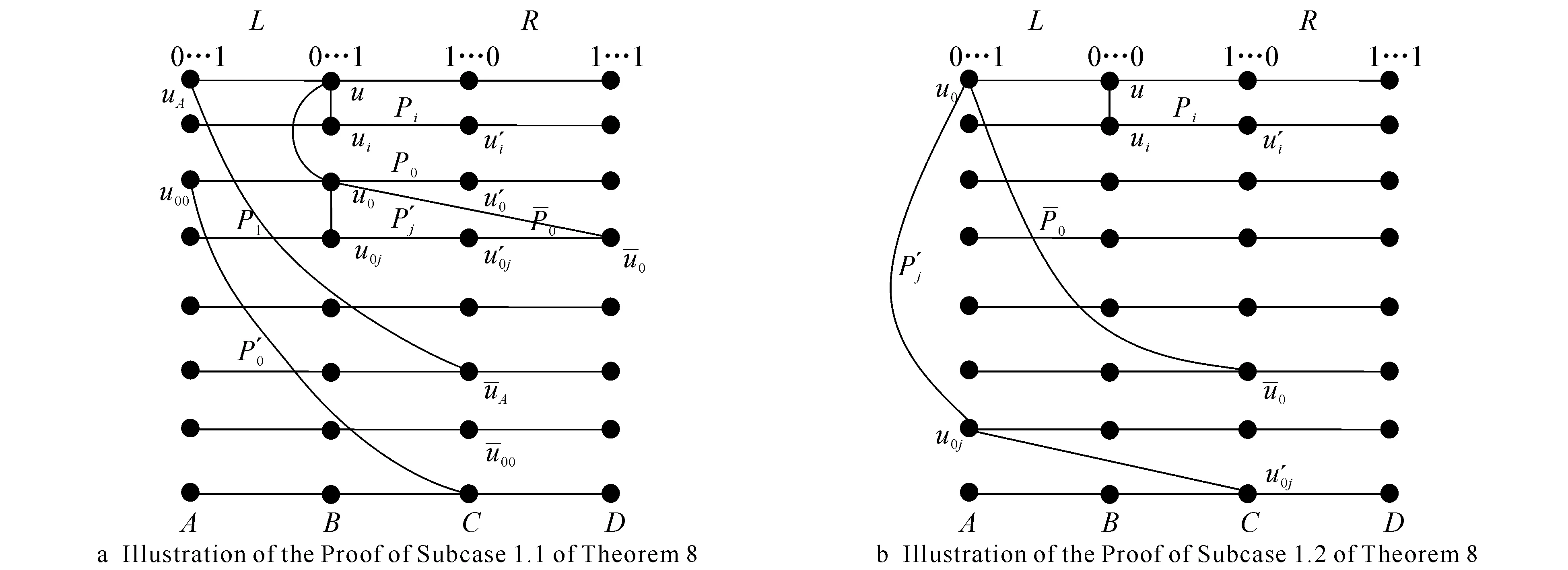
Fig. 3 Illustration of the Proof of Subcase 1 of Theorem 8

Subcase1.1u0∈B.

Claim1These 2spaths connectinguoru0to a vertex inRare disjoint except foruandu0.

Subcase1.2u0∈A.

Obviously, it is immediate to get the following Claim 2.

Claim2Theses+tpaths connectinguoru0to a vertex inRare disjoint except foruandu0.

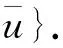
Subcase2u=0as-2…a0bt-1…b01∈A.

Fig. 4 Illustration of the Proof of Subcase 2 of Theorem 8

Subcase2.1u0∈A.

Claim3These 2t+1 paths connectinguoru0to a vertex inRare disjoint except foruandu0.

Subcase2.2u0∈B.

Claim4Theses+t+1 paths connectinguoru0to a vertex inRare disjoint except foruandu0.

Claim 3 and Claim 4 imply in Subcase 2. 1 we can get at least 2s+1 vertex disjoint paths except foruandu0connectinguoru0to a vertex inR. Since |K|≤2s+1, removingKbreaks at most 2sthese paths. It states that there is a path connecting anyuofL-KLto a vertex ofR-KR. HenceEFCQ(s,t)-Kis connected. Thenκ(1)(EFCQ(s,t))≥2s+2. Soκ(1)(EFCQ(s,t))=2s+2.

Case2R-KRis disconnected.

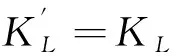
From the definition ofEFCQ(s,t), we haveξ(EFCQ(s,t))=2s+2 for 1≤s≤t. In ref. [2], it is shown thatλ(1)(G)≤ξ(G) in any graphGwhich is not a star graph and has at least four vertices. Therefore,λ(1)(EFCQ(s,t))≤2s+2. By following the proof of Theorem 8 withKbeing an edge set, we can get thatλ(1)(EFCQ(s,t))≥2s+2. Then we have the following theorem.

Theorem9λ(1)(EFCQ(s,t))=2s+2.

4 Concluding Remarks

In this paper, we show that the connectivity ofEFCQ(s,t) are equal to its minimum degree and the super connectivity ofEFCQ(s,t) are equal to its minimum edge-degree.

For an integerh≥0, theh-restricted (edge-) connectivity of a connected graphG, denoted byκ(h)(G)(λ(h)(G)), is the minimum cardinality of a set of vertices (edges), if any, whose deletion disconnectsGand every vertex of the remaining graph has degree at leasth. Note thatκ(0)(G)=κ(G),λ(0)(G)=λ(G) andκ(1)(G)(λ(1)(G)) is the super (edge-) connectivity ofG[27, 31]. It would be of interest to consider theh-restricted (edge-) connectivity of the exchanged folded crossed cubes forh≥2.