整合教材典型问题 发展学生数学学力*——高一“函数”单元复习课的实践与思考

罗建宇

一、问题背景

笔者曾在教研室工作了几年，调研中发现，不少高中数学老师不重视设计起始年级的单元复习课。老师的普遍做法是知识罗列，或以习题课代替；稍微有点思考的老师，则将其设计成了专题复习课，拔高了要求，有了高三的味道，导致单元复习课缺乏针对性、有效性和系统性。更有甚者，在一个章节教学刚结束就立即开启了下一章节的新授课教学，直接忽视了单元复习课的存在，更不利于学生整体地认识章节知识。

笔者在一次教研活动中，在高一年级开设了一节《函数复习课》，表达了“整合教材典型问题，发展学生数学学力”的观点，获得一致好评。笔者想通过这一节课的教学展示，引导大家关注高一年级的单元复习课。那么，如何上好这一节高一的单元复习课呢？我思考了如下三个问题：（1）选题要典型；（2）复习内容要涵盖函数的主干知识和思想方法；（3）让学生“编制”一些问题，增强参与性并提高问题意识。针对上述问题及高一学生学习特点，笔者从课本一道经典习题的函数模型出发进行教学设计，逐步通过分析、变式、联想、引申等过程，对函数的主干知识和思想方法进行复习，且使得到的“新”函数模型仍是典型的函数模型，从而将教材典型问题进行串联整合，以期望引导师生关注课本典型习题，感悟习题蕴含的重要知识与方法。

为展现朴实却灵动的数学课堂，传递在课堂中不过分依赖“导学案”的思想，笔者采用了留白的方式（变式、引申、串讲等问题不印出来，根据教学实际情况在课堂上引出）设计了导学案（见图1），课前发放给学生预习。

二、教学设计与生成

1.预习设计。

例题与变式1、2 见图1。

图1

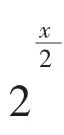
变式2 的题干部分没有写完，它是一个简单问题：解不等式f（1-m）+f（1-m2）＜0，利用例1 前两问的结论即可完成。这样设计主要考虑以下两个原因。

（1）选择这个问题，是为了完整复习单调性定义中包含的三个方面。我们知道，单调性（以单调递增为例）定义：如果对于区间I 内的任意两个值x1x2，当时x1＜x2，都有f（x1）＜f（x2），那么就说y=f（x）在区间I 上是单调递增的。数学概念定义的条件和结论都是互为充要条件的，因此其逆命题亦成立。视“x1＜x2”为条件①，“f（x1）＜f（x2）”为条件②，“y=f（x）在区间I 上是单调递增”为条件③，在解题教学中常有三个情形：①②→③用作定义法证单调性（例1 第2 小问）；①③→②用作比大小、求值域（变式1 第2小问）；②③→①用作利用单调性解不等式（常与奇偶性结合），其中条件①中两值需在给定的（单调）区间内（即变式2）。

（2）这个问题在课堂上解答并不难，选择在学案上留白，于课堂中生成，更能彰显课堂的灵动，同时通过变式让学生巩固和回忆以前学习的知识（题型），为下一步的“联想”做铺垫。

2.联想设计。

请回忆先前学习的知识和解答过的问题，基于上例函数提出一个数学问题并解答。

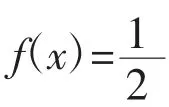
【设计意图】让学生分组解决问题并阐述解决方法，复习相关知识点，使概念、思想、方法成系统。通过这一教学环节的设计，不仅让学生回忆了已学知识，而且知晓这些知识之间的联系和区别，经历提出问题、分析问题、解决问题过程，有效培育学生“四基四能”，提升学生数学核心素养。

3.探究设计。

变式3 见图1。

【设计意图】变式3 实则为探究设计，它的解决，大部分学生是依据奇函数定义，通过运算得到k=±1，用此类问题训练运算能力也是设置本题的目的之一。选用本题还有两个想法，一是解决此类填空题时，可以奇函数的定义域特点作考虑，若其为R，由f（0）=0，得k=1，若其不为R，由定义域（即x≠log2（-k））关于原点对称，可得k=-1；二是当k=1 时，函数为例题所选函数（已研究），当k=-1 时的函数如何研究，为下一步“串讲”做铺垫。

4.串讲设计。

串讲2：示例中的解析式，能否用函数表示。

【设计意图】串讲1 中的函数仍然是典型的函数模型，要作其草图，需要像探索例题的每个小问一样，先研究函数性质，通过性质整体把握函数特征，再作出函数的图象（草图），进而巩固这一研究函数图象性质的一般方法。将串讲1的函数图象与例题中的函数图象画在同一个坐标系中（可用数学软件演示），可以发现，例题中函数零点的位置对应串讲1 中函数图象的渐近线，揭示了互为倒数关系的函数的图象关系。

三、几点思考

《普通高中数学课程标准（2017 年版）》明确提出我国高中学生的数学核心素养为：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析。华东师范大学徐斌艳教授在概述国内外数学学力研究的基础上，提出了我国数学学力模型的构建思路，即在具有国际视野、体现我国特色的前提下，将数学教学看作数学活动的教学，以数学活动为视角，提出包括数学地提出问题、数学表征与变换、数学推理论证、数学建模、数学地问题解决和数学交流等六大数学学科核心能力。［1］数学核心素养与数学学力并不是相互独立的。数学核心素养对整个数学教学具有指导意义，起着统领性的作用。数学学力则可视为在核心素养指导下的具体的操作方法，是具化数学核心素养的现实路径。笔者在本节课的教材典型问题的整合中，充分考虑了学生数学核心素养的形成和数学学力的发展。笔者以为，单元复习课是发展学生数学学力的重要课型。为了更好地促进单元复习课的实施，也为了更好发展学生的数学学力、提升学生的数学核心素养，在进行单元复习课时，需要考虑以下几点——

1.例题选取突出典型示范。

当前的高一复习课中，照搬高三复习资料中的成品例题现象严重，导致教学起点过高、难度过大，进而造成教学重心偏移，起不到基础年级应有的复习效果。因此，高一单元复习课教学的例题选择一定要注意针对性、适度性和思考性。［2］实际上，教材中有很多适合学生认知特点的典型例题，对其进行恰当的变式、串讲、改编后进行复习教学，能将单元知识内容有机融合，问题解决的方法得以提炼升华，在教学中起到很好的示范作用，对学生的思维训练与能力提升是有益的。本节课选择的例题即来源于教材，突出典型示范性，通过系列的变式、改编、联想、串讲，将“函数”一章的知识和方法进行系统的复习和梳理，有利于增强学生的课堂参与性，有效的提升学生的问题意识，发展学生“数学地提出问题”与“数学推理论证”两大数学学力。

2.教学设计注重单元整体。

由于学生在新课学习中获得的知识相对比较零散，因此比较容易遗忘或混淆，开设单元复习课就显得很有必要，这能从统整的角度对本单元的知识进行梳理、归纳、巩固，以达到厘清知识间逻辑关联，构建出整章知识网络，从而使学生对单元知识有整体把握，这既是概念教学的一种重构，也是一种单元整体观下的教学实践。

单元复习课教学还应通过示范让学生学会整理，对单元的知识能够进行有序合理地建构，通过图、表的方式，形成一个主线突出、脉络清晰、体系完整的知识结构。［3］本节课，通过对例题的解析、变式、联想、串讲，梳理了函数问题的一般研究路径：定义域→基本性质（单调性、奇偶性）→值域→应用（零点问题、恒成立问题、有解问题等）。在此基础上，辩证看待函数图象性质的研究方法，新授课教学中采用的是从形到数，即通过对基本初等函数（指数、对数、幂函数）的图象来归纳得到相应函数性质的；对新函数的研究则采用从数到形，即通过对函数的性质研究来作函数图象（草图）。这种思想方法通过单元复习课凸显和建构出来，形成今后进一步学习的经验和认知方式，正是单元复习课的价值所在。因此，单元复习课应该是研究内容与研究方法的融合，更重要的是，通过单元复习课能使学生获得研究一类问题的基本方法，并能在数学研究过程中，利用掌握的基本方法去尝试解决其他一些问题，将不熟悉的情境问题转化为已知的情境的问题并加以解决，有效地发展学生“数学地解决问题”与“数学表征与变换”两大数学学力。

3.教学过程关注学生交流。

当前的很多公开课、展示课活动中，因为授课老师课前精心做了过于“充分”的准备，常出现学生课前预习过于充分，上课的内容基本提前已知，导学案中呈现内容过多，课堂上学生对习题的变式引申的体会不深刻，思维锻炼深度不够的现象。［4］这样的课堂虽然看似热闹，学生参与度高，却思维训练不到位，华而不实，不能让学生经历真正的数学活动并积累基本活动经验。数学活动经验，是动作与心智交互作用的结果，要引导学生亲身经历，要“带着问题”亲身投入到数学活动中来，进行积极地观察、操作、实验、猜测、归纳、推理等活动，形成丰富的数学活动经验。因此，在数学课堂教学中，要注重学生的主动参与、成果交流，强调数学活动经验在学生的经历、自主探究和交流共享中的自然生长。教师不能急于数学知识的生成，不要让学生的经历、自主和交流演变成假性参与和假性交流，要把时间和机会留给学生，把课堂还给学生，把自己的精力放在鼓励学生自主探索和合作交流上，如此才能有效地发展学生“数学交流”这一数学学力。

当然，我们还应认识到数学学力的发展不可能仅通过一节课、一种课型就能发展起来，学生数学学力的发展是一个长期的过程。本文仅以整合教材典型问题作为切入点，探讨在单元复习课中如何有效地发展学生的数学学力，其他课型如何发展学生的数学学力，发展学生数学学力还有其他方式、方法吗等问题。教学研究永无止境。