对一道绳牵连体圆周运动例题的变式分析

湖南

(作者单位：湖南省长沙市长郡滨江中学)

圆周运动连接体，重点找准向心力。临界条件需注意，整体隔离破难题

圆周运动是高中物理曲线运动中的一个重要内容。通常以绳牵连体的形式出现，重点考查连接体的受力分析、圆周运动的规律及临界条件的判断，具有综合性较强的特点，是高中物理的一个重难点内容。以下通过对一道绳牵连体圆周运动例题进行分析与变式，来增强对该连接体模型的认识及其物理规律的理解与应用。

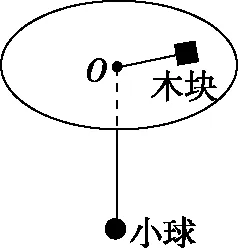
图1

【例题】如图1所示，在光滑水平转台上放一个质量M=2.0 kg的木块，绳的一端系住木块，另一端穿过转台的中心孔O(光滑)悬吊一质量m=1.0 kg的小球，当木块以v=1.0 m/s的初速度相对O孔恰好做匀速圆周运动时，已知重力加速度g=10 m/s2，木块、小球均视为质点，则木块到O孔的距离为

( )

A.10 cm B.15 cm C.20 cm D.25 cm

【答案】C

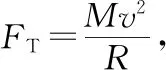
【点评】本例中水平转台表面光滑，木块不受摩擦力，绳子对木块的拉力提供木块做匀速圆周运动的向心力，结合圆周运动规律，再选小球作研究对象得到绳子拉力的大小，联立方程即可求解。

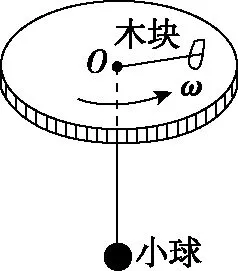
图2

【变式1】如图2所示，粗糙水平转台放一个质量M=2.0 kg的木块，木块与台面间的最大静摩擦力fm=6.0 N，绳的一端系住木块，另一端穿过转台的中心孔O(光滑)悬吊一质量m=1.0 kg的小球，当转台以ω=5.0 rad/s的角速度匀速转动时，欲使木块相对转台静止，已知重力加速度g=10 m/s2，木块、小球均视为质点，则木块到O孔的距离可能是

( )

A.16 cm B.5 cm C.60 cm D.30 cm

【答案】AD

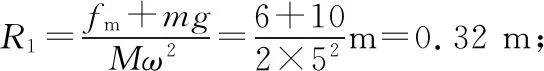
【点评】变式1与例1相比，难度明显增加。由于转台粗糙，对木块受力分析时需要考虑转台对木块的静摩擦力作用。同时需要注意，该静摩擦力的大小和方向会随着木块做圆周运动角速度的变化而变化。本题的关键是临界条件的选取。由题知木块受到的绳子拉力与木块所受转台静摩擦力的合力提供木块做圆周运动的向心力。当静摩擦力达到最大值并且方向与绳子拉力方向相同时，木块受到的向心力最大；此时对应木块做圆周运动的轨道半径达到最大；反之，当静摩擦力达到最大值并且方向与绳子拉力方向相反时，木块受到的向心力最小，此时对应木块做圆周运动轨道半径达到最小。本变式重点考查隔离法的应用及临界条件的判断。结合连接体的受力分析、准确找到木块所受向心力的极值，再给合圆周运动的规律便可求解。

【变式2】如图3所示，两个可视为质点、完全相同的木块A和B放在转盘上，两者用长为L的细绳连接，木块与转盘间的最大静摩擦力均为自身重力的K倍，A放在距离转轴为L的位置处，整个装置绕转盘中心的转轴O1O2转动。开始时，绳恰好伸直但无弹力，现让该装置从静止开始转动，使角速度ω缓慢增大，则以下说法正确的是

( )

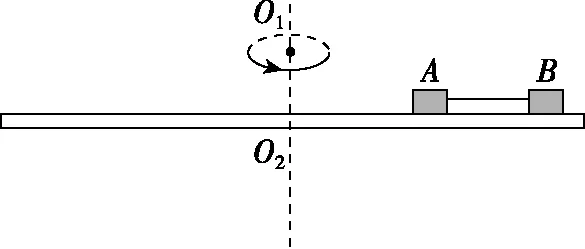
图3

【答案】ACD

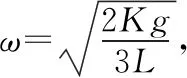
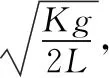
【变式3】如图4所示，可围绕竖直轴转动的水平圆盘上，放着用细绳相连的质量均为m的两个物体A和B，与圆心距离分别为RA=r，RB=2r，A、B与圆盘间的最大摩擦力均为重力的μ倍，在圆盘转动的角速度ω缓慢增大到物体刚好要发生滑动时，则下列说法正确

( )

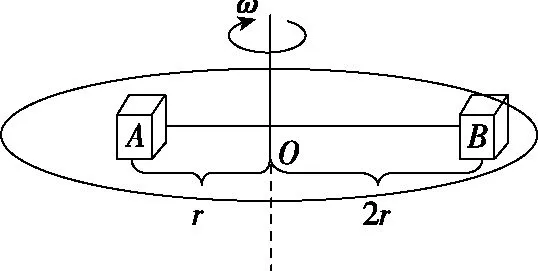
图4

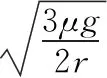
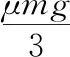
【答案】ACD

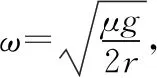
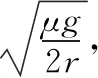
【变式4】如图5所示，在水平圆盘上放有质量分别为m、m、2m的可视为质点的三个物体A、B、C,圆盘可绕垂直圆盘的中心轴OO′转动，三个物体与圆盘的动摩擦因数均为μ=0.1,最大静摩擦力等于滑动摩擦力，三个物体与轴OO′共线且OA=OB=BC=r=0.2 m，现将三个物体用轻质细线相连，保持细线伸直且恰无张力，若圆盘从静止开始转动，且角速度ω缓慢增大，已知重力加速度为g=10 m/s2,则对于这个过程，下列说法正确的是

( )

A.A、B两个物体同时达到最大静摩擦力

B.B、C两个物体的静摩擦力先增大后不变

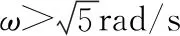
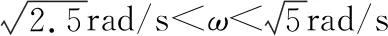
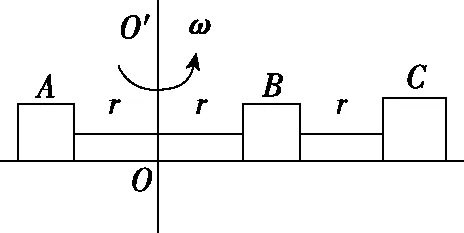
图5

【答案】BCD

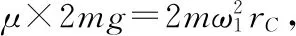
【点评】变式4与变式3相比，牵连体总个数增加，物体的受力情况更加复杂。但是考查的物理思想及解决的方法是类似的。仍然是从受力分析入手，准确找到每个物体做圆周运动向心力的来源，利用隔离法整体法进行分析，通过分类讨论的思想，得到每个物体刚好要相对圆盘发生滑动时对应的临界角速度。难点是分析圆盘角速度缓慢增加过程中，每个物体所受的静摩擦力如何变化，每段绳子拉力如何变化。其中求解整体相对圆盘滑动时圆盘对应的角速度，采用将A、B作为整体来研究处理，使问题变得简单。