基于AFSA-WNN 的Sallen-Key 滤波器电路软故障诊断

王春兰，郭 峰

（西京学院，西安 710123）

0 引言

Sallen-Key 滤波器是1955 年R P Sallen 与E L Key 提出的一种由单个运算放大器和电阻、电容组成的低通滤波器，也是军事装备中应用最广泛的滤波器之一。Sallen-Key 滤波器电路的软故障，存在一定的模糊性和不确定性，难以定位诊断，往往会引起电路和系统性能的恶化，甚至导致系统崩溃，需要对此类故障准确定位和诊断。

针对类似于Sallen-Key 滤波器的模拟电路的软故障诊断问题，目前主要有故障字典法、参数辨识法、故障验证法和神经网络等诊断方法［1-4］。其中，神经网络是一种“黑箱建模”方法，完全颠覆了传统诊断模式，具有较强的学习、识别、记忆和联想功能，然而，其存在精度不高、收敛性差、易局部极小等缺陷［5］。小波神经网络（Wavelet Neural Network，WNN）是基于小波理论的一种前向神经网络［6］，因其理论基础严谨，性能优越，而在相当长的一段时间内，倍受关注和推崇，然而，它也有诸多问题需要解决。在采用WNN 诊断Sallen-Key 滤波器软故障时，WNN 无法提取故障数据的特征，而通常获取的故障数据维数多，受噪声干扰，且各维数据可能彼此相关，会影响模型的诊断精度，因此，在WNN建模前提取故障数据的特征，具有现实意义［7］。此外，在训练WNN 故障诊断模型时，最常用的训练算法为梯度下降法，它是一种局部优化算法，优化时容易收敛到局部极小，导致学习效果不佳，搜索效率不高，因此，需要深入研究更为有效的WNN 训练算法［8］。

基于此，本文引入多分辨率变换特征提取技术与人工鱼群算法（AFSA）优化WNN 方法，以期解决Sallen-Key 滤波器电路的软故障诊断问题。

1 Sallen-Key 滤波器电路的软故障诊断问题

对于如图1 所示的Sallen-Key 滤波器电路，其软故障诊断就是通过某种方法处理故障数据将模拟电路划分为正常状态和故障状态。理论和数值分析表明：1）该电路的输入信号、输出信号和元器件参数都是连续量，理论上有无限种可能的故障，且输入输出关系复杂，除硬故障外，难以构建精确的解析模型；2）该电路的可测试节点数和支路电流难以测量，可供诊断用的故障信息量不足；3）该电路的元器件参数具有容差，即受使用环境等影响，元器件参数会发生随机性漂移，这导致了故障的模糊性，也是故障诊断面临的难点。这些困难使得诸如故障字典、参数辨识、故障验证等传统解析方法无法及时准确地对软故障做出诊断，甚至导致错误的诊断，而基于小波分析与神经网络的“黑箱建模”思想为该电路的软故障诊断问题提供解决思路。

基于此，Sallen-Key 滤波器电路的软故障诊断过程可概括为：首先，通过分析识别出电路元件的故障模式，再执行Monte Carlo 仿真，获得电路故障集；然后，提取各故障模式下输出信号的特征，用于训练模拟电路软故障诊断模型，将待诊断信号相同处理后输入训练好的模型，即可诊断出故障模式。

为简化过程，本文研究Sallen-Key 滤波器的电阻与电容的单个软故障，各元器件的标称值如图1所示，Out 为唯一可测试节点，电容的正常容差范围为10 %，电阻的正常容差范围为5 %。通过软件ORCAD 对Sallen-Key 滤波器电路进行数值仿真，可确定8 种故障模式：R2-、R2+、R3-、R3+、C1-、C1+、C2-和C2+（加上正常模式总共9 种模式），而“+”表示软故障偏大；“－”表示软故障偏小，偏差标称值都为±50%。通过“0-l”方法可描述出9 种模式的期望输出向量［9］，如表1 所示。

图1 Sallen-Key 滤波器

表1 故障诊断系统的期望输出特征

根据以上分析，要采用类似神经网络的“黑箱建模”方法正确诊断Sallen-Key 滤波器电路的软故障，重点需要解决两个问题：一个电路软故障特征的提取问题；另一个电路软故障诊断模型的选择问题。这两个问题中的任何一个解决不好，就不可能得出完全正确可信的诊断结果。

2 基于多分辨率变换的软故障特征提取

Mallat 在构造正交小波基时，最早提出了多分辨率变换的概念，并给出了离散正交二进小波变换的算法［10］，即任何函数f（t）=L2（R）都可根据分辨率为2-N下f 的低频部分（近似部分）和分辨率为2-i（1≤j≤N）下f 的高频部分（细节部分）来实现重构。

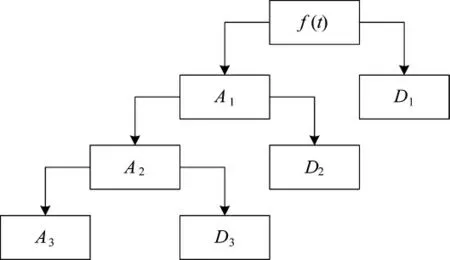
图2 3 层多分辨分析树型结构

分解的关系：f（t）=An+Dn+Dn-1+…+D2+D1，其中f（t）代表信号，D 代表信号分解后高频细节部分，A代表代表信号分解后低频近似部分，n 为所分解的层数。

Sallen-Key 滤波器电路的输出信号中包含丰富的频率成分，发生故障时，这些频率成分受到影响的程度也各不相同，有些得到加强，有些却受到削弱，所以，相同的频率成分在正常时与故障时会表现出一定的差异，使同一成分的小波系数也发生变化。由此可知，Sallen-Key 滤波器电路的输出信号包含着丰富的故障信息，将输出信号中的一些频率成分的变化提取出来，就可表征一个故障，进而成为模型的输入量。采用多分辨率变换提取Sallen-Key滤波器电路的输出信号特征的优点：小波方差运算简便，抗干扰性能好，主要挖掘数据及共蕴涵信息的普适量，能够有效刻画各种尺度信号的特征，避开了对小波系数的繁琐处理。

综上所述，多分辨率变换的软故障特征提取步骤如下：

1）对电路故障采样信号f（t）进行n 尺度多分辨率分解；

2）提取各层高频系数序列D1，D2，…，Dj，…，Dn和第n 层的低频序列An；

3）令Ei为高频序列Dj中各分量的平方和，称为第i 层的高频能量i =1，…，j，…，n，令E0为低频序列An的平方和，称为第n 层的低频能量；

4）把n+1 维向量{ E0，E1，…，Ej，…，En}归一化后，结合期望输出向量，即获得Sallen-Key 滤波器电路的故障特征样本集。

3 基于AFSA 的WNN 软故障诊断模型

3.1 人工鱼群算法及其混沌初始化策略

AFSA 通过模仿鱼的运动、聚集等行为构造人工鱼，利用觅食、聚群及追尾行为自适应调整自身位置，经过一段时间后，各人工鱼在各极值处聚集，并通过局部寻优搜索全局最优值［11］。

研究表明，AFSA 具有出色的全局搜索能力，是解决最优化问题的重要工具。然而，在实践应用中，AFSA 可能陷入局部极优，进而导致搜索效率低下。理论研究与数值仿真表明，采用AFSA 优化搜索过程中，人工鱼群的随机初始化策略存在一定的弊端。尽管这种策略产生的初始鱼群大多是分布均匀的，但仍然无法保证部分个体远离最优解。如果利用某种方法改进随机初始化策略，将有助于求解效率和解的质量。基于此，本文引入了混沌初始化策略。

混沌具有丰富的时空动态，其不同于混乱和无规律现象，混沌现象虽然貌似随机现象，却有着精致的内在结构，且表现出随机性、遍历性和规律性。尤其是遍历性，它能够在特定范围内按照其自身规律不重复地遍历所有状态，这种遍历性特点可使搜索过程中避免陷入局部极值。因此，在AFSA 的鱼群初始化阶段引入混沌，可使鱼群摆脱局部极值点的束缚，提高全局收敛性和搜索效率［12］。本文采用的混沌系统是由Logistic 映射产生的，该映射计算量小、使用方便，应用广泛，其时间序列可定义为

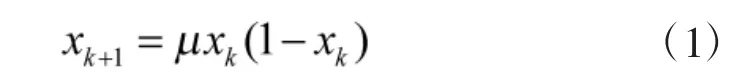
式中，x∈（0，1），分岔参数μ=［1，4］。当μ=［3.569 94，4］时，系统处于混沌区域，在此区域内映射方程运动轨迹表现出混沌特性。

3.2 小波神经网络

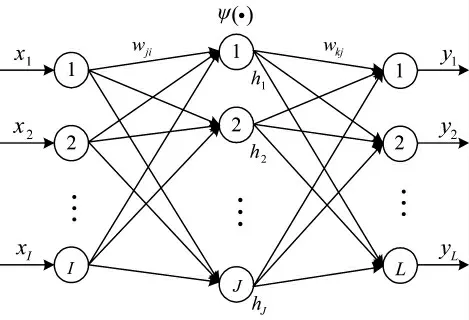
图3 WNN 的基本结构

在如图3 所示的WNN 结构中，输入节点为xi（i=1，2，…，I），隐节点输出为hj（j=1，2，…，J），输出节点为yl（l=1，2，…，L）；输入层与隐含层之间节点的连接权值为wji（j=1，2，…，J；i=1，2，…，I），隐含层至输出层之间节点的连接权值为wlj（l=1，2，…，L；j=1，2，…，J）；伸缩因子为aj（j=1，2，…，J）或平移因子为bj（j=1，2，…，J）；ψ（·）为小波基函数；I 为输入节点数，J 为隐节点数，L 为输出节点数。

从最优估计理论来说，WNN 训练过程实际上就是通过某种优化算法获取最优参数wji，wlj，aj，bj组合的过程，而不同的优化算法，自然就构成不同的WNN 训练算法。

3.3 AFSA-WNN 建模步骤

考虑到WNN 的常用BP 算法的局限性，本文引入AFSA 训练如图3 所示的WNN，则WNN 各参数的编码为人工鱼向量X，即人工鱼的每个维度对应WNN 的一个wji，wlj，aj，bj。将下式设置为适应函数

式中，p 为样本总数。需要说明的是，此时AFSA 的WNN 参数优化搜索空间的维数为D=I×J+J×L+2J。

设用于混沌初始化策略的人工鱼个体数Nc、鱼群大小N、目标精度ε、视野Visual、移动步长Step、觅食尝试次数Trynumber、拥挤度因子δ、最大迭代次数MaxNum、初始迭代次数Num=0。参数wji，wlj，aj，bj在区间［0，1］内编码，并通过式（1）的Logistic映射方程生成Nc人工鱼个体，并取N（＜Nc）相对优良个体组成初始化鱼群。AFSA-WNN 的训练流程如图4 所示。

图4 AFSA-WNN 的训练流程

算法终止后，对公告板中的人工鱼进行解码，即得对应WNN 参数wji，wlj，aj，bj的最优组合，训练完成。

4 实例仿真

仿真环境：Pentium IV 2.4 GHz CPU，内存4 GB DDR，硬盘80 GB+7 200 转；Windows 7 操作系统。本文算法采用软件MATLAB 编程实现并仿真测试。

4.1 软故障特征提取

在图1 所示的Sallen-Key 滤波器中，输入Vin为幅值4 V、频率1 kHz 的正弦波激励。扫描步长0.5μs，扫描的时段0.25 ms～1.5 ms，将软件ORCAD中的电路特性分析设定为瞬态分析，并执行Monte Carlo 模拟。图5 给出了R2-与R2+的正常模式与故障模式输出对比，其中，实线代表故障信号的输出端电压频率响应波形。通过对各故障模式与正常模式分别进行50 次仿真，可以分别得到各故障模式与正常模式下输出的50 个瞬态响应信号波形，并将采集到的波形数据保存到输出文本文件中。这样，可以在0.25 ms～1.5 ms 时段内得到9×50 个信号。

在提取信号特征时，可以选取db2 小波为小波基函数，主要原因是，dbN 小波满足正交性、正则性和紧支撑条件，且时频局域性好，能够更精确地描述信号的本质特征。而在dbN 小波中较为常用的db2、db3 和db5 小波中，尤以db2 提取信号特征的效果最好。对9×50 个信号数据作5 层多分辨率分解，得到一个低频系数序列A 和5 个高频系数序列D1、D2、D3、D4、D5和D6，并计算各系数序列的能量，归一化处理后，与相对应的期望输出，构成9×50组特征样本，并随机取180 组作为训练样本，余下的作为测试样本。

4.2 软故障建模诊断

将获取的训练样本输入AFSA-WNN，即可训练出模拟电路的软故障诊断模型，并可用测试样本进行验证。在本文实验中，假设如果WNN 任一输出节点的输出与期望输出之差的绝对值小于0.3 （判定值可视情况取值），可认定为诊断正确；否则，可认定为诊断错误。

参数设置：Nc=100，N=40，Visual=2.85，MaxNum=200，Trynumber=20，Step=0.25，δ=0.618，根据经验参考公式，隐含层节点个数可取10，可计算出搜索空间维数D=190。通过训练和测试后，表2 和3 对比了WNN（BP 算法）和AFSA-WNN 两种模型的训练及测试结果，其中，C 表示正确诊断数；R 表示正确诊断率，而图6 对比了两种模型训练的收敛性能。

表2 诊断模型的训练和测试性能对比

表3 测试样本诊断结果对比

图6 训练收敛曲线对比

从软故障实验结果可以看出，与WNN 相比，AFSA-WNN 训练和测试效果更好，其仅通过60 多次迭代训练，就收敛到一个较为满意的水平，诊断的总正确率也达到94.1%，而各单项测试结果中，除模式R3-的正确率诊断率略低外，其他模式都比WNN 有了显著提高，模式R3-和正常的正确诊断率甚至达到了100%，据此，可认定得到的软故障诊断模型比较令人满意。这说明基于多分辨率变换的软故障特征提取与AFSA-WNN 的软故障诊断技术，确实能够有效降低由电路元器件容差引起的诊断偏差，也验证了采用本文方法用于Sallen-Key 滤波器电路软故障诊断的可行性和有效性。

5 结论

针对Sallen-Key 滤波器电路中因元器件容差导致故障难以诊断的难题，提出基于多分辨率变换特征提取与AFSA-WNN 的软故障诊断方法。它采用多分辨率变换提取电路的软故障特征，并在此基础上构建AFSA-WNN 软故障诊断模型，以期改善诊断精度。仿真结果表明，基于多分辨率变换特征提取与AFSA-WNN 的软故障诊断方法，单项和总体诊断正确率高，各项性能明显优于单纯的WNN，较好解决了容差导致故障难以检测的问题。从而说明本文方法用于Sallen-Key 滤波器电路的软故障诊断是有效和可行的。