基于复相关系数的时滞联合估计及其应用

李海军　夏静　史恒惠　刘长良　王梓齐

摘要：针对工业过程的软测量建模，为对输入与输出变量间的时滞关系进行准确、快速地估计，提出一种基于复相关系数的时滞联合估计方法。该方法以模型输入和输出数据间的复相关系数为指标，将时滞联合估计问题转化为多维优化问题，进而对各输入变量的时滞时间进行寻优。针对火电厂脱硝系统的NO，排放软测量，基于实际的运行数据和最小二乘支持向量机算法，对所提出的方法进行验证并与其他时滞估计方法进行对比。结果表明：基于复相关系数的时滞估计方法计算速度较快，时滞估计结果较准确，能在一定程度上提高软测量模型的准确度。

关键词：复相关系数;时滞联合估计;NO_x排放;软测量

中图分类号：TP206 文献标志码：A 文章编号：1674-5124（2019）08-0140-05

收稿日期：2018-07-16;收到修改稿日期：2018-09-04

基金项目：北京市自然科学基金资助项目（4182061）

作者简介：李海军（1973-），男，河南焦作市人，工程师，研究方向为火电机组软测量、远程诊断。

0 引言

工业过程的软测量建模，除了受辅助变量选取、建模方法等因素的决定外，辅助变量与主导变量间的时滞关系同样会对模型准确度产生一定的影响[1]。若不考虑辅助变量的时滞，会在一定程度上对模型的准确度产生负面影响。对于复杂的生产过程，很难通过机理分析确定具体的时滞时间。因此，在实际应用中多采用数据驱动方法估计辅助变量的时滞时间，主要分为单变量估计和联合估计两种。

单变量估计独立地分析每个辅助变量与输出变量间的时滞关系，有着便于实现、计算速度快等优点。文献[2]基于相关系数确定时间序列模型中的最优时滞因子并应用于交通流量的预测。文献[3]基于归一化互信息确定聚丙烯熔融指数预测模型中各自变量的时滞时间。文献[4]提出了一种基于模糊曲线分析的单变量时滞估计方法。文献[5]将模糊曲线分析时滞估计与选择性集成高斯过程回归算法进行结合，建立了脱丁烷塔底浓度的软测量模型。但是，单变量估计在计算时中忽略了其他辅助变量对输出的影响以及辅助变量之间的相互影响，有可能会导致估计结果的不准确。

联合估计综合考虑各辅助变量与输出间以及各辅助变量之间的关系从而确定时滞时间。文献[6]以所有辅助变量和主导变量间的联合互信息作为目标函数对时滞时间进行寻优。文献[7]以软测量模型的训练误差作为目标函数，使用混合差分进化算法对时滞时间进行寻优。文献[8]使用差分进化算法对时滞时间进行寻优，并结合偏最小二乘算法，建立了常压塔干点的软测量模型。但是，由于需要计算联合互信息等复杂函数或需要对模型进行训练，时滞联合估计在输入维数高、样本数量大的情况下往往运算时间较长，不利于实际的工程实践。

复相关系数是反映一个因变量与一组自变量之间相关程度的指标[9]，其常应用于多元相关分析、多元线性回归的评价等数理统计领域，文献[10-11]将复相关系数应用于确定数据包络分析中自变量与因变量间的时间滞后关系。复相关系数是通过对输入、输出数据进行线性拟合进而计算得到的，相比于联合互信息或训练数据驱动模型，其计算速度有明显的优势。

因此，本文提出了一种基于复相关系数的时滞联合估计方法。该方法以辅助变量和输出变量间的复相关系数为指标，将时滞估计转化为多维优化问题进行求解，有着计算快、准确度高的特点。以火电厂脱硝系统NO_x排放浓度的软测量为例，基于实际运行数据对所提出方法进行了验证。

1 基于复相关系数的时滞联合估计

1.1 过程变量的时滞估计

传统的软测量建模中往往不考虑辅助变量的时滞问题，多直接使用同一采样时刻的辅助变量和输出变量数据建立模型。但对于工业过程特别是化工、冶炼、发电等相关领域，从工艺流程到测量仪表等环节均存在较大的时滞。因此，有必要在建模过程中考虑各辅助变量的时滞，从而进一步提高软测量模型的准确度。

考虑辅助变量时滞的软测量模型结构如下：

y（t）=f[x₁（t-τ₁），x₂（t-τ₂），…，x_n（t-τ_n）]（1）式中：y（t）——软测量模型的输出变量;

x_k（t-τ_k）——模型的辅助变量;

τ_k——辅助变量x_k的时滞时间。

辅助变量的时滞估计是采用机理分析或数据驱动方法，计算辅助变量的时滞时间τ。对于复杂的工业过程，很难使用机理分析方法精确计算各输入变量的时滞时间，常用数据驱动方法进行时滞估计。

数据驱动时滞估计方法的基本思想是将同一采样时刻的历史输入数据X（t）∈Rⁿ进行时序重构，得到新的输入数据X_d（t）=[X₁（t-τ₁），X₂（t-τ₂），…，X_n（t-τ_n）]^T。

之后基于某一给定的指标（如互信息、相关系数等）确定最优的时滞时间。数据驱动时滞估计方法主要分为单变量估计和联合估计两种。

单变量时滞估计独立地分析单个辅助变量与输出间的时滞关系，即将时滞估计问题转化为如下的优化问题：其中，f₁可为相关系数、互信息等目标函数。

单变量时滞估计通过数个一维优化问题进行求解，计算速度相对较快。但在寻优时仅考虑某个辅助变量与输出的关系而忽略了其他辅助变量与输出的关系以及辅助变量之间的关系，存在一定的片面性，可能会在一定程度上导致估计结果的不准确，从而影响软测量模型的準确度。

時滞联合估计方法综合考虑各辅助变量与输出以及各辅助变量之间的关系，对各辅助变量的时滞时间进行联合寻优，即转化为如下的优化问题：其中，f₂可为联合互信息、软测量模型训练误差等目标函数。

时滞联合估计通过多维优化问题进行求解，相比于单变量估计从理论上更为准确。但是，联合估计在寻优过程中需要计算联合互信息等复杂函数或需要对软测量模型进行训练，在输入维数高、样本数量大的情况下耗时较长，不利于工程实践。

1.2 复相关系数及其在时滞估计中的应用

复相关系数R越大，表明因变量和该组自变量间的线性相关程度越大。复相关系数R通常使用以下步骤进行计算：

1）使用时序重构后的输入数据X_d（t）和输出数据Y（t）进行多元线性回归。

2）基于线性模型计算预测諽Y（t）。

3）计算实际值Y（t）和预测值Y（t）之间的简单相关系数，即为Y（t）和X_d（t）间的复相关系数R，具体的计算公式如下：其中，Y为实际值Y（t）的算术平均值。

除上述步骤外，复相关系数R也可以通过X_d（t）和Y（t）多元线性回归后得到的决定系数R²开方得到。

基于复相关系数进行时滞联合估计，即求解如下规划问题：其中，由于时滞时间应为采样间隔的整数倍，故其定义域应为自然数域N;T为时滞时间的上界。

上述规划问题是非线性整数规划问题，可采用分支定界法或启发式算法进行求解。启发式算法的结构较为简单、计算速度较快，但无法方便处理复杂的约束条件。由于以上规划问题不含等式、非线性等复杂的约束条件，可使用启发式算法进行求解。

相比于单变量时滞估计，复相关系数在计算时充分考虑了自变量间的相关关系，估计结果相对更为准确;相比于其他时滞联合估计方法，进行多元线性回归所需要的时间要远小于计算联合互信息或训练软测量模型，实时性相对较好。因此，从理论上讲，基于复相关系数的时滞联合估计能够更好地平衡估计结果的准确性和计算的快速性。

2 复相关系数时滞联合估计在软测量中的应用

2.1 火电厂脱硝系统及NO_x排放软测量

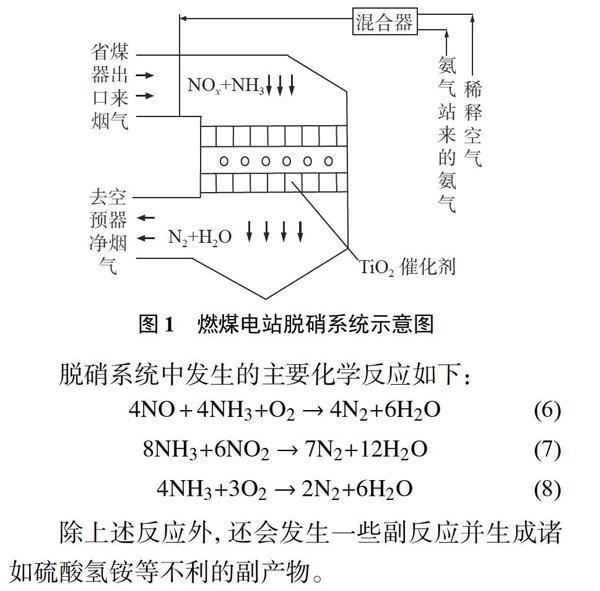
图1为火电厂脱硝系统工艺流程的示意图。脱硝系统布置在锅炉的省煤器与空预器之间，其基本工作过程如下[12]：氨气与风机送来的空气进行混合后通过喷嘴进入烟道，与省煤器出口来的烟气充分混合后进入反应器，在催化剂的催化作用下发生还原反应，将烟气中的NO_x还原为氮气与水蒸气。

脱硝系统中发生的主要化学反应如下：

4NO+4NH₃+O₂→4N₂+6H₂O（6）

8NH₃+6NO₂→7N₂+12H₂O（7）

4NH₃+3O₂→22+6H₂O（8）

除上述反应外，还会发生一些副反应并生成诸如硫酸氢铵等不利的副产物。

由于脱硝系统中气体分析仪表的测量滞后较大且需要频繁进行吹扫，导致传统的控制策略往往难以长时间精确地控制喷氨量。喷氨量偏少会导致NO_x排放超标，而过量喷氨除了会导致经济上的损失外，还会造成催化剂寿命缩短、下游设备堵塞、氨逃逸率增大等不良后果。因此，有必要建立准确的NO_x排放浓度软测量模型以进一步实现喷氨量的闭环优化控制。

一般情况下，考虑辅助变量时滞估计的软测量建模步骤如下：

1）根据过程机理以及现场实际测点情况，确定与输出变量密切相关的辅助变量。

₂）获取相应的运行数据并进行去离群点、滤波、归一化等预处理操作，之后确定软测量模型的训练样本和测试样本。

3）基于训练样本以及相应的时滞估计方法，确定各辅助变量的时滞时间并对训练、测试样本进行时序重构。

4）基于选定的软测量建模方法，使用时序重构后的训练、测试样本对软测量模型进行训练和测试。

2.2 辅助变量选取及数据预处理

结合2.1中的机理分析及数据库中实际的测点情况，同时考虑机组负荷变化对脱硝过程产生的影响，选择脱硝系统入口 NO_x浓度、入口烟气含氧量、出口烟气含氧量、烟气流量、入口烟气温度、喷氨量和机组负荷共7个变量作为软测量模型的辅助变量，输出变量为脱硝系统出口的NO_x浓度。

从数据库中导出一段变负荷工况下的运行数据，采样间隔为10s，共1200组。基于拉依达准则剔除离群点，之后基于滑动窗口法进行滤波。剩余1067组数据并从中选取1000组数据进行归一化后参与软测量建模，选择前800组数据作为训练样本，后200组数据作为测试样本。归一化前建模数据中各变量的变化范围如表1所示。

2.3 基于复相关系数的辅助变量时滞估计

考虑到脱硝系统中气体分析仪表的响应时间一般为30～120s，故设定各辅助变量时滞时间的上界T=120s。为对比各时滞估计方法在估计结果上的不同，同时基于复相关系数法、相关系数法和联合互信息法对7个辅助变量进行时滞估计。相关系数法使用枚举法进行求解，复相关系数法和联合互信息法均用遗传算法求解。遗传算法的种群规模设置为20，迭代次数为100。

各方法时滞估计的结果如表2所示。相关系数法计算耗时0.05s，复相关系数法耗时1.%s，联合互信息法耗时51.46s。

从表中可以看出，复相关系数法和联合互信息法的时滞估计结果较为接近，而与相关系数法存在一定的差异。从机理上分析，入口NO_x浓度和烟气含氧量这两个测点均位于脱硝系统的入口处且使用同一气体分析仪表进行测量，其与输出变量的时滞关系应基本一致;而出口烟气含氧量和出口NO_x浓度的测点位置和测量仪表均相同，两者间应不存在时滞关系。因此，复相关系数法和联合互信息法的估计结果要比相关系数法更具有准确性。同时结合3种算法的计算时间，相比于相关系数法和联合互信息法，复相关系数法时滞估计的准确性和计算速度均较快，有着一定的优势。

3 实验结果及分析

火电厂的NO_x排放浓度常用人工神经网络[13]、最小二乘支持向量机[14]等智能方法建立软测量模型。相比于人工神经网络等机器学习方法，最小二乘支持向量机（least square support vector machine，LS-SVM）有着泛化能力较强、能够收敛至全局最优点、训练速度较快的优点。因此，本文选择LS-SVM算法建立NO_x排放的软测量模型。

LS-SVM的实现基于Matlab的LS-SVM工具箱，选择LS-SVM的核函数为线性函数，参数训练选择贯序最小优化（sequentialminimal optimization，SMO）算法。基于LS-SVM分别建立不进行辅助变量时滞估计和使用复相关系数法进行时滞估计两种情况下的NO_x排放软测量模型。两个模型预测值与实际值的对比以及预测残差间的对比如图2和图3所示。

如图2和图3所示，使用复相关系数进行时滞估计后，软测量模型的准确度和跟踪能力均要显著优于无时滞估计的模型，说明引入辅助变量的时滞信息能有效提高软测量模型的准确度。

为了比较各时滞估计方法对模型准确度的影响，分别基于相关系数法和联合互信息法的时滞估计结果建立软测量模型，并在测试样本上与不进行时滞估计和复相关系数法进行比较，结果如表3所示。其中RMSE为模型在测试样本上的均方根误差， MRE为模型在测试样本上的平均相对误差。

由表可知，进行辅助变量时滞估计后，模型的准确度都有着一定程度的提高，而相关系数法准确度提高的程度要小于联合互信息法和复相关系数法，与1.1中对单变量估计和联合估计方法的理论分析以及2.3中基于测点位置的机理分析结果相一致。

4 结束语

本文提出了一种基于复相关系数的辅助变量时滞联合估计方法并将其应用于火电厂脱硝系统的NQ排放软测量中。基于变负荷工况下的实际运行数据，结合LS-SVM算法对所提出的估计方法进行了验证，并与不进行时滞估计、相关系数法和联合互信息法进行了对比。结果表明，进行时滞估计后软测量模型的准确度有了一定的提高且相比于其他时滞估计方法，所提出方法的计算速度较快、估计结果较准确，有着更好的工程应用价值。

参考文献

[1]XIONG W，LI Y，ZHAO Y，et al.Adaptive soft sensor basedon time difference Gaussian process regression with localtime-delay reconstruction[J].Chemical Engineering Research&Design，2017，117：670-680.

[2]申贵成，管水城，孙方宇.考虑最优时滞因子时空模型的高速公路短时交通流预测[J].科学技术与工程，2018，18（24）：149-156.

[3]LOU H，SU H，XIE L，et al.Inferential model for industrialpolypropylene melt index prediction with embedded prioriknowledge and delay estimation[J].Industrial&EngineeringChemistry Research，2012，51（25）：8510-8525.

[4]李妍君，熊偉丽，徐保国一种带过程变量时滞估计的在线软测量建模方法[J].信息与控制，2016，45（6）：641-646.

[5]熊伟丽，李妍君.选择性集成LTDGPR模型的自适应软测量建模方法[J].化工学报，2017，68（3）：984-991.

[6]阮宏镁，田学民，王平.基于联合互信息的动态软测量方法[J].化工学报，2014，65（11）：4497-4502.

[7]王钧炎，黄德先.基于混合差分进化算法的软测量时延参数估计[J].化工学报，2008，59（8）：2058-2064.

[8]阮宏镁，田学民，王平.带时延估计的时间差分PLS软测量建模方法[J].石油化工自动化2013，49（6）：35-39.

[9]MONDINI V，MANGIA A L，TALEVI L，et al.Sinc-windowing and multiple correlation coefficients improveSSVEP recognition based on canonical correlationanalysis[J].Computational Intelligence and Neuroscience，2018，2018：4278782.

[10]管燕，吴和成，黄舜.基于改进DEA的江苏省科技资源配置效率研究[J].科研管理，2011，32（2）：145-150.

[11]范德成，李昊，刘贇.基于改进DEA——以复相关系数为基准的滞后期的我国产业结构演化效率评价[J].运筹与管理，2016，25（3）：195-203.

[12]秦天牧，吕游，杨婷婷，等.SCR烟气脱硝系统自适应混合动态模型[J].仪器仪表学报，2016，37（12）：2844-2850.

[13]马平，李珍，梁薇.基于互信息的辅助变量筛选及在火电厂NO_x软测量模型中的应用[J].科学技术与工程，2017，17（22）：249-254.

[14]丁续达，刘潇，金秀章.基于压缩感知最小二乘支持向量机的NOx软测量模型[J].热力发电，2018，47（3）：76-81.

（编辑：商丹丹）