精确型傅里叶高度函数描述子的服装款式识别方法

孙国栋　徐亮

摘要：针对服装款式自动识别时存在提取特征困难、识别率低和分类效率低等问题，该文在精确型傅里叶高度函数（accurate Fourier height functions 2，AFHF2）与线性核函数支持向量机（support vector machine，SVM）基础上提出一种新的服装款式识别方法。首先，利用AHFH2描述子对衣服轮廓进行特征提取，对服装轮廓全局信息和局部信息进行充分表征;然后，在不需要调整参数的情况下使用线性核函数SVM对AFHF2描述子特征进行快速训练与测试。通过自建的服装图形库验证该方法的有效性，实验结果表明该算法优于现有的算法，其中AFHF2描述子优于傅里叶描述子、高度函数（HF）和TCDs等算法，线性核函数SVM算法优于径向基函数SVM算法、K-近邻算法、概率神经网络以及反向传播神经网络算法，其平均识别率能达到97.91%。

关键词：精确型傅里叶高度函数;支持向量机;服装款式识别

中图分类号：TS941.26 文献标志码：A 文章编号：1674-5124（2019）08-0130-05

收稿日期：2019-01-17;收到修改稿日期：2019-03-29

基金项目：国家自然科学基金项目（51775177，51675166）

作者简介：孙国栋（1981-），男，湖北天门市人，教授，博士，主要从事图像处理和机器学习方面的研究。

0 引言

随着社会发展与生活节奏加快，网购服装由于其便捷性成为主流的服装购买方式，购买量逐年增加。快速检索顾客的理想服装款式成为相关行业的研究热点，而服装款式识别是服装检索的前提[1]。

服装款式是由服装的外部轮廓和内部细节变化构成的，反映了服装结构的形状特征，不包含颜色和纹理特征[2]。在一些研究中服装识别被视为一种二维图像的模式识别，正确判断图像的类别是服装识别的前提。

特征提取是服装识别的关键步骤，已有学者提出多种服装特征提取方法，如轮廓曲率特征点[3]、傅里叶描述子（Fourier descriptors，FD）[4]、HOG（histogramof oriented gradient）和几何特征[5]、融合多层次特征[6]等。其中，轮廓曲率特征点方法特征向量维度低，但是其抗噪性能差，忽略了过多局部信息，识别率不高;FD提取特征能够表征服装轮廓信息，但是提取特征算法简单，当样本复杂程度增加时，其表征能力将会一定程度的降低;HOG和几何特征与融合多层次特征算法表征能力有限，且算法较复杂，通用性较差。

精确型傅里叶高度函数描述子（accurate Fourierheight functions 2，AFHF2）[7]是一种具有起始点不变性、相似不变性、抗噪性、低维度等特点的轮廓描述子，能够对轮廓的全局信息和局部信息进行充分表征，且计算复杂度低，适合服装款式的实时识别。

分类器的选择是服装款式识别的另一关键步骤。支持向量机（support vector machine，SVM）[3-4]、K一近邻算法（K-nearest neighbor，KNN）[8]，概率神经网络（probabilistic neural networks，PNN）[9]以及反向传播神经网络（back propagation neural network，BPNN）[10]是常用的特征分类器，但是每个分类器适用的分类矩阵和样本量是不同的，其中SVM分類器更适合小样本分类，广泛应用于服装款式分类。SVM所使用的核函数决定分类器的性能，现有的服装款式涉及的SVM分类器大部分采用径向基核函数。而径向基核函数SVM分类器的惩罚参数和核函数的寻优问题一直没有得到很好的解决，其参数寻优过程非常耗时。线性核函数SVM不需要调参过程，且识别速度快，识别率与径向基核函数SVM相当，更适合服装款式实时识别。

因此本文结合AFHF2和线性核函数SVM的优点，提出一种新的服装款式识别方法，即利用AFHF2描述子提取服装轮廓特征，然后在不调参的情况下，使用线性核函数SVM对提取的AFHF2特征进行训练和测试，达到服装款式实时识别的要求。

1 基于AFHF2与SVM的服装款式识别方法

1.1 AFHF2描述子

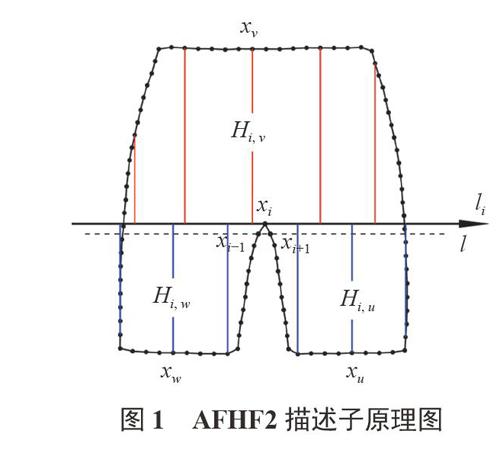
AFHF2是一种基于轮廓信息的形状描述子，它能准确表征轮廓的全局信息和局部信息[7]，其原理如图1所示。

S={x_i}（i=1，2，3，…，N）为目标轮廓采样点集，其中N为采样点总数，x_i表示轮廓上第i个点。由图1可知，过点x_i做直线L的平行线l_i，作为基准轴，消除原高度函数使用直线l作为基准轴产生的高度误差，其中l是过点x_i-1和x_i+1的直线。按照采样点的顺序依次计算出其他采样点到基准轴的高度值，组成x_i对应的高度特征向量：式中H_ij表示第j个采样点相对于x_i参考点的高度值，即x_j到l_i的垂直距离。H_i，u，H_i，v，H_i，w分别表示点x_u，x_v，x_w相对于点x_i的高度值。依次求出所有样本点的高度特征向量，得到轮廓S的高度特征矩阵。

然后，对高度特征矩阵进行平滑化处理[11]和行归一化[12]处理，使得描述子获得紧凑性和缩放不变性;最后，对归一化后的特征矩阵每一行进行傅里叶变换。用AHFi表示经过平滑化和归一化处理后高度特征矩阵的每一行，其中i=1，2，…，M。AHF_i的离散傅里叶变换如下所示：式中t=1，2，…，H，H为傅里叶阶数;AHF_i（u）表示高度特征矩阵傅里叶变换前的第i个行向量的第u列元素。abs（F_i（t））是F_i（t）的绝对值，表示离散傅里叶变换系数F_i（t）的模量，经过证明abs（F_i（t））对形状轮廓的起始点是不变的[13]。

最终AFHF2描述子矩阵定义如下：式中i=1，2，…，M;v=1，2，…，H;F_i（v）表示离散傅里叶变换系数;M为经过平滑化处理后高度矩阵的行数;H为傅里叶阶数。

AFHF2描述子具有良好的起始点不变性、相似不变性、抗噪性、低维度等特点，对轮廓的全局信息和局部信息进行充分表征，且计算复杂度低，能够达到服装款特征提取的要求。

1.2 服装款式识别算法流程图

结合AFHF2描述子与线性核函数SVM在分类上的优势，设计了一种新的服装款式识别方法，其具体流程如图2所示。

首先，将服装款式图形样本随机分成训练样本和测试样本;然后，按照文献[3]方法对所有样本进行预处理，即先灰度化处理、灰度增强和二值化处理，再提取出预处理后服装图形的最大外轮廓线、选取采样点以及计算AFHF2特征;再将训练样本提取出来的AFHF2特征用于训练线性核函数SVM模型;最后，使用训练好的SVM模型对服装图形测试样本分类，得到最终的服装款式识别结果。

2 实验与结果分析

为了验证所设计的服装款式识别方法的性能，本文建立了一个包含10类服装款式的样本库进行实验，并将通用形状描述子HF（height function）[11]、TCDs（triangular centroid distances）[4]和文献[4]提出的FD与本文使用的AFHF2描述子对比，用BPNN、PNN、KNN、径向基核函数SVM与本文采用的线性核函数SVM分类器对比。

2.1 服装款式库

由于现有的服装款式库的样本种类数和样本量都较小，且样本复杂度低，与实际应用相差较大，本文搜集整理淘宝网10种款式的服装，包括衬衫、短裤、短裙、短袖T恤、短袖连衣裙、西装、长裤、长袖T恤、长袖连衣裙和外套，其中每类服装款式的样本量为250张，且样本复杂度高，部分样本款式如图3所示。

2.2 服装款式识别实验

按照图2服装款式识别流程对本文制作的服装款式库进行识别实验。每类样本随机提取出150张样本作为训练样本，剩余的100张样本作为测试样本。本文所有结果由10次实验取平均值后得到。

实验使用的线性核函数SVM来自LIBSVM[14]工具包，且线性核函数SVM不需要调整其他参数。另外，实验使用的AFHF2描述子参数设置如下：每个样本的轮廓采样点个数为100。平滑化系数k决定了描述子的抗噪性能，由图4可知，k取3时，识别率最高，即k取最优值为3。

每一款服装的识别结果如表1所示。结合图4和表1的实验结果可知，每一款服装的识别率都超过96.22%，平均识别率达到97.91%，能够达到较高的准确率。另外，长袖T恤、外套以及西装这4款在外形上较为相似，但是其识别率仍然在96.22%以上，能够达到识别要求。

2.3 对比实验与结果分析

为了进一步验证所设计服装款式识别方法在特征提取和分类方面的优势，本文采用现有识别效果较好的FD提取方法以及现有通用轮廓描述子-HF和TCDs描述子与本文使用的AFHF2描述子对比，用广泛使用的径向基函数SVM、KNN、PNN以及BP神经网络与本文使用的線性核函数SVM对比。

2.3.1 服装款式特征提取性能对比实验

本文分别使用AFHF2、FD、IT、TCDs描述子作为特征提取描述子进行实验，采用线性核函数SVM对2.1节的服装样本库进行训练和测试，其中训练样本和测试样本分别占总样本的60%和40%;所有描述子的轮廓采样点个数都为100;FD的参数设置同文献[4]，即特征向量长度设置为20; TCDs描述子参数设置同文献[11]，即傅里叶系数的阶数设置为160对比实验结果如表2所示。

由表可知，4种描述子的训练时间和单个样本的测试时间相差不大。但是，从识别率角度看，AFHF2描述子的识别率最高，达到了97.91%。说明AFHF2描述子更适合服装款式轮廓特征提取。

2.3.2 多种分类器对比实验

径向基核函数SVM、KNN、PNN以及BPNN是近年来应用较为广泛的机器学习方法。因此采用以上4种方法与本文使用的线性核函数SVM对比，对2.2节实验提取的AFHF2特征进行识别，选取其中60%样本训练，另外40%样本测试，其实验结果如表3所示。

各方法的参数主要通过多次实验取最优值得到，其中径向基核函数SVM的参数通过网络搜索参数寻优方法[I S]获得，各参数设置如下：

1）径向基核函数SVM的惩罚系数。和核参数Y分别设置为1048576和9.536×10^-7;

2）PNN的平滑参数设置为2;

3）KNN距离度量方式设置为欧几里得距离，k值设置为5;

4）BPNN的隐含层节点设置为30，学习率设置为0.01，训练要求精度设置为0.0001，训练周期设置为1000。

由表3实验结果可知，线性核函数SVM识别率高于径向基核函数SVM、PNN、KNN以及BPNN。BPNN采用梯度下降法，有可能会进入局部最小值而训练失败，网络识别率波动较大，导致平均识别率较低。PNN结构简单，其中平滑因子对于识别结果的影响较大，且对样本的代表性要求较高。KNN识别效率较低，虽然没有训练过程，但每次测试都需要将测试样本和所有训练样本计算一遍，且对训练样本要求高。SVM更适合小样本分类，少数样本即可决定最终结果，对样本要求相比BPNN、PNN和KNN低，识别率更高。径向基核函数SVM的识别率与线性核函数SVM接近，而径向基核函数SVM需要参数寻优，增加了模型的训练时间，其训练时间是线性核函数SVM模型的2.45倍。因此，线性核函数SVM比径向基核函数SVM、PNN、KNN、BPNN更适合服装款式识别。

3 结束语

本文使用AFHF2描述子提取服装的轮廓特征，再使用线性核函数SVM对特征进行分类与测试，实现了一种新的服装识别的方法。通过对十类复杂的服装样本库进行测试发现：AFHF2描述子能准确表达服装轮廓特征，优于现有的FD、HF和TCDs描述子;SVM对于AFHF2的特征分类效果好，优于径向基核函数SVM、PNN、KNN和BPNN，具有较高的实用价值。

由于本文实验所用样本的背景颜色单一，后期将采集更为复杂的自然条件下服装图片进行实验。

参考文献

[1]GUPTA M，BHATNAGAR C，JALAL A S.Clothing imageretrieval based on multiple features for smarter shopping[J].Procedia Computer Science，2018，125：143-148.

[2]燕平.服裝款式设计[M].重庆：西南师范大学出版社，2011：3-4.

[3]李东，万贤福，汪军，等.基于轮廓曲率特征点的服装款式识别方法[J].东华大学学报（自然科学版），2018，44（1）：87-92.

[4]李东，万贤福，汪军.采用傅里叶描述子和支持向量机的服装款式识别方法[J].纺织学报，2017（5）：122-127.

[5]纪娟，纪娟，秦珂，等.基于HOG和几何特征的服装细节要素识别与分类[J].图学学报，2016，37（1）：84-90.

[6]于雨桐.基于多特征融合的服装图像款式识别的研究与应用[D].北京：北京工业大学，2016.

[7]WU B，FENG S L，SUN G D，et al.Identification method ofshaft orbit in rotating machines based on accurate fourierheight functions descriptors[J].Shock and Vibration，2018（3737250）：1-10.

[8]李霁蒲，赵荣珍.近邻概率距离在旋转机械故障集分类中的应用方法[J].振动与冲击，2018，37（11）：48-54.

[9]刘朝阳，陈以，李少博.概率神经网络在手写汉字识别中的应用[J].电子设计工程，2016，24（2）：32-34.

[10]张鹏林，徐旭，杨超，等.基于VMD能量嫡和BP神经网络风电叶片缺陷研究[J].中国测试，2018，44（9）：115-120.

[11]WANG J W，BAI X，YOU X E，et al.Shape matching andclassification using height functions[J].Pattern RecognitionLetters，2012，33（2）：134-143.

[12]ALAJLAN N，RUBE I E，KAMEL M S，et al.Shape retrievalusing triangle-area representation and dynamic spacewarping[J].Pattern Recognition，2007，40（7）：1911-1920.

[13]YANG C Z，WEI H，yi]Q，et al.A novel method for 2dnonrigid partial shape matching[J].Neurocomputing，2018，275（1）：1160-1176.

[14]CHANG C C，LIN C J.LIBSVM：a library for support vectormachines[J].ACM Transactions on Intelligent Systems andTechnology，2011，2（3）：1-27.

[15]刘祥楼，贾东旭，李辉，等.说话人识别中支持向量机核函数参数优化研究[J].科学技术与工程，2010，10（7）：1669-1673.

（编辑：莫婕）