汽车衡秤面防滑纹对称重稳定性的影响研究

赖朝晖　杨晓翔　姚进辉　赖征创

摘要：选取汽车衡秤面周期分布的不同防滑纹类型为研究对象，考虑轮胎的包络特性的条件下分别建立其等效路面高度曲线，研究其对运动车辆的激励作用。建立1/4车辆振动模型，利用轮胎包络特性的半经验方法得到钢板防滑秤面的等效高度曲线，采用轮胎包络特性的面接触模型得到条纹防滑秤面的有效路形，并通过Matlab/Simulink仿真，得出不同类型防滑纹的秤面对车辆激励力的变化曲线。结果表明：对于钢板防滑，当激励频率小于共振频率时，车辆行驶速度越小，产生的激励力越小;当激励频率大于共振频率时，车辆行驶速度越大，产生的激励力越小。钢板间净距小于轮印长度时，间距越小，秤面等效高度曲线波动幅度越小，但接近共振时会引起秤面激励力的增大。对于条纹防滑，条纹与轮胎承载面的接触面积变化越小，变化速率越慢，秤面对车辆的周期激励力就越小。

关键词：轮胎包络特性;称重稳定性;振动分析;防滑纹;货车ETC

中图分类号：TH823;O321 文献标志码：A 文章编号：1674-5124（2019）08-0118-06

收稿日期：2018-08-14;收到修改稿日期：2018-09-07

基金项目：国家重大科学仪器设备开发专项（2011YQ090009）

作者简介：赖朝晖（1989-），男，福建龙岩市人，硕士研究生，专业方向为动态称重系统的开发。

通信作者：杨晓翔（1963-），男，内蒙古赤峰市人，教授，博士生导师，研究方向为计算力学及其工程应用。

0 引言

动态汽车衡计重收费系统现已广泛应用于高速公路收费站，精度较低、防作弊效果差的轴重式动态汽车衡已逐步被称量精度更高的轴组式及整车式动态汽车衡所取代[1]。近几年，我国各省、市、自治区加强ETC车道基础设施建设，ETC模式的货车计重收费与人工半自动化收费方式相比大大提高了货车的放行效率，缓解了车辆的拥堵问题[2]。然而，当前我国ETC车道仅局限于客车，对以计重方式收费的货车尚未实施ETC[3]。现有的动态称重技术（weighing in motion，WIM），车辆计重有两种模式，一种是“一杆一车”计重模式，一种是“整车连续跟车”计重模式;其中，连续跟车计重技术能满足快速称重，快速通行的需要[4]。

连续跟车的动态称重技术，相较于静态称重，还要考虑车辆与秤台之间的动荷载，因而称量的精度远不如静态秤。冯秀丽等[5]对随机路面与汽车动荷载间的关系进行了理论分析与计算机仿真，研究了路面不平度、汽车行驶速度对动态称重结果的影响，为进一步提高汽车衡动态称重的精度提供了理论依据。李斌[6]研究了速度与加速度对动态称重系统的影响，将汽车振动模型进行简化，在给定路况下不同速度的动荷载进行仿真，得到不同速度和加速度对称重精度影响的一般规律。

秤台表面防滑类型主要有周期分布的花纹钢板或防滑条纹两种[7]。不停车收费的计重系统，车辆保持相对较快的速度通过秤台，称重传感器取样时间短，要求相对稳定的称重数据。而秤面防滑纹将对行驶中的车辆产生周期性的干扰力，引起车辆的上下振动。车辆振动产生的低频干扰使传感器的称重数值发生波动，影响称重信号的稳定性，造成电信号采集区间过度分散，进而影响称重精度。本文从不同类型的秤面防滑类型来分析其对行驶车辆的激励响应规律，为秤面防滑的设计和减轻车辆的称重波动提供理论依据。

1 轮胎的滤波效应与等效路面高度

1.1 轮胎的滤波效应

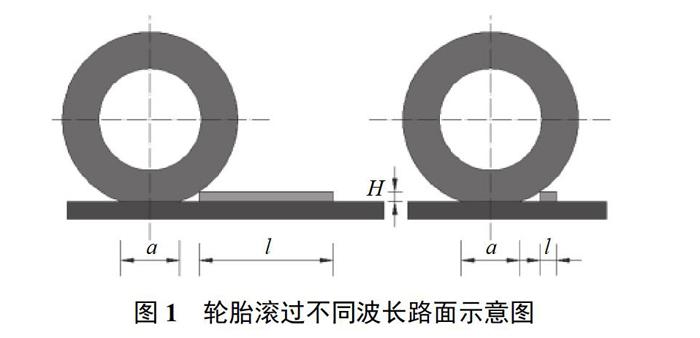
当轮胎遇到波长比接地印痕的长度还长的路面输入时，轮胎可以看作是受到点作用力激励的弹簧阻尼系统;当地面的激勵比接地印痕的长度小时，轮胎表现为包络特性，即轮胎遇到路面的瞬时冲击时，吸收或衰减该冲击的能力，并减小了传递给车辆的能量[8]。如图1所示，当路面凸台波长满足l>a时，轮心将随着轮胎滚动上升的高度为H;而当l

1.2 等效路面高度的建立

因为轮胎的静态垂直刚度随载荷变化很小，可将轮胎在不同位置上的实际静态垂直刚度简化为平路面上的静态垂直刚度，设轮胎轴高不变时，等效路面高度[9]可表示为

式中：F_z——轴高固定时轮心处的垂直力;

F_z0——平路面上轮心处的垂直力;

K_z0——平路面上轮胎静态垂直刚度。

在低速运动下，轮胎的一般特性随运动过程仅有细微变化a由式（1）可知，在给定等效路面高度变化的条件下，可求出运动轮胎轮心所受的垂直力变化。Bandel和Monguzzi[11]提出了一种研究轮胎包络特性的半经验方法，把轮胎在不同路面的响应分解成基本曲线的叠加，如半余弦曲线[12]。

2 焊接防滑钢板周期支承振动

当秤面采用焊接方块防滑钢板时，如图2所示，一般情况下，秤面钢板长度或钢板净间距大于轮印长度，轮胎印痕落在平整秤面上时，等效路面高度等于秤面高度。由于车辆在秤面行驶速度较低，秤面激励频率较低，表现为车身的振动[12]，可用两自由度系统模型。建立具有2个自由度的1/4汽车振动模型[5]，只考虑车身与轮胎的垂直振动，振动模型如图3所示。图中m₂、m₁分别为汽车本身的质量、轮胎和轴的总质量;k₂、c₂分别为汽车悬架刚度及阻尼;k₁、c₁分别为轮胎竖向刚度及阻尼;q为等效路面高度;x₁、x₂分别为轮胎与轴的垂直位移及汽车悬架的垂直位移。

2.1 等幅值的等效路面高度周期激励

车轮滚动越过钢板凸台时，考虑轮胎的包络特性，基本曲线取余弦曲线，取轮胎与凸台接触为曲线起点。如图4所示，设凸台长度为l，凸台净距为s，且满足l>2AB，s>2DE，则等效路面曲线高度的变化幅值与秤面高度变化幅值一致。设车轮水平行驶速度不变，其速度设为v_x，轴重F_G，则轮胎接地印痕半长为

基本曲线半长为a=AB+DE，且有：

令基本曲线为

等效路面曲线为

l+DE-AB≤x

考虑动态汽车衡过秤速度v_x=2m/s，振动参数如表1[5]所示。

设防滑板高度H=4mm，轮胎半径R=635mm，l=0.8m，s=0.5m，根据式（5）可得秤面激励的等效路面高度，如图5所示。

相关参数代入二自由度运动微分方程[5]，可得秤面对轮胎的周期支承激励力变化曲线如图6和图7所示。该振动系统一阶频率1.9HZ，振型[1，2.68]，二阶频率11.9Hz，振型[1，-0.044]。从图6可知，秤面对车辆激励力幅值的最大值与最小值的绝对值并不相等，不同车身质量的振动激励力大小并无明显规律，这是因为车身质量越大，轮胎与地面接触面长度越大，轮胎包络效应越明显。从图7可以看出，当速度为2m/s时，激励频率为1.5Hz，波动荷载约为车辆质量的5.4%;当速度为1m/s时，激励频率为0.8Hz，波动荷载约为车辆质量的3.2%。激励频率小于共振频率1.9Hz时，车辆行驶速度越小，产生的波动荷载越小。在车辆行驶速度为2.47m/s的条件下，激励频率等于共振频率1.9Hz，经计算对比可知波动荷载最大，约为车辆质量的18%。同样，可以验证激励频率大于共振频率1.9Hz时，车辆行驶速度越大，产生的波动荷载越小。

2.2 不等幅值的等效路面高度周期激励

当钢板满足l>2AB，s<2DE，如图8所示，则等效路面曲线应视为基本曲线的叠加，如图9所示，基本曲线非叠加区域如前所述，为使叠加区域满足连续性条件，可设为曲线按如下公式进行叠加：

y=H·（cosα·sin²β+cosβ·sin²α）（6）

叠加后的曲线作为等效路面高度曲线，其最高点与原路面起伏的最高点高度相同，而最低点将高于原路面最低点，将这种曲线称为不等幅值的等效路面高度曲线。

当l=0.8m，s=0.2m时，等效路面高度如图10所示。在表1所示参数下，令v_x=2m/s，秤面对轮胎的周期支承激励力变化曲线如图11和图12所示。从图11可以看出，当l=0.8m，s=0.2m时，秤面对系统的激励频率为2Hz，接近系统一阶频率，振动荷载幅值约为车辆质量的6.4%，显著大于l=1.2m和l=0.5m两种情况。当l=0.8m，s=0.25m时，秤面对系统的激励频率为1.9Hz，引起共振，振动荷载幅值约为车辆质量的8.6%，如图12所示。防滑板间距小于共振间距时，等效路面高度波动幅度减小，振动产生的波动荷载也减小。当钢板间距大于共振时的间距情况下，等效路面高度波动幅度大于共振时的幅度，但是秤面激励荷载并不必然大于共振时的荷载。当间距继续增大时，将满足等幅值等效路面高度的条件，对比图7可知，当s=0.5m时，秤面激励荷载仍小于共振时的激励荷载。

3 焊接防滑条纹周期支承振动

车轮滚动越过微小凸纹时，如图13所示，微小凸纹对轮胎表现为全过程的包络特性，在轮胎的滤波效应下，轮辋竖向运动曲线变化幅度小于相应地面起伏变化幅度。设轮胎滚动过程中，接地印迹长度不变，采用轮胎包络特性的面接触模型[13]，轮胎垂直方向均布刚度为式中：AB——轮胎接地印痕半长;

B——轮胎胎面接地宽度。

设真实路形为q（x，y），则有效路形：

焊接防滑条纹布置形式如图14所示，设条纹高度和宽度均为4mm，轮胎行驶在防滑條纹的中间位置，且轮胎胎面接地宽度B小于条纹宽度b，则在表2所给参数下，有效路形如图巧所示。

将有效路形代入1/4汽车振动模型，得到秤面激励力曲线如图16和图17所示。由图16可知，对于平行防滑条纹，车辆轮胎滚过条纹时，形成瞬时冲击荷载，当速度为2m/s时，波动荷载幅度约为车辆质量的0.32%;当速度为1m/s时，波动荷载幅度约为车辆质量的0.21%。可见车辆行驶速度越大，秤面激励力越大。由图17可知，斜置条纹最大波动荷载约为车辆质量的0.14%，与平行条纹比较，斜置条纹秤面有效路形高度和激励力都较为平缓。与图7相比较可知，焊接防滑条纹对车辆的激励力显著小于焊接防滑钢板。

若防滑条纹布置宽度小于轮胎宽度，即满足b

4 结束语

本研究对动态汽车衡最主要的两种防滑方式分别进行周期支承振动的激励力变化分析，得出的主要结论如下：

1）对于焊接防滑钢板，根据前文中所给的参数的计算结果，当钢板间净距大于轮印长度时，在车辆行驶速度为2.47m/s的条件下，激励频率等于共振频率，波动荷载最大，约为车辆质量的18%。当激励频率小于共振频率时，车辆行驶速度越小，产生的波动荷载越小，如当车辆行驶速度为2m/s时，激励频率为1.5Hz，波动荷载约为车辆质量的5.4%;当速度为1m/s时，激励频率为0.8Hz，波动荷载约为车辆质量的3.2%。同样可以验证当激励频率大于共振频率时，车辆行驶速度越大，产生的波动荷载越小。当钢板间净距小于轮印长度时，间距越小，秤面等效高度曲线波动幅度越小，但接近共振时会引起秤面激励力的增大，共振条件下约为车辆质量的8.6%。

2）对于焊接条纹防滑，车辆轮胎滚过平行条纹时，会形成瞬时冲击荷载，在前文给定的参数条件下，当速度为1m/s时，波动荷载幅度约为车辆质量的0.21%;当速度为2m/s时，波动荷载幅度约为车辆质量的0.32%。可知，激励频率大于一阶共振频率时，速度越大，秤面激励力越大。而斜置条纹秤面有效路形高度变化幅度较小，产生的秤面激励力也较小，最大波动荷载约为车辆质量的0.14%，激励力波动较为平缓。

3）秤面周期分布的防滑纹对车辆产生的波动

（下转第129页）（上接第123页）激励力将造成称重信号的小幅度跳动，影响连续不停车收费系统的称重稳定性，进而影响称重精度。因此，在设计防滑条纹时，应合理考虑条纹的尺寸大小和布置方式，避免对车辆形成共振，如用焊接防滑条纹代替防滑钢板，斜置条纹代替平行条纹，还应尽量减小条纹与轮胎承载面接触面积的变化和变化速率，如适当减小条纹横向布置宽度。此外，在满足秤面防滑性和耐磨性要求的前提下，秤面也可采用涂装防滑涂料，或采用拉毛、压痕或刻痕等防滑处理的混凝土面板结构。

参考文献

[1]朱国伟，范长江，周骥，等.浅谈动态汽车衡发展史[J].中国交通信息化2016（7）：98-99.

[2]张剑勇，周尚儒，杨军.ETC模式货车计重收费系统设计[J].中国测试，2016，42（7）：84-87.

[3]雷茂锦，余绪金，程旻瑞.货车ETC技术的研究与应用[J].中国交通信息化2017（3）：84-86.

[4]孙晓宁.全车型货车ETC技术在河北京张高速公路中的应用[J].中国交通信息化2018（5）：114-115.

[5]冯秀丽，李晓林，杨洪扣.路面不平度与汽车速度对动态汽车衡称重的影响[J].中国科技论文，2012，7（11）：857-861.

[6]李斌.速度与加速度对动态称重系统的影响[J].山西电子技术，2015（1）：43-45.

[7]王同良，冷晓飞，张卫国，等.防滑涂料在汽车衡中的应用[J].中国涂料，2016，31（5）：58-63.

[8]GENT AN，WALTER J D.轮胎理论与技术[M].危银涛，李勇，冯希金，等，译.北京：清华大学出版社，2013：325-327.

[9]郭孔辉，章新杰，吴海东，等.形态学滤波在轮胎包容特性中的应用[J].吉林大学学报（工学版），2009（A1）：1-4.

[10]ALKAN V，KARAMIHAS S，ANLAS G.Experimentalanalysis of tyre-enveloping characteristics at low speed[J].Vehicle System Dynamics，2009，47（5）：575-587.

[11]BANDEL P，MONGUZZI C.Simulation model of thedynamic behavior of a tire running over an obstacle[J].TireScience and Technology，1988，16（2）：62-77.

[12]吳海东.不平路面中频激励轮胎动态特性研究[D].长春：吉林大学，2007.

[13]郭孔辉，刘青，丁国峰.轮胎包容特性分析及其在汽车振动系统建模中的应用[J].汽车工程，1999，21（2）：65-71.

（编辑：莫婕）