基于B样条曲线的轮胎胎面缠绕算法

张 鹏， 沈精虎， 彭 婷

(青岛大学 机电工程学院，山东 青岛 266071)

0 引 言

轮胎胎面成型是工程机械轮胎、农业轮胎、巨型工程轮胎等轮胎生产领域中最生产的重要环节之一[1]，轮胎胎面缠绕的质量对轮胎生产领域有着至关重要的作用。随着国际轮胎产业竞争日趋激烈，轮胎生产企业对于产品提出了新的质量控制要求，对轮胎缠绕过程的精度有了更高的需求[2]。针对这一需求，轮胎胎面缠绕的技术改造成为解决问题的关键，对此，需要开发具有更高精度的轮胎胎面缠绕算法，提高缠绕胎面质量和胶条分布的稳定性与准确性，降低研发成本和废品率。

目前国内外工程机械轮胎胎面缠绕生产线中，主要结构方式有以下缺点：一是对于轮胎胎面基线，主要采用像素法[3]等仿形原理[4～6]，大多数轮胎产业对于轮胎截面的数学描述仅限于直线与圆弧等简单的几何线条[7]，对轮胎基准面的数学描述产生误差；二是胶条缠绕过程中无法做到对缠绕的每一根胶条的形状位置进行精确地控制，缠绕结束后的轮胎胎面与工业需求的理想胎面有一定差别，此时往往需要工人的操作进行干预使得成品更加接近理想胎面，具有较高的废品率。

基于以上因素，为了能够精确描述轮胎胎面的缠绕过程，本实验利用简单实用并且具有良好低阶光滑特性的B样条曲线[8]来描述轮胎胎面与胶条形状位置的变化，对于轮胎胎面基线上已知的型值点坐标，使用B样条曲线反求控制点的方法得到精确的轮胎胎面基线。同理，每根胶条缠绕的具体过程也用B样条曲线来进行高度精确地仿真，通过对缠绕过程中每根胶条形状位置的精确控制得到更精确的轮胎胎面缠绕过程。

1 胎面成型原理与所需参数

工程胎面的缠绕成型实际上是两种运动复合的结果，如图1所示具有一定断面形状的胶条，由缠绕机缠绕到胎胚上，在缠绕鼓绕X轴转动的同时,缠绕机沿X轴缓慢平移,则胶条将有规律地贴合成型[9]。若要精确描述轮胎胎面缠绕过程，轮胎缠绕机工作时需要以下几个目标参数：

1)对于胶条缠绕机，需要随时间变化的轮胎缠绕机机头的空间坐标P(x,y,z)以及所对应的缠绕机头倾斜角度θ。

2)对于胎胚，由于缠绕过程中，胶条的进给速度与轮胎自转的线速度保持一致且恒定，而胶条在同一位置的多次缠绕会导致轮胎的半径增大[10]，故需要缠绕过程中轮胎自转的角速度w随时间变化的函数曲线。

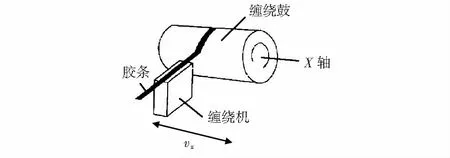
图1 缠绕原理示意

轮胎缠绕前，本实验所采用的轮胎工艺参数如表1所示，胎面缠绕所需尺寸如图2所示，具体为(0,-225),(15,-195),(28,-150),(34,-120),(36,-90),(34,-45),(22,-15),(22,0),(22,15),(34,45),(36,90),(34,120),(28,150),(15,195),(0,225)。

表1 轮胎工艺参数

图2 胎面缠绕尺寸

2 基本原理

胎面缠绕前，需要以轮胎胎体基准面与缠绕后理想轮胎胎面为基准进行缠绕。

2.1 绘制轮胎基线

本实验基于准均匀三次B样条曲线[11]，根据以往工艺专家人工诊断的经验，在轮胎截面的基线上取15个重要的型值点，根据已知的型值点坐标通过准均匀三次B样条反求控制点的方法得到轮胎胎面基线的控制点坐标，三次准均匀B样条反求控制点矩阵方程如下

(1)

式中Q为控制点，P为型值点。

得到控制点坐标后，即可根据准均匀三次B样条曲线理论得到轮胎基线的参数化方程，根据方程即可绘制轮胎基线，实现对轮胎基准面曲线的精确数学描述。三次B样条参数曲线方程的第i段为

(2)

2.2 绘制缠绕后理想胎面曲线

若曲线上某点A坐标(x,y)已知，该点对应的法线斜率k与法线方向上的距离h已知，可以求得另一点B的坐标。由图2胎面缠绕尺寸与轮胎基线参数方程，可以通过上述方法求得缠绕后理想胎面曲线上的型值点坐标，从而求得缠绕后理想胎面曲线曲线方程。

如图3所示，根据上述方法，对轮胎基线上的型值点A可以求出2个符合条件的点B1与B2，但根据实际情况胶条必定缠绕在轮胎基线上方，故只有点B1符合要求，此时可以通过比较轮胎中心点O1与两点之间的距离O1B1,O1B2的长度，来排除点B2造成的干扰。根据上述方法，得到所需的缠绕后理想胎面的型值点坐标后，再次通过三次准均匀B样条反求控制点，得到所需的缠绕后理想胎面曲线方程，绘制缠绕后理想胎面曲线见图3。

图3 轮胎外廓曲线示意

3 胶条缠绕过程

如图2，本实验中轮胎缠绕机所使用的胶条断面形状为梯形，其下底宽75 mm，上底宽45 mm，胶条厚度为3 mm。

3.1 分 层

以轮胎基线与缠绕后理想胎面曲线为基准，由于两条曲线之间胶条缠绕厚度可能较大，会导致胶条缠绕时倾斜角度过大造成缠绕不稳定的情况，需要在胶条进行缠绕前，对胶条是否分层进行判断。以图2胶条缠绕尺寸为例，根据胶条缠绕后厚度的最高点最低点以及胶条的型号为判断标准，将缠绕过程分为两层，分层曲线见图3。

3.2 定位第一根胶条位置

确定分层后，将分层曲线设置为缠绕结束后的理想曲线，假设轮胎缠绕方向为从左到右。以胶条下底为基准，将梯形的胶条划分为n份(根据实际经验使用不同的划分方法，本实验采用的划分方法为每隔5 mm将每根胶条均匀竖直划分为15份)。

胶条开始缠绕，将胶条下底左端点与轮胎基线左端点重合，胶条的下底曲线沿着轮胎基线从左到右贴合，根据胶条下底不同型值点之间的曲线长度以及轮胎基线参数方程得到位于胶条下底的16个型值点坐标，从而求得拟合在轮胎基线上的第一根胶条下底的曲线方程(理论上在定义域内，第一根胶条的曲线方程与轮胎基线方程一致)。

根据胶条下底型值点所对应的法线斜率以及不同位置胶条断面的厚度，求得胶条上底的曲线方程，从而得到第一根胶条在轮胎胎面缠绕过程中的精确位置。

3.3 定位后续胶条位置

由于胶条的上底曲线和分层曲线一定会有交点存在，联立胶条的上底曲线和分层曲线的参数方程求得交点坐标P，以该点坐标作为下一根即将缠绕的胶条下底左端点，使得下一根胶条贴合在上一根胶条的上底以及轮胎基线上，如图4所示，P1,P2为两根不同胶条的上底曲线与理想曲线的交点。

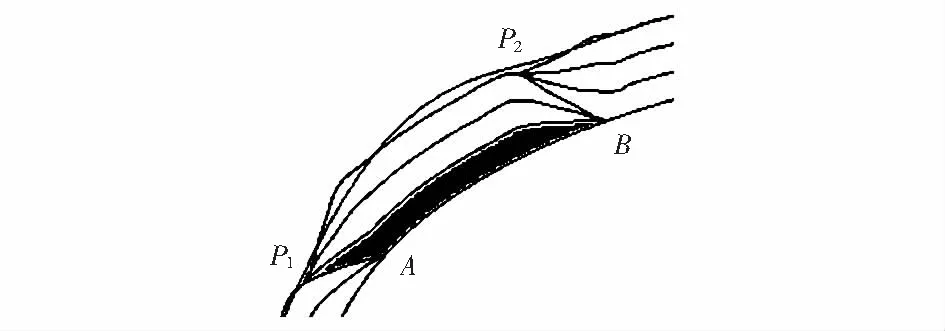
图4 胶条搭接示意

图4中，以阴影部分胶条为例，胶条下底的16个型值点分布在曲线P1A与AB两部分上，根据胶条下底不同型值点之间的曲线长度与两条曲线P1A,AB的参数方程可以求得下底型值点的坐标，进而求得胶条上下底的曲线方程，从而得到阴影部分胶条的具体位置。

3.4 终止条件

使用上述方法进行缠绕，当计算出下底型值点坐标中出现点的横坐标超过轮胎基线上的最大横坐标值，即胶条缠绕至右侧边界时停止缠绕，视为该层缠绕完成。

3.5 后续分层缠绕

胶条缠绕需要分层时，则从第一根胶条起始点缠绕开始，每一根胶条上底和分层曲线的交点之间的曲线，如图4中曲线P1P2。将曲线P1P2之间的所有上底型值点坐标进行记录保存，在第一层缠绕结束后，将所有记录的型值点通过准均匀三次B样条反求控制点的方法，求得实际缠绕后的分层曲线方程。以该方程与最终的理想胎面方程为基准重复上述步骤，即可完成轮胎胎面全部缠绕过程。

3.6 结果分析

在本实验中，每一根胶条缠绕时，轮胎缠绕机机头的空间坐标P(x,y,z)以及所对应的缠绕机头倾斜角度θ皆可通过胶条的上下底参数曲线方程进行极为准确的描述。每根胶条缠绕对应的轮胎自转角速度ω可由胶条的进给速度与每根胶条对应的不同的轮胎半径求得。

3.7 误差处理

1)如图4所示，曲线P1P2有超出分层曲线的部分，此时可以将交点P1进行沿着曲线P1A向右移动，直至超出部分的面积误差达到接受范围内时，再以新的P1点作为下一根胶条的左端点进行后续缠绕。

2)本文采用的胶条缠绕方式，如图5所示，从实际胶条贴合的局部放大图可以看到，这种理论计算结果实际并不会完全做到，计算曲线长度时使用的是曲线CA段与AB段，而胶条的实际位置是虚线的CB段，由此会产生空隙，造成误差。

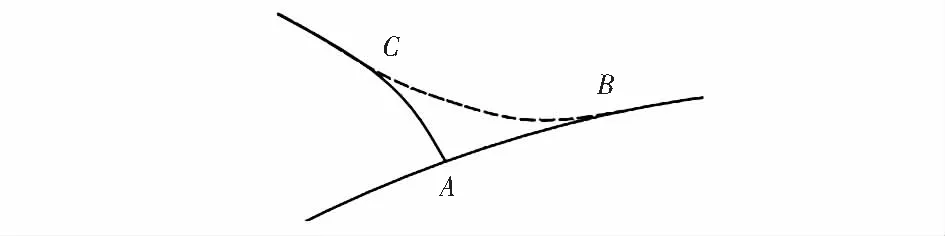
图5 实际胶条贴合的局部放大

可以通过采取曲线细分方法[12]来减小误差。所谓曲线细分方法，就是在曲线长度不变的情况下，增加曲线上型值点的个数，即胶条下底的型值点个数，将空隙尽可能的减小，将误差值控制在接受范围内。

4 实例分析

采用上述算法，基于Windows 10操作系统，利用Visual Studio 2017与针对C++的EasyX图形库，为工艺人员提供了自动生成某种型号轮胎缠绕过程的仿真系统。在数据库中提取轮胎工艺参数，工艺专家只需要选取重要的型值点坐标以及所需胶条断面形状，即可得到轮胎缠绕仿真截面图，如图6所示。

图6 缠绕一层轮胎截面

5 结 论

与像素法扫描轮胎曲线相比，通过B样条曲线来模拟仿真轮胎胎面缠绕，对每一根胶条的形状位置都能够精确控制；与直线圆弧等简单曲线相比，样条曲线精准度更高,对胶条位置的定位误差缩小到0.1 mm以内。通过工艺人员给定轮胎工艺参数与胶条型号，即可通过该算法得到基于B样条曲线的精确轮胎胎面缠绕过程，使轮胎生产工艺的准确性和效率得到了极大提高，并且降低了设备上的生产成本，有效降低废品率，对轮胎缠绕技术发展具有极大的实际意义。