基于参数融合机器人旋转关节轴鲁棒性控制律

张亚婉，陆兴华，吴宏裕

(广东工业大学华立学院，广东 广州 511325)

0 引 言

机器人旋转关节轴是机器人进行抓取、攀爬以及行走等作业的重要部件，该部件的稳定控制是保障机器人稳定可靠性运行的关键。对机器人旋转关节轴的准确、可靠控制是建立在对关节的准确定位和测姿基础上的。结合对运动参数的融合处理，提高对移动机器人旋转关键轴的可靠控制能力，最终将控制律嵌入到机器人的惯性导航系统(inertia navigation system，INS)中[1]，提高机器人的动态稳定控制能力，研究机器人的稳定控制律，在机器人的控制设计中具有很好的应用价值。

传统方法中，对机器人旋转关节轴的内控制方法主要有PID控制方法、反演积分控制方法以及卡尔曼滤波控制方法等。无论哪种方法，都需要对机器人的旋转关节轴进行绝对角度解算，得到姿态角，结合惯性参量融合，进行机器人的鲁棒性控制。Marins等提出了一种四元素的扩展卡尔曼滤波方法(EKF)[2]，采用三轴坐标系模型构造机器人旋转关节轴的运动学方程，使用欧拉角计算姿态角，从而消除了姿态估计误差，但该方法的计算开销较大，对机器人控制的实时性不好[3-4]。文献[5]中提出一种基于机器人姿态跟踪的旋转关节轴控制方法，融合扩展卡尔曼滤波和无迹卡尔曼滤波(UKF)，提高姿态估计和控制参数的融合能力，但该方法进行机器人控制的鲁棒性较差，抗扰动性不好。

针对上述方法存在的问题，文中提出一种基于运动参数融合的机器人旋转关节轴鲁棒性控制律。构建机器人旋转关节轴的动力学模型，采用姿态传感器进行机器人旋转关节轴的运动姿态参数采集，对采集的姿态参数采用Kalman滤波算法进行误差补偿和信息融合处理，根据运动参数的融合结果采用模糊控制方法进行机器人旋转关节轴控制律设计。最后进行仿真实验分析，验证该方法在提高机器人旋转关节轴鲁棒性控制能力方面的优越性能。

1 被控对象描述和参量分析

1.1 机器人旋转关节轴的动力学模型

为了实现机器人旋转关节轴鲁棒性控制优化，首先构建机器人旋转关节轴的动力学模型，采用姿态传感器进行机器人旋转关节轴的运动姿态参数采集[6]，构建机器人旋转关节轴的无阻尼自由振动系统方程：

(1)

假设机器人旋转关节轴的末端位姿运动是一个纵向的线性运动模型，根据阻尼力矩与末端位姿协同控制的关联关系，得到位姿修正的反馈最小信息熵泛函数学模型：

(2)

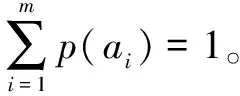
(3)

δ·p1-2p2+ρ2A2-δρ1A1+c2+cr=0

(4)

ρ2(p2-c2-cr)-δ·(1-δ)μ2A2=0

(5)

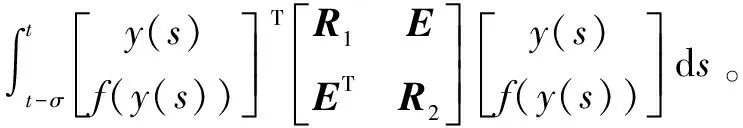
1.2 机器人旋转关节轴的运动姿态参数分析

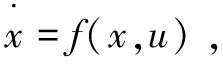
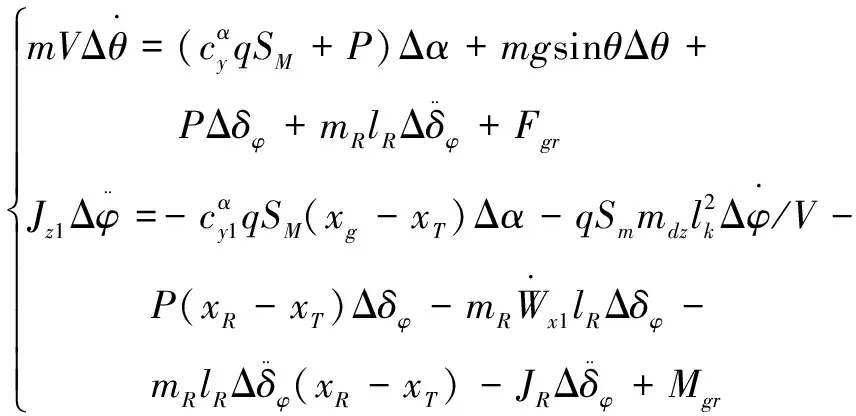
(6)

根据磁力计对旋转关节轴的采集结果进行信息融合，用Ψ2(d2(t))表示矩阵L(Z2+Z3)-1LT与MT(Z2+Z3)-1MT的Bergmann核[8]，由此判定机器人的旋转关节轴控制系统是否稳定，判决方程为：

(7)

采用滑膜积分控制方法进行机器人旋转关节轴运动的稳态控制，构建机器人旋转关节轴运动姿态稳定控制的数学模型和动力学模型[9]，得到机器人旋转关节轴助力转向系统的动能T和势能V：

(8)

V=MPgLcosθP

(9)

对采集的姿态参数采用Kalman滤波算法进行误差补偿和信息融合处理[10]，得到机器人旋转关节轴控制的平衡解满足：

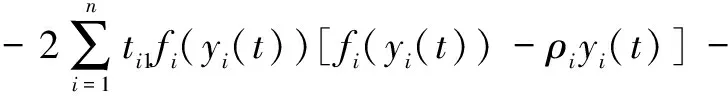
ρiyi(t-δ(t))]=-2fT(y(t))T1f(y(t))-

2fT(y(t-δ(t)))T2f(y(t-δ(t)))+

2yT(t)ΣT1f(y(t))+2yT(t-δ(t))ΣT2f(y

(t-δ(t)))

(10)

结合约束条件，可以得到机器人旋转关节轴运动控制的稳态条件[11]。

2 控制律的优化设计

2.1 运动参数的Kalman滤波融合算法

在构建机器人旋转关节轴的动力学模型，采用姿态传感器进行机器人旋转关节轴的运动姿态参数分析的基础上，进行机器人旋转关节轴控制律的优化设计。文中提出一种基于运动参数融合的机器人旋转关节轴鲁棒性控制律。机器人旋转关节轴的运动姿态调节的概率分布项为{p(x1),p(x2),…,p(xm)}。机器人旋转关节轴在7自由度空间内进行稳态调节，在控制约束方程的两端同时除以pqrsdp，得到：

(11)

构建机器人旋转关节轴问题控制的微分方程代数方程组：

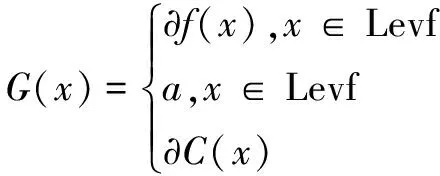
(12)

其中，稳定性平衡点满足：

(13)

采用Kalman滤波算法进行误差补偿和信息融合处理[12]，Kalman滤波传递函数为：

(14)

(15)

误差补偿和信息融合处理后机器人稳态控制的稳定性参数模型满足：

(16)

当([pHj,pLj])⊆([pHi,pLi])时，表示命题Aj支持Ai，即Aj⊂Ai，由此得到了机器人旋转关节轴控制的周期解稳定性约束条件[13]。

2.2 机器人鲁棒性控制律

根据运动参数的融合结果采用模糊控制方法进行机器人旋转关节轴控制律设计，采用非交换微分调控方程[14]，得到机器人旋转关节轴鲁棒性控制的边值周期解向量的分配函数为：

(17)

当双边界条件下，若矩阵A满足A=AH,其中AH=(A*)T,“*”代表求共轭，引入误差反馈调节，得到机器人旋转关节轴避障控制参量调节的控制修正分配函数。机器人旋转关节轴的位姿平衡点位于平面坐标系象限时，即(x1,x2≥0)才有实际意义。由Schwartz不等式可知|ρik|≤1，那么对机器人旋转关节问题控制的边值周期解的插值拟合式为：

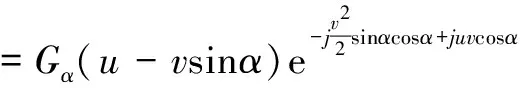
(18)

采用模糊控制方法进行机器人旋转关节轴控制律设计，模糊控制函数m(A)满足：

(19)

(20)

令A∈Cn×n(n×n维复数空间)，采用运动参数融合方法，得到机器人旋转关节轴鲁棒控制的最优解分别为：

(22)

将机器人的鲁棒控制周期解问题转换为求超定方程的最优解问题[15]，收敛性评价规则如下:

Ni,j= (f(A)i,1⊗f(B)1,j)⊕(f(A)i,2⊗f(B)2,j)⊕…⊕(f(A)i,h⊗f(B)h,j)=

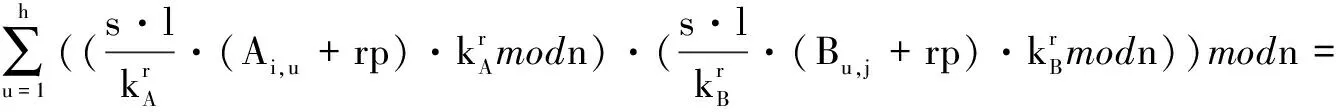
rp+r2p2)modn

(23)

根据稳定性判决条件，得到文中设计的机器人旋转关节轴抗扰动鲁棒控制律是渐进稳定的。

3 仿真实验与结果分析

通过仿真测试文中方法在提高机器人旋转关节轴控制中的应用性能。采用AD公司出品的MSP430系列超低功耗16位信号传感器进行机器人旋转关节轴信息采集，设定PLL_LOCKCNT寄存器，OUTD管脚输出电压为0～15 V，对机器人的运动参数采集的初始频率为100 Hz，截止频率为300 Hz，在小扰动信噪比(SNR)分别为-5 dB、5 dB、20 dB的条件下，得到姿态参数融合结果，如图1所示。

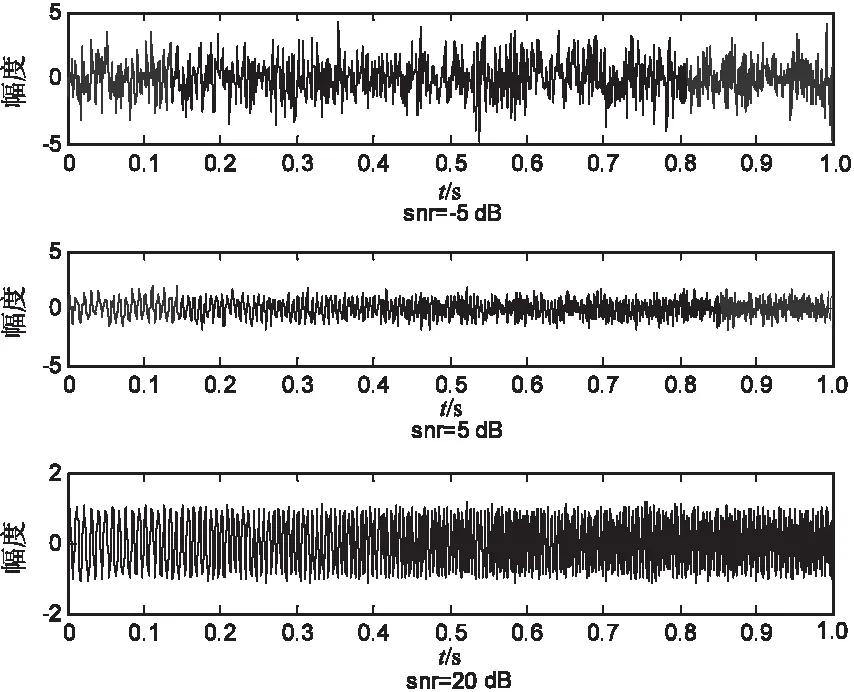
图1 机器人的运动参数采样结果

对采集的姿态参数采用Kalman滤波算法进行误差补偿和信息融合处理，根据运动参数的融合结果进行机器人旋转关节轴鲁棒性控制，得到控制参数融合结果输出，如图2所示。

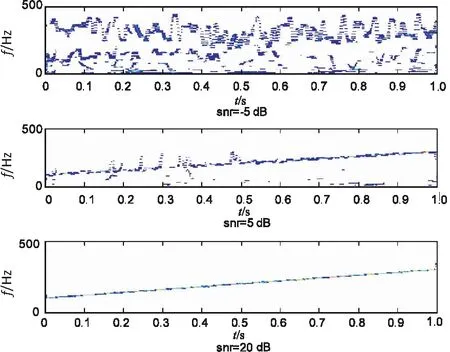
图2 机器人旋转关节轴的参数融合输出

分析图2得知，采用文中方法进行机器人旋转关节轴控制的鲁棒性较好。测试不同方法进行控制的精度，得到的对比结果如图3所示。分析图3得知，该方法进行机器人旋转关节轴控制的精度较高，抗扰动能力较强。

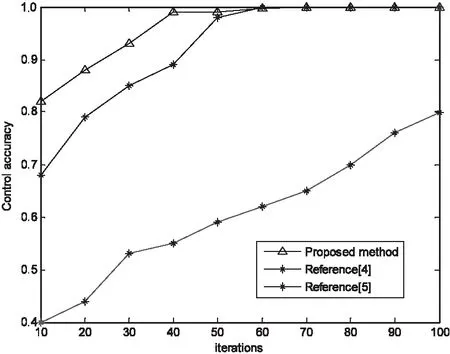
图3 控制精度对比

4 结束语

对机器人旋转关节轴的准确、可靠控制是建立在对关节的准确定位和测姿基础上的，结合对运动参数的融合处理，提高对移动机器人旋转关键轴的可靠控制能力。文中提出一种基于运动参数融合的机器人旋转关节轴鲁棒性控制律。构建机器人旋转关节轴的动力学模型，采用姿态传感器进行机器人旋转关节轴的运动姿态参数采集，对采集的姿态参数采用Kalman滤波算法进行误差补偿和信息融合处理，根据运动参数的融合结果采用模糊控制方法进行机器人旋转关节轴控制律设计。

仿真结果表明，利用该方法进行机器人旋转关节轴控制的鲁棒性较好、精度较高。