基于跨模态检索的效率优化算法

徐明亮，余肖生

(三峡大学 计算机与信息学院，湖北 宜昌 443002)

0 引 言

随着互联网技术的不断发展变化，人们越来越注重于信息的交互。人们对于信息的需求已从最初的单一新闻上的文字发展到后来的图片、视频、声音等。在各种网络平台上，这些不同类型的数据相互交织，互为补充，且存在一定的关联。同一信息可能以不同类型的数据呈现。为了从不同类型的数据中同时找到表示同一信息的数据，跨模态信息检索技术应运而生。

传统的信息检索主要针对同类型的数据提取特征向量，对其进行相似度度量，根据相似度的排名来实现单模态的信息检索。而跨模态信息检索则是建立不同模态的隐式关系模型，让不同模态能在同一空间下像单模态度量一样进行相似度度量，从而完成不同模态间的相互检索。不同类型的模态数据，由于提取的特征向量的方式不同，导致在同一空间投影和匹配时工作量巨大。针对传统的跨模态检索算法在处理高维度计算量巨大的问题，文中提出了一种跨模态信息检索的优化方法。实验表明与原有算法相比，该方法在保证查准率基本不变的情况下，可以大幅减少原有算法的计算量，提高检索效率。

1 相关研究

跨模态信息检索主要包括三个步骤：一是提取不同模态的特征信息来构建特征子空间；二是采用某种算法判断不同模态间特征子空间数据的关联性；三是在特征子空间下进行相似度度量，得出相应结果。

1.1 模态信息特征表达

为了提取不同类型数据信息，需对原始数据进行特征提取，取出原有数据特征向量。根据图像的特征表示，图像类型的特征可分为全局特征和局部特征两大类。对全局特征而言，常用的提取结果主要有颜色直方图和纹理灰度矩阵；对局部特征，常用的处理结果主要有尺度不变特征，方向梯度直方图等。对文字类型的特征表达，常用的有词袋模型(BOW)，通过计算词在文章出现的频率来比较不同文档的相似度[1-2]。另有学者提出了一些基于词袋模型的特征提取算法[3-4]，如潜在语义分析(LSA)、概率潜在语义分析(PLSA)以及隐含狄利克雷分布(LDA)。这些算法能在一定程度上将多媒体同构信息的特征内涵信息表示出来。

1.2 异构特征关联

要解决不同模态数据之间的相关性，关键是构造一个公共的特征子空间，将不同模态的数据特征向量映射到该空间中，然后在该空间上对不同模态的数据进行相似度度量。一般有两种构建公共子空间的模式，一种是基于相关性的特征子空间投影(CM)，该模式下遵循最大相关性原则，一般使用相关性算法找出相对应的投影子空间矩阵，通过子空间投影矩阵来挖掘不同模态间的潜在关系；一种是基于高层语义的特征子空间学习(SM)，这种模式是通过机器学习的方式，使用分类算法在语义层次上对异构数据构建同型语义特征空间，再在该空间下进行相似度处理。此模式通常需要事先安排好分类学习参数，若语义维度发生变化则需要重新调整参数和分类模型，难以进行实际检索应用。因此，文中只探讨第一种基于相关性子空间投影的模式的优化算法。其中这两种方式经常使用的是典型相关性分析法(CCA)[5-7]。

为了探究不同变量组间的相关关系，传统的典型性相关法的基本思路是将变量组间的每一组变量进行线性组合，得到新的典型变量，找到该线性组合中具有最大相关性的一组作为典型变量进行处理。如：有两组变量x=[x1,x2,…,xm]，y=[y1,y2,…,yn]，将其中每一组变量进行线性组合：

此外，为了解决原有数据非线性、非正交的问题，有学者提出了处理非线性的核化典型相关性分析(KCCA)[12]、混合概率相关性分析(mixPCCA)[13]、深度典型相关性分析(DCCA)[14]等方法。

1.3 空间信息相关性检索

根据在同一特征子空间的投影，用投影之间的相似度来度量查询信息与被检索信息之间的相关性，根据相关度的大小来判断与查询信息最匹配的相关信息[15]。一般相似度采用的度量距离有欧氏距离、余弦距离、L1范式距离等。

2 基于降维的跨模态信息检索模型

针对传统算法在进行高维度计算时计算量过大的问题，提出一种新的跨模态相似度学习方法，对传统的基于特征子空间关联算法进行改进优化，以减少原有算法的计算量，提高算法效率。

2.1 模型构建

假设数据存在两种类型X和Z，其特征向量分别为X={x1,x2,…,xn}∈RDx×n和Z={z1,z2,…,zm}∈RDz×m，存在一个跨模态数据集O，使其中每个数据由这两种模态组成。为简单起见，假设每个数据仅包括两个单数据类型，即oi={xi,zi}[16]。

2.2 相关性分析改进及投影子空间

传统的特征子空间投影技术是指先将不同类型数据的特征空间正交化联系在一起，然后挖掘异构数据特征之间的内在关系，找出能将异构数据投影到同一特征子空间内的方法。相关性子空间投影技术则是设法学习找到最优子空间投影矩阵，从而实现将异构数据特征转换到同形特征空间，并保留最大关联性。在这一子空间上可对投影数据进行直接的相似度度量处理。这一过程是对原有特征直接进行投影。而文中优化算法则是先利用主成分分析法将原共生矩阵进行降维，将其矩阵O先进行中心化。中心化是指先计算每个维度平均值，再把每个维度的特征值都减去该均值。之后再计算中心化样本矩阵的协方差矩阵，计算其协方差矩阵的特征值和特征向量(假设求出的特征值共有20个，选定一个合适的特征值最大区间，比如前90%，即前18个最大特征值对应的特征向量)，得到对应矩阵U，再根据降维转换公式J=OU，就得到转换后的降维矩阵J。与原矩阵相比，降维后的矩阵处理速度大大提高，虽然可能有信息损失，但可以接受。

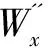
2.3 相似度度量

投影后的矩阵就可以对其进行距离度量，常用的有L1范数、欧氏距离、KL距离、余弦距离等。

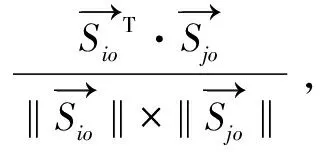
最后为度量查询数据与被查询数据之间的关联性，要对相似度大小进行排序。具体是统计每一组查询数据与被查询数据之间相似度距离，根据相似度距离进行排序，找到相似度最高的作为检索结果展示。

3 实验结果及分析

3.1 实验数据和流程

实验选取文本、图像作为跨模态信息检索的数据，以“文本搜图像”和“图像搜文本”作为实验任务。选取的数据集是Wikipedia跨模态信息检索数据集，包含两千多份文档和10个主题。

特征提取部分：对文本数据，利用gensim工具包提取主题空间的特征，构建特征空间W，维度为10。对图像数据，利用VLFeat机器视觉库计算出其在BOVW图像空间上的特征，构建特征空间G，维度为128。

对特征子空间投影，将得到的图像特征X和文本特征Y先进行中心化处理，再将处理后的数据进行主成分分析，选取一个合适的提取量，得到降维后的图像和文本特征向量，再对降维后的数据进行典型性分析，得到相应文本和图像的投影函数XCCA和YCCA。再分别与降维后的图像文本特征相乘，得到相应投影在公共子空间的图像文本向量。最后根据相似度进行度量，可分别运用KL距离，第一、第二范式，归一化相关性(NC)和归一化交叉相关性度量(NCC)来进行度量。文中主要选取NC与NCC进行度量。为方便起见，选取主成分分析的特征值比例为前95%和90%。

3.2 实验结果对比

为方便计算，选定子空间的维度为6维、8维，相似度度量选取归一化相关性NC，然后比较不同方法之间的区别。计算结果分别如表1和表2所示，将时间分别进行统计比较后，结果如图1～图3所示。

表1 维度为6时的计算结果

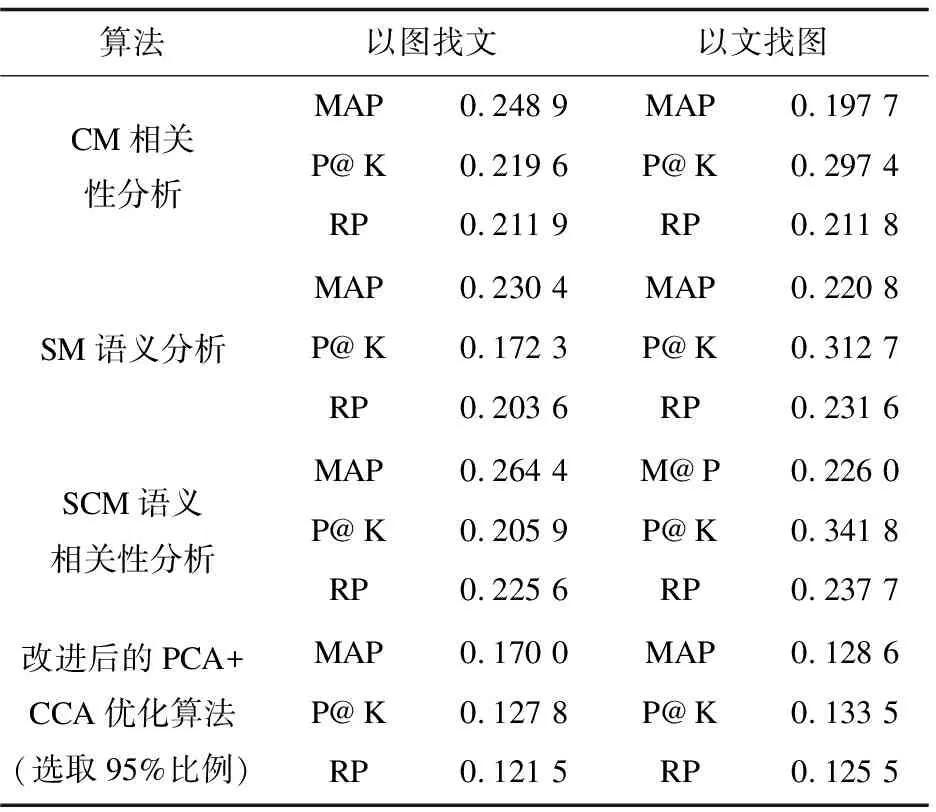
表2 维度为8的计算结果

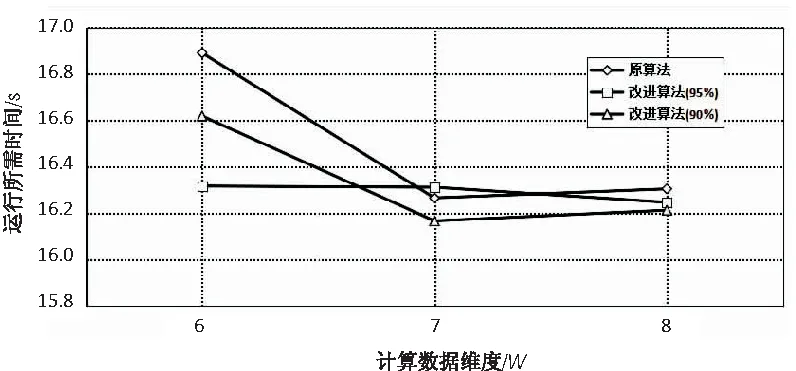
图1 总时间统计

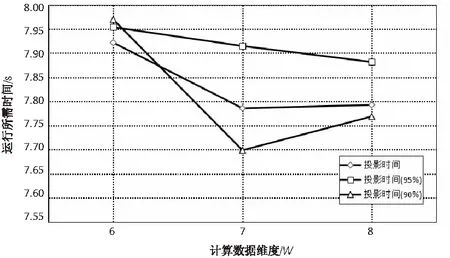
图2 相应的投影时间比较

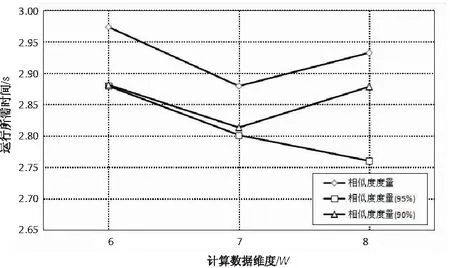
图3 相似度计算时间度量

从图中可看出，改进后的算法所需时间明显低于传统算法的计算时间。总体优化比例平均为1-(16.3/16.9)=3%。由于实验源数据量不大，在进行数据样本预处理时，实验所做的是对样本整体都进行主成分分析，而在之后的检索比较过程中只是选取部分样本进行了检索，因此在总体时间上优化效率不是特别明显。但该优化算法的优势在于，在进行后续向量投影和相似度度量方面，使用时间明显比传统算法要少。所以，在进行跨模态信息检索时，如果数据源数据越大，相比传统算法，此优化算法检索结果的时间越少。

4 结束语

针对传统跨模态检索算法存在处理高维度计算量巨大的问题，提出的算法在向量投影和相似度度量方面进行了改进并进行了实验验证。实验结果表明，该算法明显提高了跨模态信息检索的效率，在大数据量的情况使用，效率可以提高到6%左右。同时在处理更大数据的情况下，该算法在检索时间上有更大优势。

算法的不足之处在于在处理数据时，没有解决数据非线性非正交的问题。在处理主成分比例时，选取的比例不是相对最好的，需要人工选取比例。之后的工作将对这些不足之处进行研究。