基于稀疏子空间的卷积神经网络目标跟踪
李福进 李军 宫海洋


摘要:针对粒子滤波目标跟踪过程中初始化和权值退化的数据处理情况,在粒子滤波框架下提出一种基于稀疏子空间的卷积神经网络目标跟踪算法。以仿生学为基础,在目标跟踪过程中引入稀疏子空间和卷积神经网络。首先,利用稀疏子空间模型筛选出与目标状态相似度较高的候选区域进行后续跟踪处理,减少冗余计算并降低跟踪的复杂性;然后,将稀疏子空间输出用作卷积神经网络的输入,并利用卷积神经网络模型对图像数据处理的优点进行目标跟踪的数据处理;最后,通过对目标数据的不断更新来减少目标表观变化的影响。实验表明,该算法能够更好地处理目标跟踪中的目标遮挡、运动模糊、光流与尺度变化,提高算法的准确性和数据处理能力。
关键词:稀疏子空间;卷积神经网络;粒子滤波;目标跟踪;相异系数矩阵
中图分类号:TP18 文献标志码:A 文章编号:1674-5124(2019)07-0122-06
收稿日期:2018-05-16;收到修改稿日期:2018-07-08
基金项目:国家自然科学基金(61203343);河北省自然科学基金(E2014209106);河北省高等学校科学技术研究青年基金项目(QN2016102,QN2016105)
作者简介:李福进(1957-),男,河北唐山市人,教授,硕士生导师,博士,主要研究方向是智能控制与智能仪表。
0 引言
目标跟踪是用来估计视频中所标记的目标状态过程。以图像处理技术为核心,在计算机视觉领域中目标检测、目标跟踪、目标识别、三维重建、姿态估计等一直是非常热门的研究方向。2013年,Wang等[1-2]针对目标跟踪准确性问题提出LDSs算法,通过聚类和噪音压制的一系列方法,在UCF体育和电影数据方面有很大提高。2014年,张才千等[3]提出了基于目标跟踪的粒子群粒子滤波算法,通过粒子群实现粒子优化使大部分粒子移动到密集分布区域,通过实验验证了粒子的滤波能力有明显提高。2014年,许伦辉等[4]提出一种改进粒子滤波对人物跟踪的应用,在粒子滤波的基础上提出融合权值繁衍和遗传算法相结合,使得算法以相对少的计算量得到更高的准确度,较好地解决粒子滤波算法中初始化与重采样过程带来的误差问题。2015年,许婉君等[5]提出显著性模型和稀疏编码结合来检测遥感图像,将特征矩阵作为训练对象来形成模型,并构建GBVS,SR,SDS,FT,WSCR顯著图。当前比较流行的LRSP算法[6]在2016年由陈芸等提出,改进了传统算法,提高对大尺度目标进行跟踪的准确性。
针对目标跟踪的鲁棒性和准确性,本文提出一种基于稀疏子空间的卷积神经网络目标跟踪算法研究,仿照人眼视觉神经系统[7],能快速有效地定位重要的目标并进行分析,通过聚类映射数据并学习分类器,粒子滤波用于实现在线跟踪目标。在实验环节,将本文所提出的跟踪算法与相关的跟踪算法的跟踪性能对比,通过定量和定性分析,验证算法的有效性。
1 粒子的稀疏子空间表示
人类视觉的认知能力非常强,其注意机制可以在恶劣的环境下准确识别和跟踪目标。人类视觉系统研究的主要目的是让计算机模拟人的思维活动以优化算法提高精度与效率,在复杂环境中做出一定的决策。有研究[8-9]表明,人类视觉被某个物体所吸引时,只有少量的神经元被激活,大多数神经元则处于睡眠状态。这表明当观察目标时,可用少量的神经元来对目标进行表示。稀疏表示受人类视觉系统的工作特点启发,是信号处理领域的热点之一,广泛应用于模式识别[10-11]。
稀疏即是将高维空间数据映射到低维空间中,已知源数据X={x1,x2,…,xM}和目标数据Y={y1,y2,…,yN),利用度量标准计算源数据与目标数据之间的相似性。假设D为一相异矩阵,D=[d1,d2,…,dM]T,D里的每个列向量均为相异系数矩阵,即:式中M、N分别为源数据和目标数据中元素的个数;di,j示xi与yj相似程度,用欧氏距离计算,di,j值越小说明相似程度越高,在实际中的跟踪效果越好。稀疏子空间建模为:假设存在一个概率矩阵Z∈RM×NZ中的元素zi,j与元素di,j一一对应,用相异性矩阵D求解概率矩阵Z,通过以下优化问题求解:式中‖.‖p表示‖l‖p范数;I(t)表示指示函数,当t=0时,函数值为0,否则值为1;λ>0,为平衡前两项约束的参数;ωj>0,是惩罚因子;ej∈[0,1],表示yj是奇异元素的概率。公式(2)可以通过乘数交替方向算法求解。当源数据中的xi对应的系数矢量zi满足max(zi)>μ‖zi‖1,则xi为子集合中的元素,文中μ取值为0.2。目标数据Y中yj可以用子集合中的元素稀疏表示:
δyj=argmaxzi,j,i∈{l1,…,lC}(3)式中δyj∈[1,…K]表示目标数据Y中yj的类别,K为聚类中心数量;C为子集合中元素的数量。子集合的类别定义为系数矢量的最大值所对应的目标数据的类别。通过式(2)和式(3)可将候选区域聚类同时将目标数据分配类别,使得后续处理中冗余计算降低并减少计算的复杂度。
2 卷积神经网络结构
卷积神经网络(CNN)[12-13]是由猫的视觉系统得到启发发展而来,只有部分邻层神经元链处于兴奋状态,神经元的感知区域只感知局部而不是整个图像。CNN具有3个重要的思想架构分别为:局部区域感知,權重共享,空间或时间上的采样。
局部区域感知就是提取局部特征并得到某特征的空间分布。CNN的每一层通过多个特征map构成,每一层都能得到不同层级的表达式。权值策略的应用降低预训练参数,模型抗干扰能力和泛化作用进一步提高。采样的目的主要是混淆特征的具体位置,对变形和扭曲的图片进行识别。
卷积神经网络由卷积层提取出局部基本特征,由池化层进行组合构成更加抽象的特征,最后产生可以对图片对象直观描述的特征。图1为卷积神经网络的示例图。
将卷积网络学习得到的第1层特征输出,如图2所示,图中包括不同朝向与不同频率的边缘特征与颜色特征。
卷积层经过池化过程处理进入池化层,池化层计算窗口无重叠,Toolbox计算池化用卷积(conv2(A,K,'valid'))来实现,卷积核大小为2X2,元素为原来1/4,删除计算结果中的重叠部分,如图3所示。
通过全连接层,将卷积后的图片转化成向量形式,每个像素作为神经元节点。卷积层和池化层对图像数据的交替处理,大大提高了多维数据的处理能力。
3 粒子滤波框架
在本节中,基于上述外观模型,在粒子滤波的框架下,提出了一种基于稀疏子空间的卷积神经网络跟踪算法。基本思想是将基于CNN的稀疏子空间外观模型有效地融入到粒子滤波框架中,该框架通过Monte Carlo采样实现递归贝叶斯滤波。粒子滤波器主要是通过随机采样得到相关权重的粒子表示后验密度,粒子的权重决定了粒子的重要性。
粒子滤波器有两个主要部分:1)状态模型:根据以前的粒子生成候选样本;2)观察模型:计算候选样本的权值。给定对象对应时间的所有观测值y1:t=[y1,…,yt],基于粒子滤波器的跟踪系统的目的是估计p(xt|y1:t),它是目标状态的后验密度,用贝叶斯理论后验概率p(xt|y1:t)可以表示为
P(xt|y1:t)∝p(yt|xt)∫p(xt|xt-1)p(xt-1|y1:t)dxt-1(4)其中p(xt| xt-1)是状态模型,P(Ytl xt)是观测模型。积分的计算通过蒙特卡罗采样在粒子滤波器中进行。也就是说后验概率p(xt由一组粒子和相关的权重表示。最后,在t时刻最优对象状态xt*可以通过最大后验估计来确定:式中xt=(ptx,pty,ωt,ht),表示包括水平坐标、垂直坐标、宽度和高度在内的对象状态参数。
p(xt|xt-1)=N(xt:xt-1,∑)(6)其中∑是对角协方差矩阵,对角元素是相应参数的相应变化。对于每个状态xt,将图像块标准化为32×32像素的对应图像块。基于提出的稀疏子空间的卷积神经网络计算似然函数p(yt|xt)模型:
p(yt|xt)= exp(dt)(7)
目标状态表观由于会受到光流、视角和障碍物形变等不可抗因素的影响,随着时间的推移首帧信息形成的目标模型已不能适应当前的变化,可能导致跟踪的失败。为了捕获外观变化,似然函数需要随时间适应稀疏子空间的卷积神经网络外观模型更新,以达到良好的跟踪效果。为使得跟踪方法更加有效,在实验时每过5帧进行一次判断,置信度最大的粒子小于设定的阈值T(0.75)时进行更新,权重计算方法采用文献[10]中的方式。在每次更新时,保留首帧指定的目标模板,降低漂移现象的产生。实验结果表明,此更新方法与本文提出的基于稀疏子空间的卷积神经网络模型结合,能够准确捕捉表观变化,获得更加准确的结果。
4 实验过程及结果分析
4.1 跟踪过程的流程图与实验步骤
实验步骤:
初始化阶段(t=1):
1)在基于稀疏子空间的卷积神经网络模型中预训练数据;
2)手动获取第1帧的目标标签;
3)采集正负样本分别记为得到相应的模板;
4)调整每个模板的大小为32×32;
5)微调模型中的预训练正负样本;
6)初始化粒子滤波的目标状态和权重
7)设置相似度阈值T。
跟踪阶段:t=2:N
1)预测:for i=1,…,N1生成xti~p(xt|xt-1i);
2)可靠性估计:for i=1,…,N1,得到ωti=ωt-1ip(yt|xti):
3)检测目标的最优状态xt*并赋予粒子最大的权重;
4)重采样:归一化权重并计算归一化权重的协方差,如果该方差超过设定阈值则用最大权重的粒子替换最小权重的粒子。
5)当t为5的整数倍时,判断相似度大小,若相似度值小于设定的值T时,则进行模板的更新。
目标跟踪流程如图4所示。首先获取第一帧图像,通过粒子滤波器进行粒子的采样和分类,将基于CNN的稀疏子空间外观模型有效地融入到粒子滤波框架中,根据N的值判断相似度对模板进行更新。
4.2 实验结果与分析
仿真实验在Intel(R)COre(TM)i3-2310M CPU@2.10GHz电脑配置下通过对http://cvlab.hanyang.ac.kr/tracker_benchmark视频数据库的视频序列进行Matlab仿真完成。用以验证本文提出基于稀疏子空间的卷积神经网络目标跟踪算法。meanshift算法是一种具有一定代表性的经典目标跟踪算法,基于IVT的目标跟踪算法在以往的证明中效果相对最优,为验证算法的有效性,比较了meanshift目标跟踪算法和基于IVT的目标的仿真结果。仿真结果如图5和图6所示。在设置参数时,将文中测试阈值设置为0.75,通过大于阈值的部分可以反映跟踪效果。实验设计包括目标尺寸变化和短期目标遮挡下的目标跟踪。通过定性和定量分析跟踪算法证明了该算法在整体跟踪性能方面的优越性。
定性分析:
实验1:图5中黑色线框为本文算法,绿色框为meanshift跟踪算法,蓝色框为基于IVT跟踪算法,在冲浪者视频序列中,角色的上半身被选择作为跟踪目标,并且目标的初始位置是x5=(27713560120)。主要特点是目标位置在场景中变化和旋转并伴有尺度变化,选取1375帧,实验结果包含了视频帧中的50,90,170,240帧。
实验2:图6黑色线框是本文的算法,绿色框是meanshift目标跟踪算法,蓝色线框基于IVT目标跟踪算法,在所选择的视频序列中,选取人脸为目标,并且目标的初始位置为x0=(120557595)。主要特点是随着照明强度发生变化对目标追踪的影响。选取视频1~350帧,实验结果包含了视频帧中的50,90,170,240帧。仿真结果表明,该算法在复杂条件下追踪效果最好。
4.3 定量分析
图7~图9分别是本文算法与IVT目标跟踪和meanshift目标跟踪算法跟踪过程中的稳定曲线。在Matlab中用tic与toc口令计算对同一个视频序列(为节约时间只计算前350帧)进行跟踪的时间,图7用时18.1172s,图8用时24.6273s,图9用时28.7644s。根据实验时间本文算法在时间上得到提高,证明跟踪的快速性得到改善。在受到外部干扰的情况下,根据稳定曲线图分析,本文算法的波动幅度最小,证明稳定性得到提高。
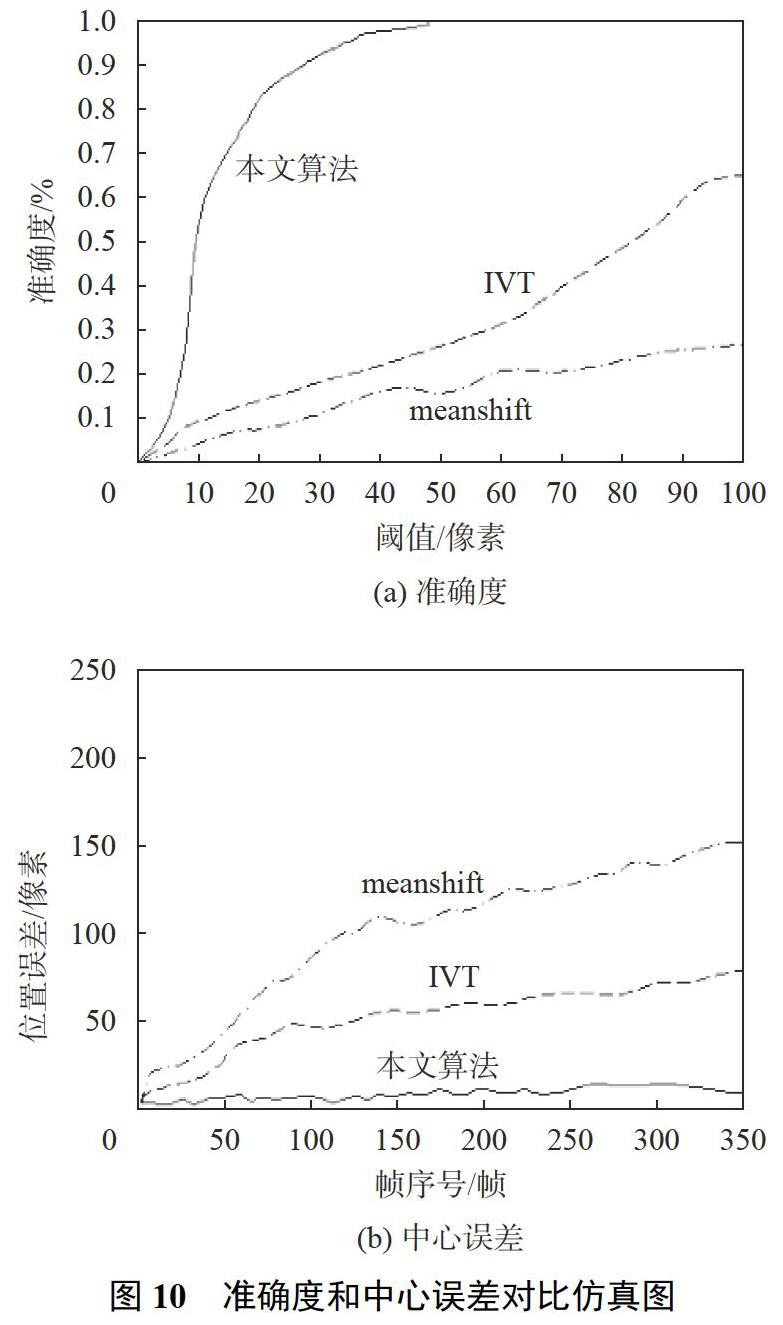
图10为根据对比参数准确度A和中心误差E得到的仿真图。式中n(p)表示中心位置点小于设定阈值p的帧数;Nf为总帧数,本文中取值为350;XC和YC为实际和跟踪结果的中心坐标。由图可以看出,该算法在准确度和中心误差方面优于其他两种算法。
5 结束语
本文在粒子滤波框架下提出一种基于稀疏子空间的卷积神经网络目标跟踪算法。该算法可以较好地处理局部遮挡、光照变化和尺度变化的影响,有着对多样本数据处理速度的优越性能,增强滤波模板目标和背景的分类能力。在复杂情况下,相比于meanshift目标跟踪算法和IVT的目标跟踪算法进行了仿真验证和分析。稀疏子空间模型对候选区域进行跟踪处理后,可缩短运算时间,减少计算量,具有较好的目标跟踪效果。当出现遮挡,光照和背景干扰的问题,卷积神经网络能很好地克服外界带来的干扰,准确进行跟踪,从而验证了算法的鲁棒性和准确性,在目标的识别和跟踪应用中具有一定实用价值。
参考文献
[1]WANG H,YUAN C,LUO G,et al.Action recognition usinglinear dynamic systems[J].Pattern Recognition,2013,46(6):1710-1718.
[2]YANG S,YUAN C,WAN(;H,et al.Combining sparseappearance features and dense motion features via random forest for action detection[C]//IEEE International Conferenceon Acoustics:IEEE,2013.
[3]张才千,葛磊,韩东.基于目标跟踪的粒子群粒子滤波算法研究[J].计算机仿真,2014,31(8):392-396.
[4]许伦辉,丛晓野.改进粒子滤波对人物跟踪的应用[J].计算机仿真,2014,31(1):344-347.
[5]许婉君,侯志强,余旺盛,等.基于顏色和空间信息的多特征融合目标跟踪算法[J].应用光学,2015,36(5):755-761.
[6]陈芸,吴飞,荆晓远,等.鲁棒低秩稀疏表示的在线目标跟踪[J].计算机工程与设计,2016,37(4):1062-1066.
[7]赵二群.视觉神经系统仿生模型及其应用研究[D].长沙:湖南大学,2014.
[8]HINAULT T,DUFAU S,LEMAIRE P.Strategy combinationin human cognition:a behavioral and ERP study inarithmetic[J].Psychonomic Bulletin&Review,2015,22(1):190-199.
[9]OLSHAUSEN B A,FIELD D J.Natural image statistics andefficient coding[J].Network,2009,7(2):333.
[10]王保宪,赵保军,唐林波,等.基于双向稀疏表示的鲁棒目标跟踪算法[J].物理学报,2014(23):174-184.
[11]YIN H.Sparse representation with learned multi-scaledictionary for image fusion[J].Neurocomputing,2015,148(148):600-610.
[12]DONG C,CHEN C L,HE K,et al.Image super-resolutionusing deep convolutional networks[J].IEEETransactions onPattern Analysis and Machine Intelligence,2016,38(2):295-307.
[13]KRIZHEVSKY A,SUTSKEVER I,HINTON G E.Imagendclassification with deep convolutional neural[C]//Advances inNeural Information Processing Systems,2012.
(编辑:莫婕)

