飞机轮速信号测试方法研究

艾波 闫文宇 李长江 任晓斌

摘要：为解决某飞机轮速信号测试中出现的数据缺失、曲线阶梯状不平滑及数据回零问题，分析轮速信号测试原理及测试系统结构，结合待测轮速信号特性，提出轮速信号测试优化方法，包括备份设计、直流隔离、周期测试及指标优化等。并针对轮速信号地面状态特性，设计一种信号测试链路检测方案。试飞测试验证结果表明，备份数据误差低于0.5%，数据曲线平滑，可消除数据回零现象，设计的轮速信号测试链路检测方案可行，有助于试飞航前检查。

关键词：试飞测试;轮速;优化;链路检测

中图分类号：V217 文献标志码：A 文章编号：1674-5124（2019）07-0025-06

收稿日期：2019-01-09;收到修改稿日期：2019-02-17

作者简介：艾波（1988-），男，陕西渭南市人，工程师，硕士，主要从事试飞机载测试工作。

0 引言

飞机轮速是飞机起落架、刹车控制系统的关键参数，对于评估起落架、刹车控制系统性能，实现飞机的地面精准操控[1-4]、确保试飞安全至关重要。同时，轮速与飞机的地面运动状态有关，能直观反映飞机起飞、着陆及由动至静的瞬时特性，因此它也是最小离地速度[5-6]、最大刹车能量[7]等特殊科目试飞的重要测试参数。

轮速信号测试可分为间接式和直接式两种。间接式即通过激光、超声波、多普勒雷达、卫星定位测速等方式测出飞机的地面运动速度，通过运动速度与轮速的换算关系求得。其中，多普勒雷达测速在可靠性、实时性、稳定性等方面具有明显的优势，在国外高速测量工程实践中已广泛应用[8-11];国内陈红江等[12]对地面测速进一步研究，设计的双天线雷达测速仪测速误差小于1km/h，具有较高的测量精度。直接式即在机轮上加装转速传感器[13]，将机轮的转速物理量转换为电信号，通常该电信号的频率与转速成正比，再通过测量该频率（周期）参数即可实现轮速信号测试。

在飞行试验中，由于多架次、数据监控需求，以及成本、资源限制等因素，轮速信号测试广泛采用直接式方式实现。而这种测量方式下，当飞机处于静止状态时，转速传感器无周期信号输出，因此频率（周期）测试数值显示为0。而按照当前试飞管理要求，航前参数检查普遍在地面进行，飞机处于静止状态，因此很难判断轮速信号测试状态是否正常，一般通过航后的数据分析判断。国内某型飞机试飞中，轮速信号测试也采用直接式测量，而处理轮速信号测试数据后发现存在3种问题：1）传输缺失一路轮速信号，2）部分轮速曲线呈现阶梯状的不平滑现象，3）飞机速度在70kn（1kn≈0.51m/s）左右时，信号出现回零现象。

针对轮速信号故障隐蔽性高、不易复现的特点，研究直接式轮速信号测试中的信号产生原理、测量原理、测试系统构成及测试链路特点，分析各环节影响因素，提出了备份设计、直流隔离、周期测试指标优化及链路检测方案，实现了轮速信号的检测与可靠测试，改善了轮速信号测试质量。

1 测试原理分析

直接式轮速信号测试系统一般由转速传感器、信号调节单元和测试单元3部分组成。

1.1 转速传感器

转速传感器用于将转速物理量转换为周期性的电信号，常见的有电磁感应式和霍尔效应式两种类型。电磁感应式转速传感器由一组线圈及电磁铁组成，机轮转动时带动随动齿轮转动，齿槽交替靠近电磁铁，使传感器所在电路的磁通量发生变化，产生周期性的感应电动势。一般传感器输出为正弦波信号，其频率与随动齿轮的齿数及齿轮转速有关，而通常齿数固定不变，因此输出正弦波的频率取决于齿轮转速，即机轮转速。霍尔效应式转速传感器主要由永磁体和霍尔元件组成，当恒定电流流过霍尔元件，且靠近永磁体时，在洛伦兹力的作用下产生一定的霍尔电压，通过测量单位时间内霍尔电压信号的次数，即信号频率，可以实现转速信号测试。

由此可见，这两种转速传感器的工作机理是机轮每转一圈发出固定个数的信号波形，从而信号频率与转速成正比。假设机轮每转一圈转速传感器发出K个波形，则当前转速N（r/s）与传感器输出信号的频率f（HZ）满足式（1）：

f=N×K（1）

1.2 信号调节单元

由于电磁环境影响和机械结构特性等原因，转速传感器输出信号一般是小幅值、非标准的正弦波信号，不便于直接进行周期（频率）参数测试。通常需要对传感器输出信号先进行调节，主要包括低通滤波、整形、电平转换，最终输出为标准TTL电平信号。因此，信号调节单元一般包括低通滤波电路、整形电路、电平输出电路及电源模块。低通滤波电路用于滤除高频分量、抑制干扰;整形电路一般由运算放大器、比较器电路组成，实现输入信号的放大和整形输出;电平输出电路将整形后的信号变换为标准TTL电平信号，以利于频率（周期）参数测试;电源模块是DC-DC转换电路，用于将外部激励电压（28V DC）转化为各电路模块所需的电压值。

1.3 测试单元

测试单元用于对信号调节单元输出的标准TTL信号的频率（周期）参数进行检测，通常有频率测试和周期测试两种方式。

1.3.1 频率测试

频率测试原理见图1，在已知时间段T₁内，对輸入的TTL信号的波形个数进行统计计数。假设TTL信号的周期为T_1s、频率为f_1s，T₁时间段内统计的TTL信号波形个数为N₁，则其关系满足：

通常T₁为测试单元内设定的计数时间间隔，若测试单元在to时刻启动计数器开始计数，则在（t₀+T₁）时刻停止计数，完成一次计数统计。由于待测TTL信号与测试单元中已知时间Tl的起始和终止时刻并不具有同步关系，因此计数器开始和停止计数的时刻不完全处于TTL信号的上升沿时刻，统计计数值N₁的误差最大绝对值为1。因此（2）可修正为：

由式（3）可知，当T₁一定时，统计计数值N₁越大，信号频率f_1s的计算值误差越小。因此，输入信号的频率越高、周期越小，频率测试方式计算的结果误差越小。

1.3.2 周期测试

周期测试原理见图2，在待测TTL信号的一个周期内，对已知脉冲的波形个数进行统计计数。假设TTL信号的周期为T_1s，频率为f_1s，已知脉冲的周期为T₂，在待测TTL信号的一个周期内所统计的已知脉冲波形个数为N₂，则其关系满足：

通常已知脉冲为测试单元内产生的高频矩形脉冲，其周期参数已知。当检测到TTL信号的上升沿时，计数器开始计数，而检测到TTL信号下一个上升沿时，计数器停止计数，完成一次计数统计。同样，由于待测TTL信号与已知脉冲并不具有同步关系，计数器开始和停止计数的时刻不完全处于已知脉冲的上升沿时刻，统计计数值N₂的误差最大为±1。因此式（4）可修正为：

由式（5）可知，礣T₂一定时，统计计数值N₂越大，信号频率f_1s的计算值误差越小。因此，输入信号的周期越大、频率越小，周期测试方式计算的结果误差越小。

2 测试方法优化

2.1 影响因素分析

2.1.1 转速传感器输出信号特性

设计厂商提供了飞机上加装的转速传感器技术资料，其输出信号特性见表1。

其中，交流信号峰-峰值V_min和V_max满足下式：

由表1可知，转速传感器输出的交流信号并非是“0均值”信号，而是具有一定的直流偏置电压，并且该直流偏置电压并非恒定量，而是随转速的变化而变化。

2.1.2 轮速信号测试系统

该飞机轮速信号测试系统结构见图3，结合转速传感器输出信号特性，分析该测试系统，有以下3种因素，会影响测试数据的准确性和可靠性。

1）单一转速传感器感知方式

转速传感器安装于起落架机轮上，处于刹车温度、机械运动、振动等多种特性于一体的复杂环境下。除飞机首飞等特殊科目要求不进行起落架收放操作，通常每个飞行架次都会实施起落架收放，使转速传感器信号链路的环境复杂度加剧，其测试线路可能会出现故障或松动，会导致无法捕获轮速数据。

2）信号调节单元设计基于“0均值”交流输入信号

常见的转速传感器输出信号都是“0均值”的交流信号，这种情况下该信号调节单元能正常检测周期信号，可以满足测试需求。当转速传感器的输出信号不具备“0均值”特性，而是具有一定量的直流偏置电压;或者该直流偏置电压非恒定量，而是随着转速的提高而增加，此时当转速提高到一定程度后，其输出的交流信号具有直流偏置电压（设为V_x）。而整形電路对于高电平信号的判别门限低于V_x时，则电平输出电路产生恒定高电平信号，即直流信号，而非TTL方波信号。此时，信号频率的实测值为0，从而会导致轮速信号测试值突然变为0。

3）信号测试方式及性能指标

该飞机的试飞机载测试系统采用DSI/003板卡对转换后的TTL信号进行周期（频率）测试，且配置为频率测试方式，式（3）中的已知时糡T₁设置为默认的1s作为计数基准。

一般飞机起飞速度为200～300km/h，以300km/h根据表1计算，最高信号频率约为2050Hz。同时，由于飞机的滑行过程都是始于或终止于相对静止状态，因此轮速信号以低频信号为主。文献[14]表明，对2050Hz及更低频率的交流信号进行频率（周期）测试时，宜采用周期测试方式。同时，以1s为频率测试计数基准时间时，决定了每1s对测试结果统计一次，因此存在阶梯状的不平滑现象。此外，由式（5）可知，计数器N值越大则测试数据误差越小，因此采用周期测试方式测量轮速时，应提高计数器计数结果N。

2.2 测试方法优化

针对上述3种影响因素，提出轮速信号测试的优化方法，主要包括备份设计、直流隔离、周期测试及指标优化。并针对轮速信号特性，设计一种信号测试链路检测方案，便于预先检查轮速信号测试链路状态，有助于测试排故工作。优化的轮速信号测试系统结构见图4。

2.2.1 备份设计

考虑起落架机轮的结构特性，在每个机轮中都加装两个转速传感器，并增加相应的物理链路和测试通道资源，形成备份的测试参数。机轮转动时，两个转速传感器独立工作，同时产生周期性交流信号，都能反映该机轮的转速特性。需要指出的是，互为备份的两个信号在试飞测试管理中作为两个参数存在，是一种增强可靠性的冗余设计方案，而并非是同一参数的两个信号源。在航后试飞数据分析时，由数据使用方决定这两个信号的使用方式。

2.2.2 直流隔离

信号调节单元设计中，在低通滤波电路前端增加直流隔离电容，以滤除其输入信号中的直流分量。滤除直流分量一方面能确保整形电路的输入基本为“0均值”的交流信号，经电平转换后，输出TTL信号的频率特性与原信号一致;另一方面能消除输入信号中的直流干扰，避免了经过放大器后造成的强干扰。

2.2.3 周期测试及指标优化

轮速信号主要为低频信号，根据文献[14]的分析应采用周期测试方式进行。对比周期测试方式下已知脉冲的信号周期指标，优化前的机载测试系统中采用了DSI/003测试板卡，其已知脉冲周期指标为9μs，优化后的机载测试系统改用DSI/102测试板卡，其已知脉冲的信号周期为40ns，降低为原来的1/225。因此，相同的输入信号特性下，周期测试中的计数器N值约为原来的225倍，有利于提高数据测量精度，减小误差。

2.2.4 测试链路检测

试飞航前检查时，机轮与地面处于相对静止状态，转速传感器无输出，轮速测试结果为0。因此，地面参数检查时一般难以预判轮速信号的正确性，往往在航后数据处理时才能发现轮速数据异常，通过排故过程定位问题。这种发现和定位故障具有一定的滞后性。

为降低这种滞后性影响，提前发现和解决测试链路问题，如图4所示，制作用于a点处与机上测试改装线缆对接的实验线缆（非装机线缆），通过该实验线缆将正弦波信号输入到测试系统，可以检查测试链路是否正常，有利于测试工程师在航前准备时快速确认信号链路状态。同理，分别制作用于b、c、d点的实验线缆，将正弦波信号输入到测试系统，可逐级检查后续设备、线缆是否正常，提高排故效率。

3 工程验证

为获取可靠、准确的轮速数据，在后续的飞行试验中采用了优化的轮速信号测试系统，主要进行的改进情况及其测试结果如下。

3.1 备份方案实现

通过与设计厂商沟通，在起落架上增加转速传感器，并增加相应物理链路和测试通道资源，形成备份的测试参数。在某次飞行试验中，从飞机滑行至起飞过程中选取12个测试点，数据结果见表2。

表中列举了2组共4个轮速信号，其中第一组WSPDL1、WSPDL2互为备份，第二组WSPDRI、WSPDR2互为备份。按照式（7）对这两组信号的相对误差[15]分别求期望值。其中，N为数据点数12，i=1，2，…，12。

第一、二组数据的相对误差期望值分别为-0.33和0.07%，低于0.50%，互为备份的两组信号特性基本一致，均能够满足试飞测试要求。若其中一路数据缺失时，备份数据可以作为有效数据使用，提高了数据测试的可靠性。

3.2 直流隔离实现

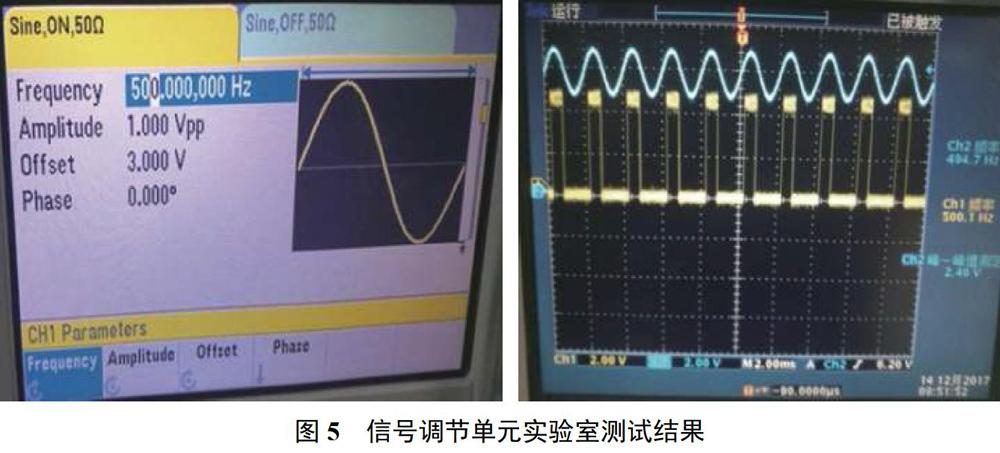
信号调节单元设计中，在输入接口与低通滤波电路之间增加了直流隔离电容，滤除其输入信号中的直流分量，实验室测试结果见图5。

实验中将频率为500Hz、峰一峰值为1V、直流偏置电压为3V的交流信号输入至信号调节单元，其输出为500.10Hz的TTL信号。实现了对输入信号的直流分量滤除，且输出信号的频率特性与输入信号基本一致。

3.3 周期测试及指标优化实现

优化的测试方案中改用DSI/102测试板卡对TTL信号进行频率（周期）测试，并设置为周期测试模式。该板卡产生的已知脉冲信号的周期为40ns，降低为原来的1/225，测试数据波形见图6和图7。

图6和图7的信号波形显示，轮速数据曲线平滑，未出现阶梯状现象。同时，速度为70kn时，轮速信号未出现回零现象，其实测值达到150kn以上。

3.4 测试链路检测方案实现

根据测试改装线缆的接口关系，选择对应的连接器，按接线定义要求制作了实验线缆（非装机线缆）。通过该实验线缆，可将便携式信号源MC5输出的正弦波信号输入至测试系统，通过检查轮速参数可快速实现轮速信号测试链路的航前检查。

4 结束语

针对飞机轮速信号测试现状，研究了直接式轮速信号测试原理及测试系统，分析了信号产生原理、测量原理、测试系统构成及测试链路特点，提出了备份设计、直流隔离、周期测试指标优化及链路检测方案，方案易于实现且成本低，实现了轮速信号的检测与可靠测试，对其他非"0均值”的交流信号、大型装备的轮速（转速）信号测试有重要的参考价值。然而研究内容还存在一些不足，比如尚未考虑转速传感器的校准方法，没有对转速传感器的输出进行标定，因此也未研究其對测试结果的影响，今后将研究转速传感器的校准方法，突破机上现场校准，检测传感器的输出状态，提高数据测试的准确性。

参考文献

[1]钱小妹.飞机操纵前轮转弯特性仿真研究[D].南京：南京航空航天大学，2008.

[2]ZHU D D，JIA Y H.Design of stability augmentor for aircraftnose wheel steering system based on Hopfield networkidentification algorithm[C]//2011 International Conference onElectric Information and Control Engineering，2011.

[3]WU H，CHEN T，WANG L，et al.Muti-wheel bogie brakingsystem simulation of civil aircraft[C]//National Conference onInformation Technology and Computer Science，2012.

[4]LI M，HAO X Y，HAN X F，et al.Aircraft landing gearsimulation using multidomain modeling technology[J].IEEE，2011（1）：279-281.

[5]张建.飞机最小离地速度试飞设计和风险控制技术[J].飞行力学，2014，32（6）：549-552，556.

[6]FAA.AC25-7B Flight test guide for certification of trans-portcategory airplanes[S].Washington：FAA，2011.

[7]何永乐，毕燕洪，赵文庆.飞机刹车能量确定方法和计算公式比较[J].飞机设计，2009，29（1）：44-46，56.

[8]周高杯.多运动目标的频谱分析及基于DSP的雷达测速仪的设计[D].长沙：湖南大学，2005.

[9]曲素荣，张中央，王留军一种新型铁路列车测速雷达的研究与应用[J].自动化仪表，2011，32（11）：56-58.

[10]李之果，张宇波，任军霞.基于DSP的交通雷达测速仪设计[J].电子技术应用，2009（4）：141-142.

[11]何佩琨，李琴，朱军，等.基于DSP的雷达车辆检测器的研制[J].北京理工大学学报，2004，24（8）：727-730.

[12]陈红江，张浩，汤灝，等.双天线雷达测速仪的研发[J].中国测试，2017，43（6）：75-78，113.

[13]李欣玉，梁品.转速传感器概述及可靠性测试方法研究[J].汽车电器，2016（8）：55-57.

[14]王晓勇，吕俊，王俊.基于DSP+FPGA的飞机轮速测量系统设计[J].2014，37（6）：131-134.

[15]王昌明，孔德仁，何云峰.传感与测试技术[M].北京：北京航空航天大学出社，2008：64-67.

（编辑：商丹丹）