地层水判定方法及数学模型应用研究

王 颖，解同川，呼桂艳，曹 宁，刘泽宇

（中国石油集团渤海钻探工程有限公司井下技术服务分公司，天津 300283）

获得地层水，是井下作业试油期间取得的重要参数之一。传统的判定方法是通过经验在恰当的时间取得水样，送至化验室做矿化度和水型分析，得出各个离子的含量。并通过经验判断大致符合该区块地层水性即为合格的水样。带有一定主观性，并且需要一定的时间充分的验证。那么及时、准确的判定出地层水就能够缩短试油周期，减少试油期间带来的多余的人力、物力及经济上的消耗。为油藏储量计算和开发提供可靠的资料[1，2]。

本论文利用统计规律，在某区块已有的水性资料充足的情况下，定量的设计出一个标准，当获得的待测水样越接近该标准，越能体现该地层真实的水性。从而快速判断出地层水的合格性和趋势性。

1 思路分析

首先，收集某一相同区块同层位相同水型的样品数据，以保证数据的可比性。再从中筛选出可靠的样品。由于真实的地层水水性的分布往往集中在某一范围内，所以远离该范围的数值有可能是异常值，会导致较大的误差，应予以剔除。通过运用格拉布斯准则，判断每一组水性离子中最大值或最小值是否为异常值，而予以剔除该样品。剔除异常值方法有多种，本文选取格拉布斯准则。因为每一离子所组成的样本空间数据相互独立，通过统计规律，符合正态分布。格拉布斯准则的运用，能使数据更加集中在该分布上[2，3]。

同一个样品内，各个离子之间数量级有的差异比较大，这就在模型建立过程中，高数量级的离子会遮盖低数量级的离子对矿化度的影响。将基础数据进行归一化处理，从而消除量纲影响[4]。

当在大量的数据统计中，真实的地层水显然集中在某个波动范围内，越是靠近真实地层水的样品，它们之间的距离越小。基于这样的思想，定量的建立出距离关系，用于比较和趋势观察。当所获得的待观测样品，落入这个波动分布范围中，显然是以较大的概率出现，即视为可靠的地层水水样。

同时，所取水样样品的前期可能混有井筒水或者压裂放喷时的压裂液等，会影响水性的稳定性，所以在后期不断排液取样而逐渐稳定，从而判断最佳的水样为该井的水性，以及各个离子的影响变化。若该井不出地层水，那么在趋势变化的曲线上必然在非地层水表示范围上。从而落实水性。

2 模型建立

2.1 建立数学空间

假设模型内共有m 个地层水的样品，每个样品内共有n 种离子a1，a2，…，an。样品中的离子含量的组成可视为一个Rn空间，那么m 个样品的各个离子含量可视为一个点集，样品空间的离子组成的矩阵Amn：

每个一维行向量（ai1ai2ai3…ain）可视为所取得的某个样品数据，每个一维列向量（a1ja2ja3j…amj）T可视为某一离子的样本空间的点集合。其中i=1，2，…，m；j=1，2，…，n。

2.2 筛选数据

假设某一离子样本空间点集合V=｛v1，v2，…，vm｝，样本v 相互独立，通过统计规律，该数据符合正态分布，按大小顺序排列，若为v1≤v2≤…≤vm，根据格拉布斯准则，异常值可能出现在最大值或最小值。若异常值为最小值v1，则有检验统计量：

确定显著水平α：若要求严格，检出水平α 可以定的小一些，例如定α=0.01，那么置信概率P=1-α=0.99；若要求不严格，α 可以定的大一些，例如定α=0.10，即P=0.90。

对于检验统计量G，当显著水平α 为1 %或5 %时临界值为G（n-1）（n），即格拉布斯系数。当最小值v1或最大值vm对应的统计量大于临界值时，认为与之对应的v1或vm为异常值，应予以剔除。相应的也就剔除该离子所在的样品[2，3]。

同理，其他水性离子包括总矿化度以此类推。总矿化度参与异常值剔除的意义在于各个离子的影响程度累加到总矿化度中时，矿化度也可能存在异常值问题。

2.3 数据归一化

假设某一离子的点集合V=｛v1，v2，…，vm｝，通过平均值法将数值v 归一化到[-1，1]范围内[5]，那么：

样本v 相互独立，通过统计规律，样本空间V 近似服从正态分布，通过归一化处理，由定理：一个随机变量的任何线性函数也是一个正态随机变量[6，7]，可得，样本v 能够映射到标准正态分布空间中，将[-1，1]定义为标准区间（见图1）。

式中：L-某一水样中各个离子到标准区间距离之和。

可见，L 值越小，越接近标准区间，也就是说，趋势是接近地层水的方向。

2.4 确定地层水（试油期间）矿化度应用取值范围

在大量的数据统计资料中，平均值反映了数据集中趋势，而离差的均方和体现样本离均值的波动程度。显然波动程度越小，越靠近地层水的真实情况。同时，为了消除量纲的影响，均用归一化后的数据。

在Amn中，每种离子的平均值设为归一化后，设为，其中j=1，2，…，n。

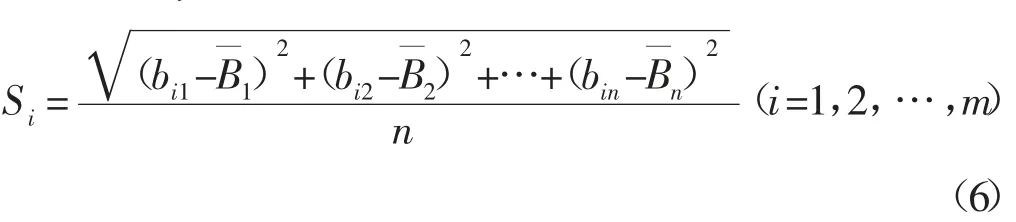
式中：Si-第i 个样本地层水矿化度分布；bi1、bi2、…、bin-第i 个样本m 个离子归一化数值；-n 个样本中每种离子均值的归一化数值。

在m 个样本中，由{Si}获得某一区块地层水矿化度主要集中的分布范围，设为[a，b]。

若某一实际水样样品观测值经过基础数据归一化后其S 值落入[a，b]内，可视为该地层水的水样样品是可靠的。

2.5 在可靠的水样样品中进行对比，选择最优水样样品

2.6 判断水样样品数据的变化趋势

样品序号作为X 轴，S 值作为Y 轴，得到S 值的变化曲线，当曲线在[a，b]范围内波动，可以判断获得稳定的地层水；若曲线在[a，b]范围外，或在其范围内外成波浪线，可以判断为非地层水。

3 实例分析

以下结合实例对本文所述的方法做进一步阐述，通过实际技术操作做出更准确和深入的理解。

3.1 数据收集

收集到大港油田板桥地区沙二段，包括滨二、滨三、滨四层位的82 口井228 个水性样品进行统计，评价离子为七种离子，水型为NaHCO3。

3.2 筛选样本

每一离子（包括总矿化度）所组成的样本空间，运用格拉布斯准则，在显著水平α 为1 %条件下，剔除异常值，每操作一次，剔除一个值及该值所在的样品。直到“没有检测出异常值”。再进行下一组列数据检测。通过检测筛选出158 个水性样品。并计算出各个评价离子的平均值，其中j=1，2，…，7。

3.3 数据归一化处理

将各个离子的数据集合作为一个子样本空间，由公式（2）、（3）分别归一化到[-1，1]的区间内。由大量数据统计规律可得，归一化后的数据符合标准正态分布。在其分布曲线中，越接近0 点（即中间均值），且距离大小以定量形式表示出来。同样得出各个评价离子的归一化的平均值，其中j=1，2，…，7。即={-0.25 -0.45 -0.4 -0.38 -0.3 -0.78 -0.05 -0.14}。

3.4 确定地层水的标准范围并进行实例分析

利用前述公式（6），计算出每个样品S 值，将归一化的矿化度值作为X 轴，S 值作为Y 轴，可得S 值的散点分布（见图2）。

图2 S 值散点分布图

从图2 看出，S 值集中分布在区间[0.05，0.31]，故取S 值[a，b]为[0，0.31]。

板深43×1 井是2015 年在天津市大港区港东地区实施的一口预探井。层位为滨四，160、166、167 号层，射孔井段4 434.5 m～4 472.7 m，17.8 米/3 层，电测解释油层、差油层。该井射孔后进行了压裂施工、放喷作业。放喷第9 天开始连续8 天取了10 个水样（见表1）。

表1 归一化处理后数据（见表2）。将样品序号作为X 轴，S 值作为Y 轴，得到S 值的变化曲线（见图3）。

表1 板深43×1 井水样原始数据

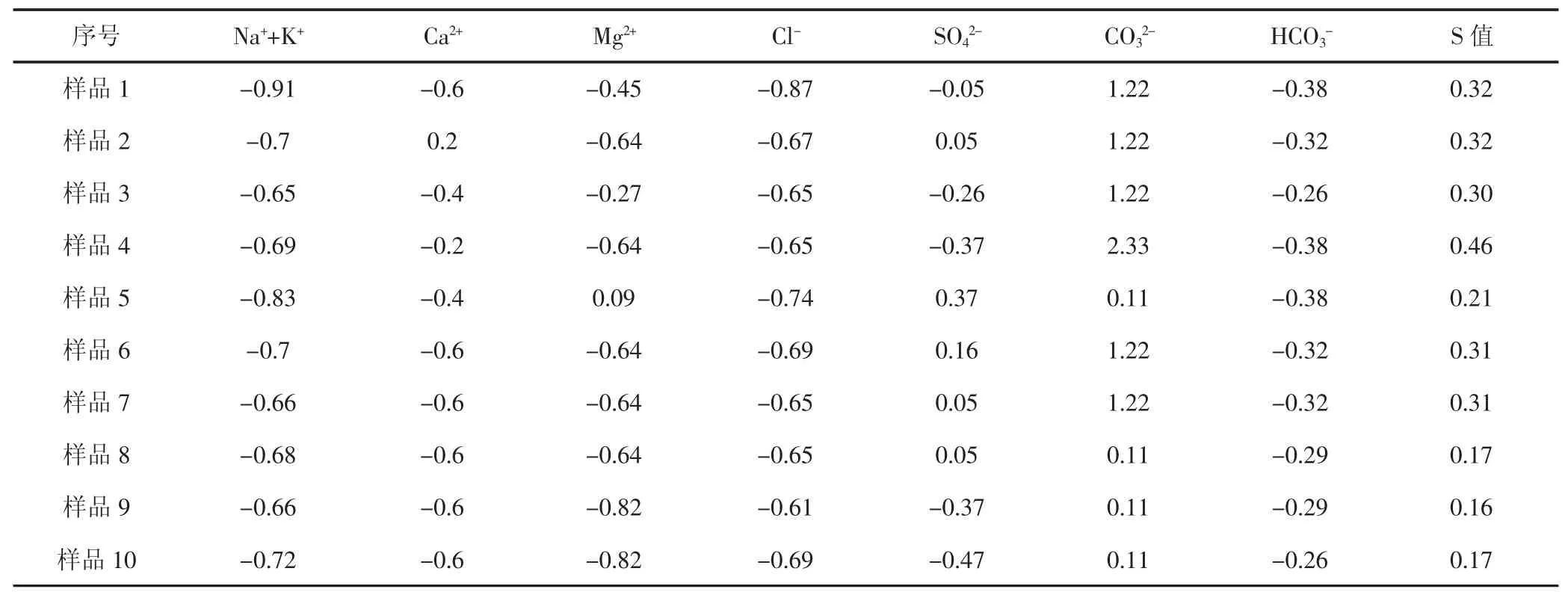
表2 板深43×1 井水样归一化数据

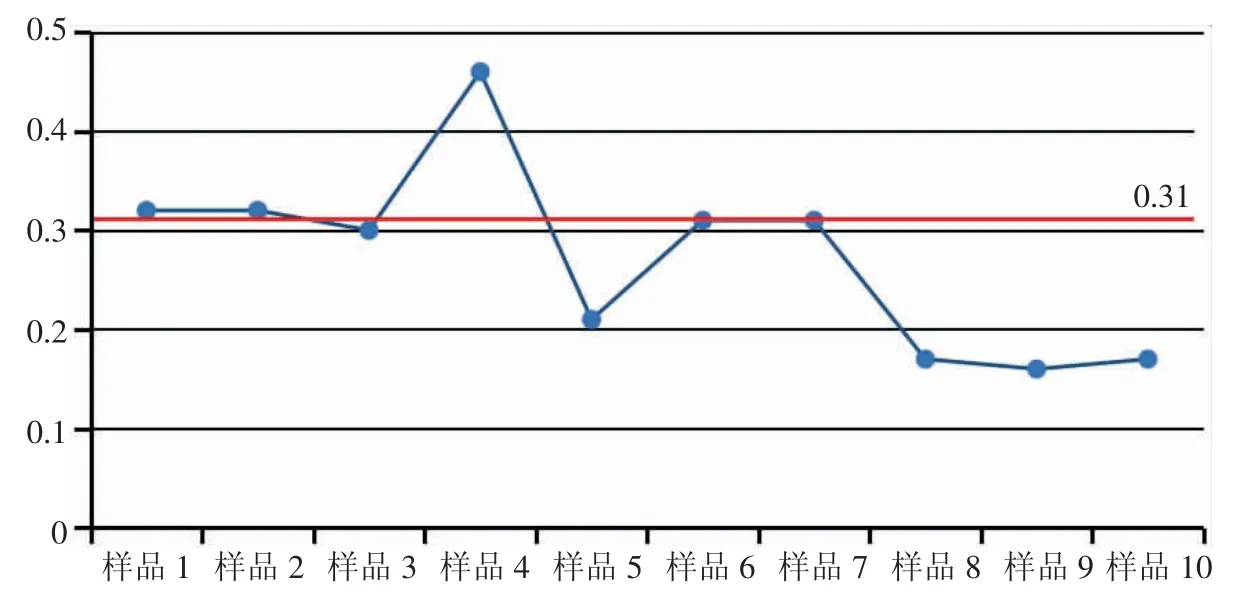
图3 板深43×1 井S 值折线图

图4 板深43×1 井水样归一化数据折线图

由图3 可得，该曲线呈波浪线，后期曲线S 值落入[0，0.31]范围内，所以总体趋势是趋向地层水的，并且越来越稳定。样品1、样品2、样品4，3 个水样显然未落入[0，0.31]区间内，是需要舍弃的数值。前5 个水样成为不稳定的波浪线，后5 个水样落入区间内，逐渐趋于稳定，为该井层位的水性提供备选。

在这5 个水样中，由公式（7），S 值越小，与平均值差异性就越小，即为最优水样。从图3 看，样品9 是合适的。实际施工中，通过经验判断选择的是第10 个水样。可见经验判断仍然存在一定的盲目性。

将表2 以折线图方式表示出来，观察各个离子变化（见图4）。观察到，第1、2、3、4、6、7 个水样的超出[-1，1]区间的临界值，应给予高度重视，该离子的异常变化可再做进一步分析。尽管如此，3、6、7 水样中，S值仍然有效，所以单个离子超出临界值并不能完全否认该水样的可靠性。由表2，运用前述公式（6），得与平均值之间的差距（见表3），相应的折线图（见图5）。

由图5 可知，各个曲线越接近0 线，越接近平均值地层水。同时，各个离子中，变化幅度最大，是影响地层水的关键因素，应高度重视，并且可以做进一步分析。

表3 板深43×1 井水样与平均值之差距

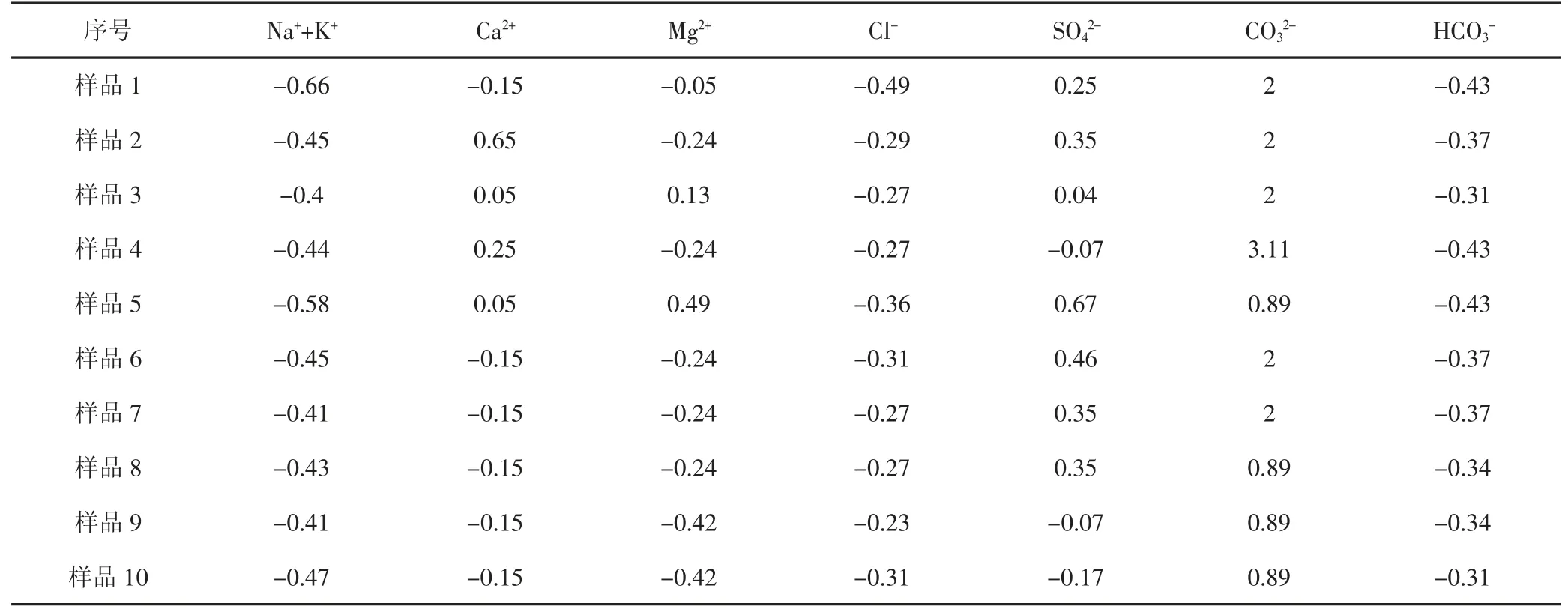
表3 板深43×1 井水样与平均值之差距

图5 板深43×1 水样与平均值之距离图

4 总结

（1）通过试验验证，待测水样与该区块相应层位水性之间的距离差异越小，越趋向地层水。当落入标准区间内，则可以判定为地层水，并且找到最优选值。另一方面通过局部分析，找出差异性大的离子做影响水性的进一步分析。

（2）本方法在实施中基础数据的可靠性非常关键，特别是在实际取水样做化验时，要及时有效，以免人为不必要的误差，比如放置时间过长易被氧化。并且取样时间顺序务必正确，以便做出趋势观察。

（3）当地层水混入其他液体时，如泥浆水、压裂液、动力液、压井液、射孔液等，通过定量比较，都可以很快的判断出排液后取得的水样变化趋势，在合适的时间点上判断出是否是地层水，从而落实水性。