基于改进烟花算法的非线性模拟电路测试激励优化

吴世浩 孟亚峰 王超

摘要：为增强非线性模拟电路故障诊断中故障模式之间的可辨识性，提高故障诊断率，提出一种基于改进烟花算法的非线性模拟电路测试激励优化方法。该方法首先采用基于Volterra频域核和BP神经网络的方法对非线性模拟电路进行建模，进而针对烟花算法存在寻优速度慢、效率低等问题，对其爆炸算子、变异算子、选择策略等进行改进，采用改进后的烟花算法对非线性模拟电路的测试激励进行寻优，通过电路仿真表明，优化后的信号可有效提高故障可分性，从而提高故障诊断率。

关键词：Volterra级数;BP神经网络;非线性模拟电路;烟花算法

中图分类号：TV641 文献标志码：A 文章编号：1674-5124（2019）06-0138-08

收稿日期：2018-03-02;收到修改稿日期：2018-04-13

基金项目：国家自然科学基金（61372039）

作者简介：吴世浩（1993-），男，河南焦作市人，硕士研究生，专业方向为装备测试与故障诊断。

通信作者：孟亚峰（1970-），男，河北石家庄市人，副教授，博士，主要从事电子装备性能监测与故障诊断。

0 引言

由于非线性模拟电路中的元件存在非线性、容差性等原因，导致电路发生故障时故障特征区分不明显，诊断困难。在对电路进行故障诊断时，不同测试激励下，电路的响应不同，优化测试激励信号可以降低故障特征的模糊性，从根源上改善故障特征，从而提高故障诊断精度和效率[1]，在非线性模拟电路故障诊断中具有重要作用。

文献[2]选取多音信号对非线性电路进行激励，但获取的故障特征仍存在混叠的问题;文献[3]采用多变量自适应回归样条函数对非线性电路建模，同时将遗传算法引入激励优化，效果显著，为非线性模拟电路激励优化提供了新的思路;文献[4]将智能算法引入基于Volterra级数的故障诊断中，提出一种尽量少的激励信号生成尽量多的特征频率的信号设计方法，但找到的最优激励为局部最优;文献[5]采用退火遗传混合算法对非线性模拟电路的测试激励进行寻优，但没有模型进行分析，同时没有对寻找到的激励信号进行诊断效果的检验;文献[6]采用灵敏度分析对确定了激励信号的频率分量，提高了故障诊断的精确度，但该方法比较复杂，对于规模较大的非线性电路难以实现。

可以看出，寻找最佳测试激励信号是非线性模拟电路故障诊断中的一个重要方向，但仍存在不少问题。本文利用Volterra级数可有效表征非线性模拟电路的特点[7]，结合BP神经网络，实现对非线性模拟电路的准确建模，在此基础上，采用比較新颖的烟花算法（fireworks algorithm，FWA）对测试激励信号进行寻优，并根据FWA存在的问题进行改进，设计了更适用于测试激励信号寻优的爆炸算子、变异算子、选择策略等，并采用各故障间的欧氏距离来构造适应度函数，从而实现测试激励信号的优化。

1 基于Volterra-BPNN的非线性模拟电路建模

Volterra级数理论上可以任意逼近一个连续函数，类似于线性系统的传递函数，能够直观反映非线性系统的特性[8]。其频域核只与系统自身的特征参数有关，不会随着系统输入的改变而发生改变，具有鲁棒性较强、对激励信号的特性没有限制等特点，可使人们直观、准确地理解许多非线性现象，具有较高的可靠性。

BP神经网络具有逼近任意非线性函数的特点，且输入节点灵活，训练方便，在非线性模拟电路中，频率成分的个数不同，对应着不同阶的Volterra频域核，BP神经网络的特性适用于基于Volterra级数的非线性电路建模。首先准确测量非线性模拟电路的Volterra频域核值[9]，在此基础上，利用BP神经网络对非线性模拟电路进行建模。将频率成分及对应的频域核幅值作为输入输出数据，对BP神经网络进行训练，采用BP神经网络对非线性系统前N阶频域核进行辨识模型时，需要建立N个神经网络模型，如图1所示。

图1中，ω₁，ω₂，…，ω_N为输入的频率成分，H_N（ω₁，ω₂，…，ω_N）为对应的Volterra频域核值，其中，一阶频域核神经网络模型输入层结点数为1，二阶频域核神经网络模型输入层结点数为2，三阶频域核神经网络模型输入层结点数为3，以此类推。

训练好模型后，响应获取任意阶的Volterra频域核值，只要将对应的频点坐标输入模型即可获得。以前3阶频域核辨识为例，多音激励下基于神经网络的Volterra频域核辨识流程如图2所示。

具体流程为

1）对被测非线性模拟电路进行扫频分析，确定有效频率范围。

2）采用多音信号频率基搜索算法搜索多组多音激励信号。

3）在幅值范围内改变多音信号幅值对非线性电路进行激励（激励次数不小于多音信号的音数），并对输出信号进行采集，由Vandermonde法[7]测量前3阶频域核。

4）根据前3阶频域核特点分别设计3个BP神经网络结构，将各频率组合对应的频域核值输入到神经网络中进行训练，隐含层神经元个数通过平均相对误差和决定系数来确定，从而获得各阶Volterra频域核的神经网络模型。

2 改进烟花算法

FWA是由Tan和Zhu于2010年提出的一种新型智能算法[10]，具有很好的局部搜索能力和全局搜索能力，可有效避免算法早熟问题，并具有较高的求解稳定性，在多个领域得到广泛应用[11-13]。

2.1 标准烟花算法

FWA采用并行搜索方法，寻优过程中，每个烟花作为爆炸点，按一定的规则向周围产生火花，符合要求的火花作为新的烟花，继续对空间进行搜索，直至寻找到最优值或达到迭代次数。标准的FWA主要流程如图3所示[14]。

FWA主要由爆炸算子、变异算子、选择策略3部分组成。爆炸算子是FWA的核心，其中包括爆炸幅度、爆炸火花数目和位移操作。烟花通过爆炸可以产生若干火花，对于烟花xi，其爆炸幅度Ai和爆炸火花数目S_i的计算公式分别为式中：A——常数，表示烟花最大爆炸幅度;

M——常数，用来控制爆炸产生火花的数目;

y_max，y_min——当前种群中最好个体的适应度值和最差个体的适应度值;

ε——避免除零操作。

从式（1）和式（2）中可以看到，适应度值较好的烟花可以产生较多的火花，爆炸幅度较小，局部搜索能力强，适应度值较差的烟花产生较少的火花，但爆炸幅度较大，有利于全局搜索。

为避免爆炸火花过多或过少，定义火花数量限制公式如下：式中：S_i——实际产生的火花数目;

a、b——控制花火规模边界的参数;

round（）——四舍五入取整函数。

位移操作公式如下：式中：x_ik——第i个个体在第k维上的位置;rand（）——生成随机数。

为增加爆炸火花多样性，引入高斯变异操作，公式如下：式中：gauss——服从均值为1，方差为1的高斯分布;

x_ik——第i个烟花在第k维的位置。

FWA的选择策略中，首先保留适应度值最好的个体，再采用欧氏距离计算任意两个个体之间的距离，采用轮盘赌法对剩下的个体进行选择，计算公式为式中：p（x_i）——个体被选择的概率;

R（x_i）——个体与其他个体之间的欧氏距离。

选择出来的个体作为新一代的烟火重新进行爆炸、变异、选择操作。

2.2 算法分析与改进

采用FWA寻优时，发现其存在耗时较长、效率较低等缺点，结合非线性模拟电路测试激励优化问题，对FWA进行改进。

1）爆炸幅度改进

式（1）保证了适应度值好的个体爆炸幅度小，目的是加强局部搜索，然而实验过程中发现，适应度值高的个体的爆炸幅度几乎为零，对爆炸幅度进行分析，将最优个体适应度值代入式（1）中得到：

由于E为非常小的常数，由式（8）可以得到此时爆炸幅度Ai趋于0，可以认为，最优个体进行爆炸操作时，几乎原样复制，而由式（2）可知最优个体产生的火花数量最多，相互之间欧氏距離很小，采用式（6）进行选择时，几乎全被淘汰，既消耗了时间，也没有产生好的效果，文献[15]对爆炸幅度改进如下：式中：t——爆炸搜索代数;

T——总的搜索代数;

A_min——爆炸半径最小值。

这种方法寻优前期爆炸幅度大，利于全局寻优，后期爆炸幅度小，利于局部寻优，但该方法每一次迭代，产生的个体无论适应度值好坏，爆炸幅度均一致，不能很好地反映个体的差异性，因此本文将个体的适应度值大小考虑进去，对式（9）进行改进：其中，f_avg（x）为当前代数所有个体的平均适应度值的。由式（10）可以看到，该方法产生的爆炸幅度不仅随迭代次数的增加逐渐减小，每代中不同烟花所产生的爆炸幅度也不同，这增加了烟花的差异性，有利于寻优。

2）爆炸火花数目生成

寻找非线性模拟电路最优测试激励信号的过程，是使故障类型区分最大，即寻找适应度函数的最大值，当适应度函数较大时产生的火花数目应当较多，仍采用标准算法中的方法，将式（2）而转换为

3）变异算子改进

高斯变异增加种群多样性，式（5）选择任意烟花进行变异，事实上，适应度值低的烟花具有较大的爆炸幅度，可对空间进行搜索，为使所有烟花中适应度值高且数目多的烟花产生变异以利于提高生成更优良烟花的概率，因此将式（5）改进为其中x_ibest^k为当前最优烟花在第k维上的位置。

4）选择策略改进

标准FWA中的选择策略是基于个体之间的欧式距离进行筛选，而适应度值高的烟花爆炸产生的火花间距离较近，在采用式（6）进行筛选时，很多好的火花被摒弃，同时增加了时间消耗，本文采用精英选择策略对烟花进行筛选，公式如下所示：

可以看到，适应度值高的烟花被选择的概率大，当前种群中适应度值最高的烟花被选择的概率为1，直接保留到下一代。

5）适应度函数构造

设电路有N种故障状态，则每个输入信号通过神经网络模型获得N个Volterra频域核，即N个故障状态矢量，以各状态矢量之间的欧氏距离总和作为适应度函数，来对激励信号进行优选。适应度函数表达式为式中：J——电路适应度函数;

H_j和H_jj——某激励下的各故障状态响应;

‖H_j-H_ij‖——各故障状态矢量之间的欧氏距离。

本文中的适应度值函数考虑了各故障特征相互之间的关系，当适应度函数J最大时，各故障类型的可分性最好，越有利于故障诊断。

基于改进烟花算法的测试激励优化流程如下：

1）对被测非线性模拟电路进行分析，采用第1节提出来的基于Volterra-BPNN的建模方法对电路进行建模;

2）根据寻优信号的音数确定烟花算法中的维度，同时设定爆炸产生最大火花数目及最小火花数目、爆炸最大幅度、变异火花数、最大迭代次数等参数，同时根据电路有效频率范围设定搜索空间;

3）计算初始烟花种群的适应度值，适应度函数构造方法如式（14）所示，由式（11）确定各烟花爆炸产生的火花数目;

4）由式（10）确定各烟花的爆炸幅度，计算产生火花的适应度值;

5）根据式（12），从适应度值最高的火花中选择个体进行高斯变异，产生变异火花;

6）采用式（13）对烟花、子代火花、变异火花进行选择，将结果存到下一代，循环到满足停止条件或达到循环次数，结束。至此，输出结果即为最优测试激励信号，此时的适应度值即为各故障之间的最大距离。

3 仿真验证

本文以典型的非线性电路低通滤波器为例，进行仿真验证，如图4所示。

该低通滤波器中，电源u₁为可编辑激励信号源，R₁为10Ω，C₁为4.7μF，C₁和R₂两端的电压同为u₂，u₂为系统电压输出值，流过R₁和R₂的电流分别为i₁和i₂。非线性电阻R₂的伏安特性表示为：i₂=0.001×（u₂+5u₂²）。设激励信号为u（t）=a（cos（2πf₁t）+cos（2πf₂t）+cos（2πf₃t）），在PSpice環境下扫频及参数扫描分析得有效频率范围为0～3.4kHz。

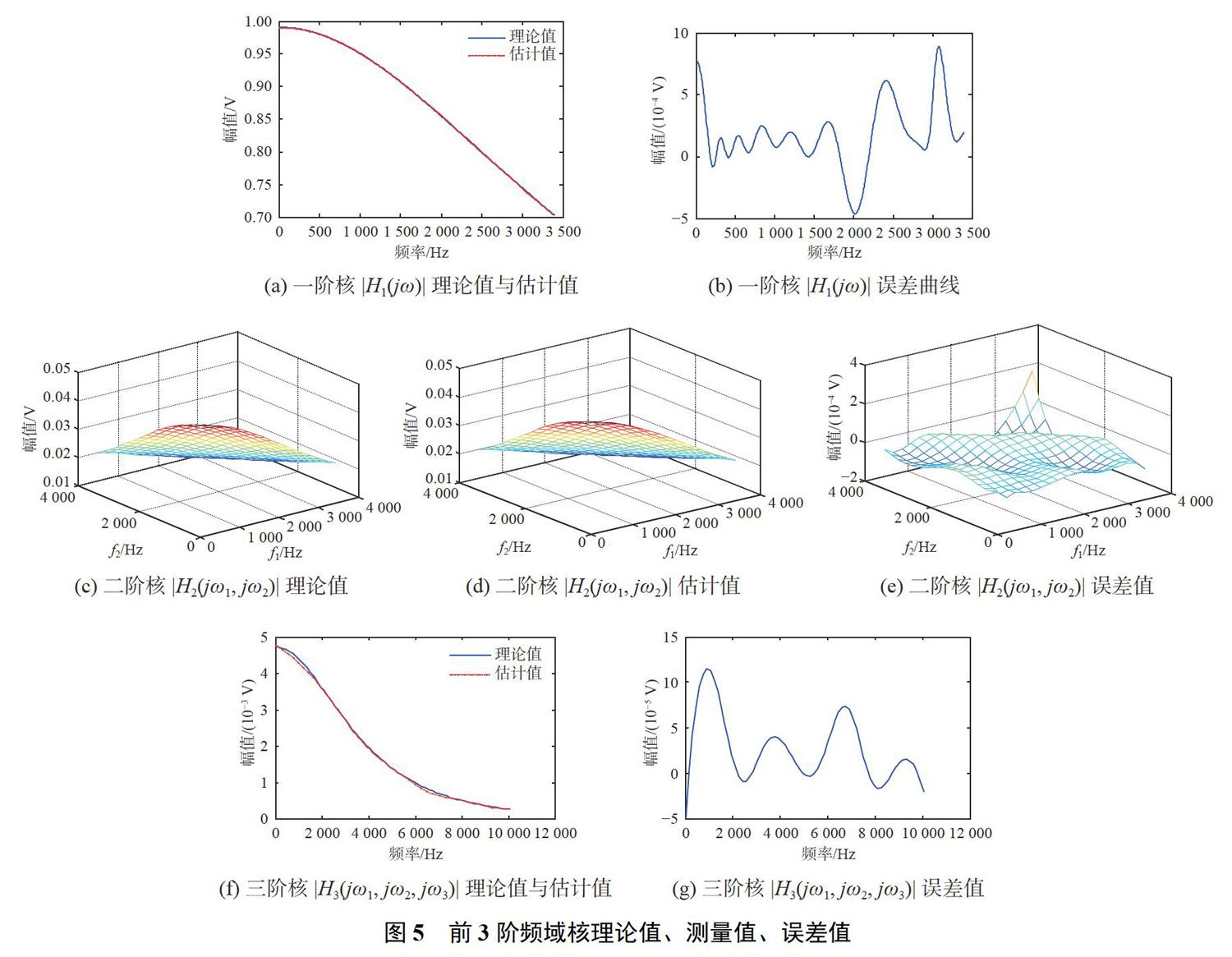
在频率范围内，采用多音信号搜索方法搜索得到20组多音信号（频率成分尽量分布均匀），采用第1节中提到的流程对电路进行建模，以无故障状态为例，将获得的频率值输入，再取300个频率对模型进行验证。前3阶频域核理论值、测量值和误差值分别如图5所示。

从而得到，一阶核最大误差值为0.00087V，二阶核最大误差值为0.000 23V，三阶核最大误差值为0.00012V，精度较高，说明基于Volterra-BPNN建模方法的有效性。

基于此模型，采用改进FWA对该电路的测试激励进行寻优。由于硬故障的特征明显，易于诊断，本文只对软故障的情况进行分析。将电路设置6种待诊断故障状态，如表1所示。

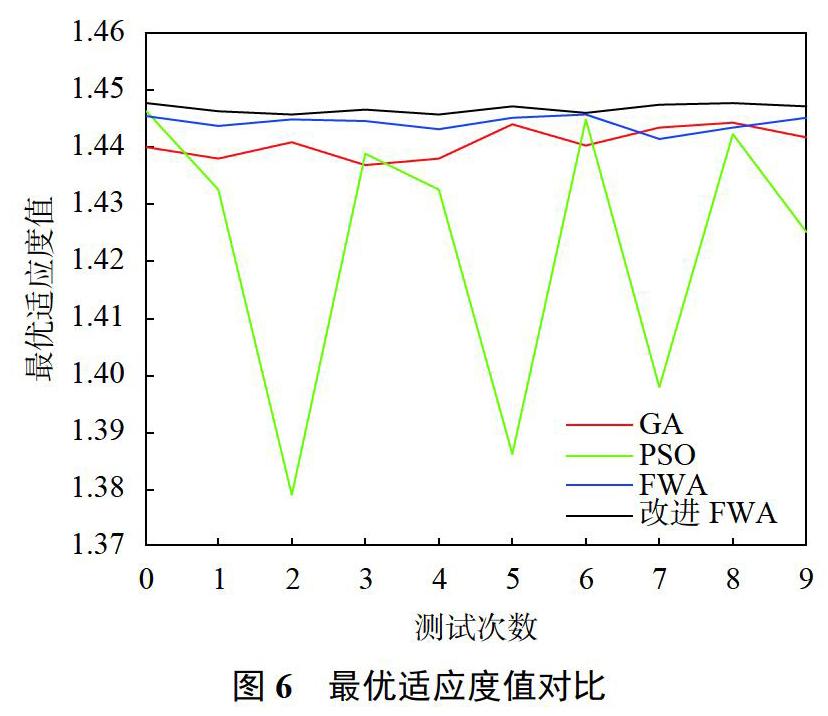
由于输入信号为三音信号，故烟花的维度为3维，设定初始烟花个数为5，爆炸产生最大火花数目为50，变异火花数目为5，迭代次数为40，频率搜索范围为0～3.4kHz，重复10次操作，将每次搜索得到的最优适应度值和消耗时间与遗传算法（GA）、粒子群算法（PSO）和标准烟花算法（FWA）进行对比，如图6和图7所示，为更好地对比各算法的性能，分别计算各算法结果的平均值、方差和运行平均时间如表2所示。

由图6、图7和表2可以看到，GA寻优的速度较快，平均时间为840.95838s，但寻优效果一般，适应度函数的平均值和方差分别为1.4408V和7.1440×10^-6V2;采用PSO进行寻优过程中，容易陷入局部最优，导致其平均值和方差在4个方法中最差，分别为1.4227V和6.4310×10^-4V²;FWA本身寻优能力较强，稳定性较好，适应度函数的平均值为1.4443V，方差为1.6988×10^-6V²，但消耗时间过长，平均消耗时间达1516.1166s，改进后FWA寻优效果得到加强，适应度函数的均值和方差均为最优，分别为1.4469V和6.8400×10^-7V²，消耗时间也大幅缩减，与GA速度相当，通过对FWA的爆炸算子、变异算子和选择策略的改进，FWA在寻优效果和寻优速度上都得到了加强。

将优化后的激励信号输入到电路中，通过诊断进一步检验采用改进烟花算法寻优的效果。优化后的激励信号为{3399.9883，3399.6913，3365.8461}Hz。将该激励信号输入到被测电路中，根据Volterra级数特性，产生的前3阶频域核对应的频率成分如表3所示。

其中一阶频域核对应3个频率成分，二阶频域核对应9个频率成分，三阶频域核对应19个频率成分，所以在此激励信号下产生的故障特征为31维，故障特征值为各阶频域核中各频率点对应的幅值。

将电阻和电容的容错值分别设为5%，设置电路的各种故障状态，分别进行50次蒙特卡罗仿真，提取到各维故障特征，如图8所示。

采用任取30次故障特征对SVM进行训练，其余20次故障特征进行检验，并与其他算法搜索的结果进行对比，如表4所示。

采用改进FWA寻优结果对电路进行激励时，故障诊断率最高，达99.17%，仅有状态F₃中出现一次误诊，误诊为故障F₄;采用GA和FWA优化方法得到平均故障诊断率均为98.33%，状态F₃各出现两次误诊;采用PSO优化方法得到的平均故障诊断率最低，为97.5%，除了状态F₃出现两次误诊外，状态F₀也出现一次误诊。

4 结束语

本文针对非线性模拟电路的测试激励优化问题进行研究，提出了基于改进烟花算法的测试激励优化方法，首先对非线性模拟电路的建模方法进行研究，在此基础上，针对烟花算法存在的问题，对其爆炸幅度、变异算子、选择策略等进行改进，采用改进后的烟花算法对测试激励进行寻优。仿真实验表明，本文提出的基于Volterra-BPNN的建模方法可以实现对非线性模拟电路的准确建模，本文对烟花算法的改进不仅提高了算法的速度和稳定性，其寻优的性能也得到加强，能够寻找到使各故障状态距离最大的测试激励信号，有效提高了非线性模拟电路的故障诊断率。

参考文献

[1]赵鹏.模拟电路测点优选与测试生成方法研究[D].南京：南京航空航天大学，2010.

[2]CHUA L O，LIAO Y L.Measuring Volterra kernel[J].International Journal of Circuit Theoty and Applications，1989，17（2）：151-190.

[3]VARIYAM V N，CHERUBAL S，CHATTERJEE A.Prediction of analog performance parameters using fasttransient testing[J].IEEE Transactions on Computer-AidedDesign of Integrated Circuits and Systems，2006，21（3）：349-361.

[4]殷时蓉.基于Volterra级数和神经网络的非线性电路故障诊断研究[D].成都：电子科技大学，2007.

[5]林海军，张礼勇，顾耕，等.基于退火遗传混合算法的模拟电路诊断激励优化[J].电测与仪表，2009，46（12）：17-19.

[6]韩海涛，马红光，谭力宁.基于灵敏度分析及Volterra级数的非线性模拟电路故障诊断[J].电路系統学报，2013，18（1）：17-22.

[7]孔祥玉，马红光，韩崇昭.非线性系统建模及故障诊断应用[M].北京：科学出版社，2014：125-144.

[8]卫小娟，丁旺才，李宁洲，等.基于改进粒子群算法的Volterra模型参数辨识[J].振动与冲击，2015，34（21）：105-112.

[9]HAN H T，MA H G，TAN L N，et al.Non-parametricidentification method of Volterra kernels for nonlinear systemsexcited by multitone signal[J].Asian Journal of Control，2014，16（2）：519-529.

[10]TAN Y，ZHi]Y.Fireworks algorithm for optimization[C]//ICSI.Berlin：Springer，2010：355-364.

[11]ZHANG B，ZHANG M X，ZHENG Y J.A hybridbiogeography-based optimization and fireworks algorithm[C]//CEC，2014：3200-3206.

[12]黄伟建，郭芳.基于烟花算法的云计算多目标任务调度[J].计算机应用研究，2017，34（6）：1718-1720.

[13]王啸，韩太林，张恩奎，等.基于烟花算法的压阻式压力传感器动态补偿方法[J].兵工学报，2017，38（11）：2226-2233.

[14]谭营，郑少秋.烟花算法研究进展[J].智能系统学报，2014，9（5）：515-528.

[15]杜振鑫.烟花算法中爆炸半径的改进研究[J].计算机时代，2013（1）：28-29.

（编辑：徐柳）