0.35 μm高速真随机数芯片设计

侯二林，朱 翔，冯纯益，张建国，王云才

(1.太原理工大学 新型传感器与智能控制教育部和山西省重点实验室，太原 030024；2.成都三零嘉微电子有限公司，四川 成都 610041)

随机数被广泛应用于现代密码系统中，作为安全密钥使用。根据产生方法的不同，随机数主要分为两类：伪随机数和真随机数。利用CPU运算某种数学算法(如线性同余算法)可以快速地生成伪随机数，然而伪随机数具有周期性，可以被预测，无法确保密码系统的安全[1]。真随机数是一组具有不可被预测性和不可复制性的数字序列，它不依赖于数学算法，无法从已知的初始条件中预测出下一位数字，因而具有良好的保密性[2]。真随机数通常是从物理随机过程(熵源)中提取，如热噪声[3]、振荡器相位噪声[4]、光量子噪声[5]、原子核放射性衰变[6]以及混沌电路[7]等，其产生装置被称为真随机数发生器(true random number generator，TRNG).

基于混沌电路的TRNG，主要是利用混沌的参数敏感性和长期不可预测性等特性来产生真随机数序列。常见的混沌TRNG熵源有：分段线性映射混沌、时空混沌、忆阻器混沌、多维映射混沌等[8]。布尔混沌是由美国杜克大学ZHANG et al在自治布尔网络中发现的新型混沌[9]。与前述混沌熵源相比，其具有信号高幅值(≥1 V)、大带宽(-10 dB带宽可达数GHz)等优点，在发展高速TRNG方面具有突出优势[10]。

本文设计了一种基于布尔混沌的TRNG芯片，其真随机数最高输出速率可达100 Mbps.芯片设计采用中芯国际SMIC 0.35 μm 3.3 V CMOS标准工艺，核心电路面积0.02 mm2.针对所设计的芯片版图进行了参数提取及后端仿真，并对仿真产生的真随机数序列进行了香农熵、二维点阵图分析以及ENT测试，结果表明所产生的真随机序列具备良好的随机统计特性。

1 TRNG芯片设计

TRNG设计原理如图1所示，主要由2部分构成：熵源和熵提取电路。

图1 基于自治布尔网络的TRNGFig.1 True random number generator based on Autonomous Boolean network

熵源是一个自治布尔网络振荡器，它由18个自治节点组成，其中0号节点是一个两输入异或非门(XNOR)，而1-17节点则分别为两输入异或门(XOR).振荡器中每个节点的输入均是来自于相邻节点的输出。

熵提取电路是一个同步布尔网络，它由4个D触发器和2个二输入XOR门组合而成，其主要作用是：1) D触发器在时钟信号控制下对熵源(0，6，12节点)输出的混沌信号进行采样、量化，产生不可预测的“0”，“1”二进制真随机数序列；2) 利用2个XOR门组成的异或链电路消除真随机数中存在的偏置(即“0”和“1”数量不相等的现象)，实现高质量真随机数的持续稳定输出。

在CMOS工艺下，TRNG中的逻辑器件(XOR和XNOR)可以通过多种电路结构来实现，常见方法有静态电路实现、动态电路实现、伪NMOS电路实现以及传输门电路实现。相比其他三种方式，传输门电路的显著特点是只需要较少的晶体管就可以实现所需逻辑功能，有利于降低TRNG芯片的总体功耗；因此，本文使用传输门电路来构建XOR门和XNOR门。设计过程如下：首先，选择沟道宽度为0.35 μm的NMOS管和PMOS管，将2个MOS管的源极与漏极并联以构成传输门；其次，利用传输门分别构成异或门和异或非门[11]。所设计的传输门和异或门结构如图2(a)，(b)所示，而异或非门是在异或门基础上级联一个非门实现。TRNG整体设计如图2(c)所示，仅使用逻辑门、触发器等数字器件组成，具有结构简单、鲁棒性强等优点。

2 TRNG芯片仿真测试与随机性分析

2.1 TRNG芯片仿真测试

使用Cadence软件的Spectres工具对所设计的TRNG芯片进行了仿真测试。芯片时钟频率设置为100 MHz，电源电压3.3V ±10 %。自治布尔网络(从0号节点输出)产生的信号时序、频谱如图3(a)，(b)所示，信号呈现无规则连续振荡，幅值约3 V左右，其频谱为连续谱，-10 dB带宽约780 MHz，具有超宽带信号特性。进一步分析了无规则振荡信号的最大李雅普诺夫指数和自相关特性，如图3(c)，(d)所示。最大李雅普诺夫指数具体计算步骤如下：

1) 采集一段20 μs的振荡器输出信号V(t)，并通过和阈值Vcc比较将其转换成布尔变量x(t)∈{0,1}：当V(t)Vcc/2时，x(t)=1；其中，Vcc为电源电压；

2) 计算布尔距离函数d(s)：

图2 (a) 传输门；(b) 异或门；(c) TRNGFig.2 (a) Transfer gate; (b) XOR gate and (c) TRNG

(2)

式中：⊕代表逻辑异或运算，s∈[0,k*T0]为步长，ta和tb为任意两个时刻，对于给定的δ>0，T=T0，ta和tb的取值应使d(0)<δ成立；

3) 计算〈lnd(s)〉，〈·〉代表取平均；

4) 计算最大李雅普诺夫指数λab=(lnd(s)-lnd(0))/s.

选取T0=10 ns，δ=0.01，振荡器输出信号的最大李雅普诺夫指数λab=0.47 ns-1，如图3(d)所示；最大李雅普诺夫指数值为正，表明输出振荡信号为布尔混沌。其自相关曲线没有明显旁瓣，且半高全宽FWHM为0.68 ns，表明熵提取电路的速率还有进一步提升空间。

TRNG产生的真随机数序列如图4(a)所示，其输出码型为非归零码(NRZ)，幅值约3 V，序列中的最小码元宽度为10 ns，表示随机数输出速率达到了100 Mbps.随机序列对应二维点阵如图4(b)所示，由500×500=250 000个黑白像素点构成，其中白点和黑点分别对应随机序列中的“1” 码和“0”码，二维点阵图中没有明显的结构与花样，表明随机序列中“1” 码和“0”码具有良好的随机分布。

2.2 TRNG随机性分析

统计学测试是用于检验随机数质量的常规手段，常用的测试标准有NIST测试[12]、DIEHARD测试[13]、AIS31测试[14]以及ENT测试[15]等。其中，ENT测试具有样本需求量小的特点，常用于软件仿真等随机数生成效率较低的场合。仿真实验中，采集了TRNG芯片瞬态仿真产生的20 000 bit随机数样本，对其进行了ENT 5项测试，检测结果如表1所示，样本测试值均接近理想值，表明所产生的真随机数序列具有良好的随机统计特性。

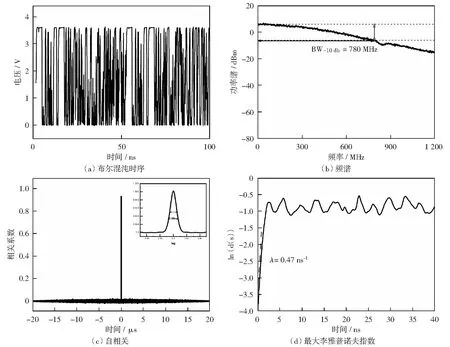
图3 自治布尔网络振荡器Fig.3 Autonomous Boolean network oscillator

图4 (a) 100 Mbps真随机数；(b) 500×500随机数二维点阵图Fig.4 (a) Real-time output random bit sequence at 100 Mbps; (b) Lattice diagram of of random data

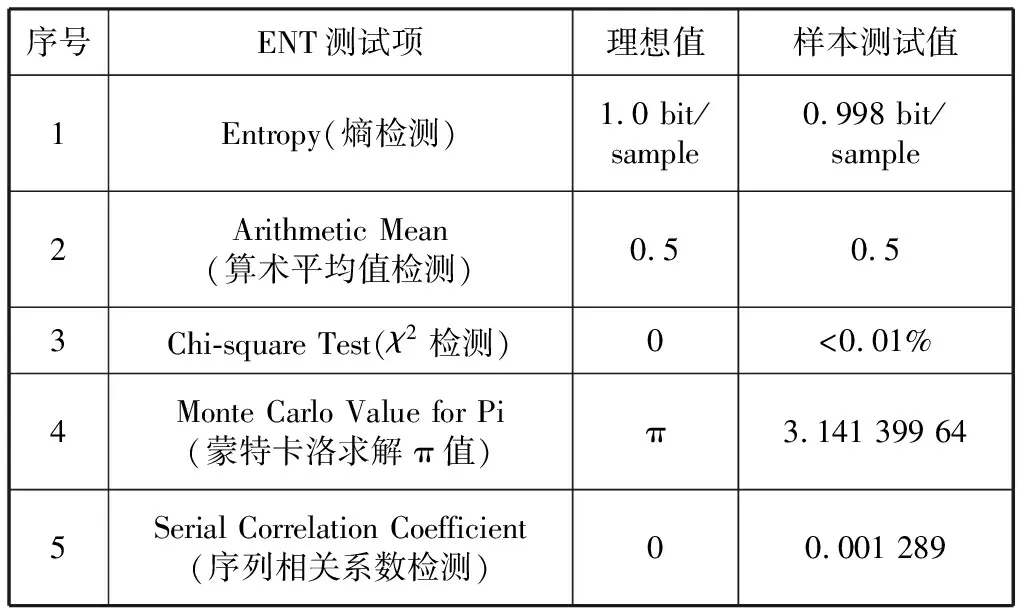
表1 ENT测试Table 1 ENT test

3 TRNG芯片版图设计

TRNG芯片全部采用数字单元实现，使用Cadence的Virtuoso完成版图实现。经过反复仿真调试后，根据中芯国际0.35 μm CMOS工艺进行了版图设计，如图5所示，其核心电路面积0.02 mm2(125 μm×163 μm)；目前，TRNG芯片正在中芯国际流片中。

图5 TRNG芯片版图Fig.5 TRNG chip layout

4 结论

本文采用SMIC 0.35 μm CMOS标准工艺，设计了一种以布尔混沌为熵源的真随机数发生器芯片，并详细分析了TRNG的熵源特性以及所产生真随机数的统计特性。结果表明该TRNG芯片仅使用较少数量的数字逻辑器件即可实现高速率、高质量的真随机数产生，具有结构简单、功耗低、鲁棒性好等优势，可广泛应用于密码系统、保密通信等领域的信息安全产品中。