深入探究,春暖花开
——一道江苏模拟解三角形的探究
☉江苏省张家港市沙洲中学 王春凤
三角形中的定值或最值问题是解三角形问题中的重点与难点之一,也是新课标大纲充分体现在“知识点交汇处”命题的一大阵地.此类问题往往设置巧妙,形式活泼多样,而且问题中知识的交汇比较多,有效提升了题目难度,从而使解决问题的思维方式多变,破解方法多种多样,一直是历年高考、自主招生、竞赛命题中的基本考点和热点之一.
一、问题呈现
【问题】(江苏省泰州市2019届高三上期末·14(泰州一调))在△ABC 中,已知,且sinAsinBsin(C-θ)=λsin2C,若为定值,则实数λ=______.
本题以△ABC 为问题背景,除了三角形的三内角外还引进了一个“外援角”,通过设置涉及含有参数λ 的四个角的三角关系式外,还借助三角形中没具体告知结果的三角关系式的定值问题,进而达到破解对应的参数值的目的.题中涉及角的参数较多,且三个内角之间又相互关联,参数与定值之间必然还存在某种关系,错综复杂.
二、多解剖析
思维角度1:(三角方程法)结合三角关系式的定值加以三角恒等变换,并引入定值参数,得到关于sin2C 的关系式,又结合条件,以及已知三角关系式的变形得到λsin2C的关系式,通过两对应关系式作商,得到关于tanC 的方程,利用条件得到相应参数的方程组,从而得以求解相应的参数值.

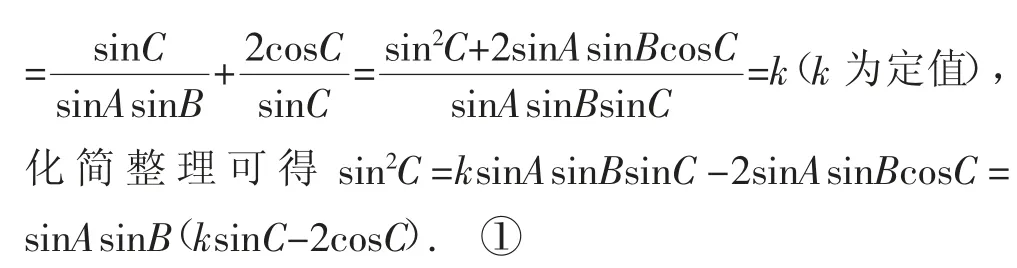
由sinAsinBsin(C-θ)=λsin2C,代入化简整理可得λsin2C=sinAsinB(sinCcosθ-cosCsinθ)=sinAsinBsinθ·(2sinC-cosC).②
而tanC的值是变化的,k、sinθ的值为定值,那么只能是解得,此时常数k=4.
思维角度2:(正弦定理法)结合三角关系式的定值加以三角恒等变换,以及正弦定理的应用,并引入定值参数,得到关于λc2的关系式,又利用已知三角关系式的变形,以及两角差正弦公式的应用得到λc2的关系式,通过比较两个三角关系式中的系数来求解相应的参数值即可.

而由sinAsinBsin(C-θ)=λsin2C,tanθ=(0<θ<π),可得
三、变式拓展
探究1:保留原问题的条件,转化求解目标,由原来求解实数λ的值改为求解定值k的值,从而得以变式.与原题难度相当,知识点一致,只是改变一个角度.
【变式1】在△ABC 中,已知,且sinAsinBsin(C-θ)=λsin2C,若为定值k,则实数k=______.
解析:结合以上问题的解析过程,可知常数k=4.
答案:4.
探究2:保留原问题的三角关系式,改变原来的已知条件进行角度转换,给出对应的定值但没给出定角θ的三角函数值,从而得以变式.与原题难度相当,知识点一致,也只是改变一个角度.
【变式2】在△ABC 中,已知sinAsinBsin(C-θ)=λsin2C,其中角θ 满足0<θ<π,且为定角,若,则实数λ=______.

探究3:在变式2 的基础上,由原来求解实数λ 的值改为求解定角θ 的正切值,从而得以变式.与变式2 难度相当,知识点一致,只是改变一个角度.
【变式3】在△ABC 中,已知定角θ 满足0<θ<π,且sinAsinBsin(C-θ)=λsin2C,若,则tanθ=______.
解析:结合以上变式2 的解析过程,可知
探究4:保留原问题的三角关系式,并直接给出原来的参数值,但没给出定角θ 的三角函数值,从而在明确三角关系式定值的基础上来确定该定值,从而得以变式.与原题难度相当,知识点一致,也只是改变一个角度.
【变式4】在△ABC 中,已知定角θ 满足0<θ<π,且sinAsinBsin(C-θ)=,若为定值k(k 为正数),则实数k=______.

四、规律总结
其实,探究解三角形中的相关参数、三角关系式的取值范围、最值及定值问题等,可以有效发现三角形中的边、角等知识之间的内在联系与变化规律,从而加强对相关内容的有效综合与合理转化,进而加以正确地理解与掌握相关的知识与破解方法,有助于数学解题能力与应用能力的提高,真正提升数学能力,拓展数学素养.

