加强目标意识 培养解题素养

☉江苏省苏州市西安交通大学苏州附属中学 梁 超

解题最怕没有思路，尤其在考场上，没有合理的思路，既会导致宝贵时间的流失，又会增加考生的心理负担.对大部分题目而言，解题需要分析条件和目标，学生往往重视条件转化，却忽视对目标的分析.解析几何作为江苏高考的重点考查内容，所占分值比较大，最能反应出考生“想”与“算”相结合的综合能力，笔者选取了三道较为典型的解析几何题，谈谈在解题过程中加强目标意识的重要性.

类型一、目标明确

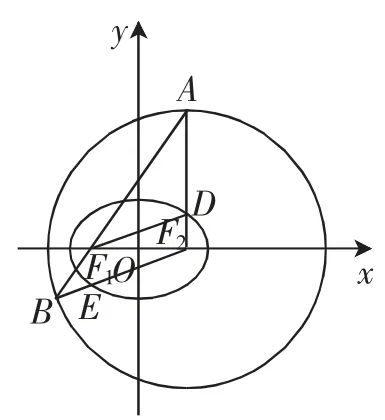
图1

例1（2019 年江苏卷第17题）如图1，在平面直角坐标系xOy中，椭圆C：=1（a＞b＞0）的焦点为F1（-1，0），F2（1，0）.过F2作x 轴的垂线l，在x 轴的上方，l与圆F2：（x-1）2+y2=4a2交于点A，与椭圆C交于点D.连接AF1并延长交圆F2于点B，连接BF2交椭圆C 于点E，连接DF1.已知

（1）求椭圆C 的标准方程；（2）求点E 的坐标.

思路分析：第（1）问的目标是求椭圆的标准方程，也就是要确定a，b的值.根据题意知c=1，结合椭圆中的天然关系a2=b2+c2，即有a2=b2+1 ①，我们再找到一个关于a，b的关系式，就可联立方程组解出a，b，这时需要落实到条件DF1=上.在直角三角形DF1F2中，由DF22=DF12-F1F22得.从而点D 的坐标为，代入椭圆方程得②，联立①②解出b2=3，a2=4.故椭圆C 的标准方程为=1.第（2）问的目标是求点E的坐标，我们自然地想求出直线BF2的方程，与椭圆方程联立后即可解出点E 的坐标.因为点F2是已知的，所以只需求出点B 的坐标.又知点B 是直线AF1与圆F2的交点，且点A和点F1是确定的，进而直线AF1是确定的，与圆F2联立即可求出点B，最后得到点E 的坐标为，具体过程从略.

反思总结：本题分值为14 分，属于稍有难度的中档题.我们通过分析目标，回溯到题干条件，两个问题分别利用方程思想、数形结合思想，即可将求解本题的脉络梳理清楚.虽然这种方法未必是最简便的，但整体思路是比较自然的，是大部分学生可以掌握的方法.解题素养的基本要求是迅速、准确、清楚、简练.解题的迅速性是指方法合理，在尽量短的时间内完成正确的解答.尤其在争分夺秒的高考考场上，若能迅速合理地找出解题思路，对于稳定心态、建立信心会有非常大的帮助.

解析几何题常作为江苏高考的中档题出现，做好解析几何题是冲刺高分的必要条件.上述例1 的题干条件还是比较多的，图形乍一眼看上去也略显复杂，但只要沉着审题、明确目标，理清目标与条件的关系，细心计算，本题完全可以争取拿满分.下面我们再研究两个例子，当面对题目的目标比较模糊，即目标与条件的关系不是很清晰，或者目标可实现的途径多样化时，我们该如何寻找思路？

类型二、目标模糊

例2（2013 年江苏卷第13 题）在平面直角坐标系xOy 中，设定点A（a，a），P 是函数图像上的一动点.若点P，A 之间的最短距离为，则满足条件的实数a 的所有值为______.

思路分析：本题的表层目标是求a 的值，但通过什么途径求，需要考生自己去挖掘.本题的一大误区是对图形认识不到位，部分考生想当然地将点P 固定为直线y=x 和曲线的交点（1，1），然后令PA2=2（a-1）2=8，解出错误答案a=-1 或3.

本题要实现从条件到目标的过渡，中间有一段模糊的距离，突破口在于研究“点P，A 之间的最短距离为.首先根据点P 所在曲线的特点，可设点，其中x＞0.从而，展开得PA2=x2-2ax+a2++a2.观察展开式的特点，整理可得PA2=）+2a2.此时不难发现，整体换元，令t=x+，则PA2就是关于t 的二次函数f（t）=t2-2at+2a2-2，并且f（t）的定义域为［2，+∞），对称轴为t=a，f（t）的最小值为8.问题就转化成熟悉的“抛物线动轴定区间问题”，分两种情形：a≤2和a＞2，对应的最小值为f（2）=8和f（a）=8，最终解得a=-1 或

反思总结：本题作为填空题的倒数第二题，综合性较强，具有一定的难度.考生在解此题时主要会遇到三类障碍：一是由于解题经验不足或对难题的畏惧心理导致毫无头绪，直接放弃解答；二是主观上带有较大的盲目性，感性地取定点P（1，1）；三是不会对式子PA2=（xa）2+进行化简转化.数学解题不仅是智力活动，也是心理活动，除了平时要积累通性通法，考场上更要善于构建目标与条件之间的桥梁，才能在规定时间内准确地实现思维活动.

类型三、目标可实现途径多样

例3（2018 年江苏卷第18题）如图2，在平面直角坐标系xOy中，椭圆C 过点，焦点，圆O的直径为F1F2.

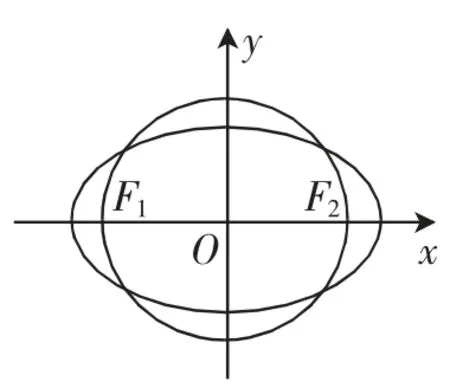
图2

（1）求椭圆C 及圆O 的方程；

（2）设直线l 与圆O 相切于第一象限内的点P.

①若直线l与椭圆C有且只有一个公共点，求点P的坐标；

②直线l 与椭圆C 交于A，B 两点.若△OAB 的面积为，求直线l 的方程.

思路分析：容易求出本题第（1）问的答案，椭圆C：+y2=1 及圆O：x2+y2=3.第（2）问分两问，目标分别是求点P 的坐标和直线l 的方程，可以说目标还是比较明确的.考生审题之后，不难想到两个切入点：一是设点P（s，t），其中s＞0，t＞0，二是设直线l：y=kx+m（k＜0，m＞0），这就是目标可实现的途径是多样的.实际上无论是设点还是设直线，都是引入了两个未知数，所以我们都需要找两组关系，一组是大前提——直线l与圆O相切.如果是设点，需要先表示出直线，结合点P在圆O 上，即s2+t2=3，从而；如果是设直线方程，直线与圆相切可转化成圆心到直线的距离等于半径，当然也是直线与圆联立方程后，判别式Δ=0.

我们再来寻找另一组关系，对（2）中的①，将直线与椭圆方程联立后，由判别式Δ=0即得到另一个关系；对（2）中的②，先根据直线l 与圆O 相切，可将条件△OAB的面积转化成，所以另一个关系就是直线与椭圆联立后表示出的弦长AB.两种思路都能求得结果，即点，直线l：

反思总结：本题分值为16 分，题目易懂，几乎没有审题障碍，但问题具有复杂性，对于大部分考生而言，想要设点或设直线的目标意识还是比较清晰的.考场上最忌三心两意，当我们选定一种方法时，首先大致判断这个方法的可行性与合理性，然后便是沉着冷静地计算出来.本题“算”难于“想”，要求教师平时在教学过程中敢于让学生花时间算，教师带领学生一起算，克服对复杂计算的畏惧心理.

我们在解题时，需要将条件和目标结合起来看，构建条件和目标的有效联系路径，找到解题方法，进而思考方法是否可以优化.加强解题的目标意识不应局限于解析几何，同样适用于其他类型的题目.牢记解题目标意识，可有助于寻找解题的切入点，从而有效解决问题.在数学课程改革不断发展的过程中，数学核心素养的研究备受关注.新课程标准把以学生发展为本，落实立德树人的根本任务，培养提高学生的数学核心素养作为课程宗旨.培养数学核心素养的主要实现途径是培养数学解题素养，本文着重分析的目标意识只是解题素养的一个侧面，更多丰富的内容需要广大教师与学生共同研究创造.