探析数学思想在圆锥曲线问题中的应用
☉湖北省通山县第一中学 黄崇楹
虽数学题目变幻无穷,但数学思想方法相对不变.在圆锥曲线与方程这一部分内容中,运用相关数学思想进行解题,往往会收到出其不意的效果,以下联系几则实例进行剖析,以期对学生解题能有一定的启发.
一、数形结合思想
数形结合在求解圆锥曲线问题中主要体现在以下两个方面:一是通过“数”的精准性呈现“形”的某一属性;二是通过“形”的几何特性来呈现“数”之间的某一种关系.
例1已知圆的曲线方程M:,是一定点,在圆M 上有一动点P,点Q 和G分别在NP、MP 上,且满足,请尝试求点G 的轨迹方程.
解析:如图1,由,,得Q 为NP 的中点且GQ⊥PN,所以GQ为NP的中垂线.因此,从而因此,点G 的轨迹是长半轴长a=3,焦点为M、N的椭圆.故点G的轨迹方程是=1(y≠0).
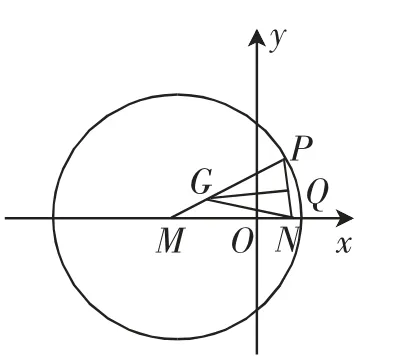
图1
点评:因本题条件繁多,假设通过转移法(或相关点法)求解点G 的轨迹方程,相对过程较为繁杂,且易出现一些错误,借助数形结合的思想进行处理,显而易见,直观简洁,事半功倍.
二、函数与方程思想
曲线的方程和方程的曲线有着天然的联系,曲线方程也可适当变形,变成函数.曲线和方程,方程和函数,三者之间的合理转化,便可将有关曲线问题“演绎”成二元二次方程组的问题、一元二次方程根与系数的关系问题、一元二次函数的最值问题等.
例2已知椭圆(a>b>0)的长轴长为4,右顶点为A,在椭圆上存在一点P,使OP⊥PA,求短轴长的取值范围.

点评:将b2用x0的函数来表示,然后,由0<x0<2 可以求得该函数的值域,函数与方程思想体现得淋漓尽致.另外,x0也可以表示成b2的函数,于是原问题就变成了一个关于b2的不等式,再求之.我们还可利用方程③的根的分布:一个根为2,另一个根位于区间(0,2)内,将其转化为根的分布问题也可让问题轻松获解.总之,方程及函数思想方法是解决圆锥曲线相关问题的一条有效路径.
三、分类讨论思想
在圆锥曲线问题中,常常会出现第三个量,即参数,采用分类讨论的策略是一条有效的路径.分类讨论,并非无章可循,有时按圆锥曲线的类型分类,有时按联立方程后方程的解的情形分类,但无论是哪种分类,必须缜密严谨做到有理有据、不重不漏.
例3当m 变化时,讨论方程mx2+(2-m)y2=1 表示曲线的形状.
解析:(1)当m<0时,方程表示焦点在y轴上的双曲线;
(4)当m=1 时,方程表示圆x2+y2=1;
点评:数学解题,应以概念、公式、定理、法则等为准则,而这些数学中的要素往往相互制约,牵一发而动全身,所以必须分类讨论.本题由于m 取不同的值会导致曲线的类型有异,所以必须将其全面讨论,虽然略显烦琐,但体现了数学的严密性.
四、化归思想
化归,其实就是等价转化,将要解决的新问题转化为已经解决的老问题.如何转化,我们必须对问题进行全面分析,将它与已经学习的知识相联系,方程向图形转化、动点向不动点转化、实际问题通过建模向数学问题转化……总而言之,转化就是化新为旧,化生为熟,化繁为简,化未知为已知,化出数学解题新天地.
例4已知椭圆C 的方程是,试确定m 的取值范围,使得对直线l:y=4x+m,椭圆C 上有不同的两点P、Q 关于该直线对称.
解法1:设椭圆C 上关于直线l 对称的两点为P(x1,y1),Q(x2,y2),其所在直线方程为,代入椭圆方程3x2+4y2=12,整理得13x2-8bx+16b2-48=0.

解法2:设PQ 的中点坐标为M(x0,y0),由解法1 知消去y0,把代入可得,所以x0=-m.
由于中点M的位置介于P,Q之间,所以必有不等关系(x1-x0)(x2-x0)<0,由此可得.经验证,当.适合条件的P、Q 存在,所以.故所求m的取值范围为
点评:解法1体现了解析几何问题常用的对称思想,数形结合是根本;解法2 体现了解析几何问题常用的不等式思想,建立方程组是关键.从两种不同的方法中可以看出,思考问题的角度不同,会得到不同的方法,两法难易不同,各有千秋,每一种方法都体现了转化与化归的数学思想.
总之,数学思想能使学生从本质上认识数学知识与方法,是学生形成良好认识的结构纽带,也是学生将知识转化成为能力与素养的桥梁,因此,在日常数学活动中,学生务必要高度重视数学思想方法的习得.

