思维如此活跃，椭圆如此巧妙——2019年全国卷Ⅰ解几题

☉山东省淄博实验中学 刘海峰

椭圆作为解析几何中的基本曲线，可以从解析几何角度切入，还可以从平面几何角度切入，其涉及解析几何知识、平面几何知识、平面向量知识、解三角形知识，以及三角函数、函数、不等式等相关知识，是新课标大纲中充分体现在“知识点交汇处”命题的一大主阵地.由于其变化多端，形式多样，创新点多，难度适中，而且破解的思维方式多样，切入点灵活，成为历年高考、自主招生、各类竞赛命题中的基本考点和热点之一.

一、真题在线

【高考真题】（2019年全国卷Ⅰ理10；文12）已知椭圆C的焦点F1（-1，0），F2（1，0），过F2的直线与C交于A，B两点.若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为（ ）.

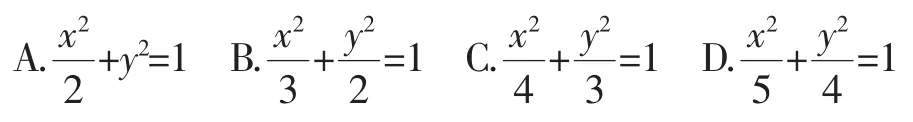
本题给出椭圆的焦点坐标，利用焦点弦的比例关系及相关线段的长度关系来确定焦点弦的准确信息，进而求解椭圆的标准方程.通过题目条件，把对应线段的长度关系加以合理转化，借助相应的知识与相关的方法加以破解.

二、一题多解

思维角度1.解三角形法

结合椭圆的相关知识，利用其中所构成的三角形的边与角的关系，结合三角形中的余弦定理加以过渡与转化，进而达到综合应用的目的.

方法1：（余弦定理法1）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m.

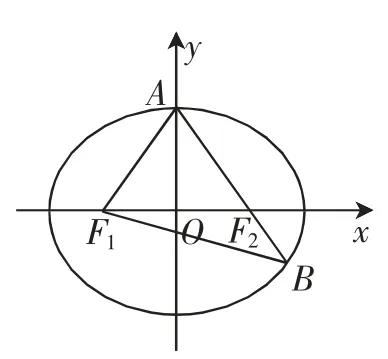
图1

在△AF1B 中，由余弦定理可得cos ∠F1AB=

在△AF1F2中，由余弦定理可得4=4m2+4m2-2×2m×2m×，解得m=

答案：B.

方法2：（余弦定理法2）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m.

在△AF1B 中，由余弦定理可得cos ∠F1BA=

在△BF1F2中，由余弦定理可得4=9m2+m2-2×3m×m×，解得m=.

答案：B.

方法3：（余弦定理法3）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m.

设∠AF2F1=θ，在△AF1F2和△BF1F2中，由余弦定理得，整理可得，解得m=

答案：B.

思维角度2.平面几何法

结合椭圆的相关知识，利用其中所构成的三角形的边与角的关系，通过三角形相似、角平分线定理等平面几何知识加以过渡与转化，进而达到综合应用的目的.

方法4：（相似比例法）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m=|AF2|，可知A（0，b）（不失一般性，取A为上顶点）.

所以b2=a2-c2=2.所以椭圆C的方程为

答案：B.

方法5：（角平分线性质法）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m=|AF2|，可知A（0，b）（不失一般性，取A为上顶点）.

如图2，取AF1的中点H，连接BH交x轴于点E，则知BH⊥AF1，且BH平分∠ABF1.

结合角平分线性质可知|EF1|∶|EF2|=|BF1|∶|BF2|=3∶1，可得

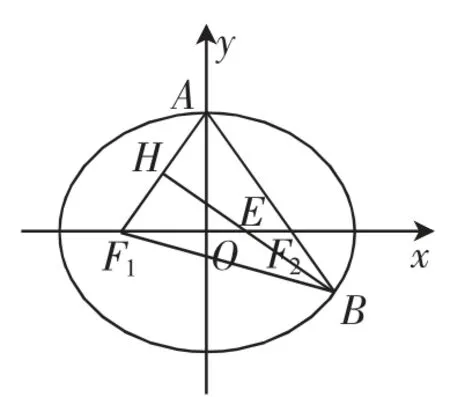
图2

在△AF1O中，cos∠AF1O=，在△HF1E中，cos∠HF1E=，则有，解得a2=3.

所以b2=a2-c2=2.所以椭圆C的方程为=1.

答案：B.

思维角度3.椭圆第二定义法

方法6：（椭圆第二定义+同位角法）由椭圆C的焦点F1（-1，0），F2（1，0），可知c=1.

由于|AF2|=2|F2B|，|AB|=|BF1|，所以设|BF2|=m，则|AF2|=2m，|BF1|=|AB|=3m.

根据椭圆的定义可知2a=|BF1|+|BF2|=3m+m=4m，得a=2m.

所以|AF1|=2a-|AF2|=4m-2m=2m=|AF2|，可知A（0，b）（不失一般性，取A为上顶点）.

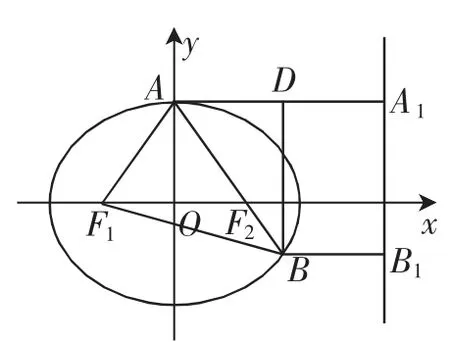
图3

由于cos ∠AF2O=，cos ∠BAD=，可得，解得a2=3.

所以b2=a2-c2=2.所以椭圆C的方程为

答案：B.

三、规律总结

在处理圆锥曲线的相关问题中，要合理分析题目条件，转化为代数法（解析几何、解三角形等）或几何法（平面几何等）来处理，巧妙转化，合理应用，争取达到“小题小做，小题巧做”，有助于数学解题能力与应用能力的提高，真正提升综合能力，拓展数学素养.