黏弹性结构精细化频域动力分析方法
盖盼盼,徐赵东,吕令毅,戴军
(东南大学土木工程学院,江苏南京,211189)
黏弹性材料作为一种高效的阻尼材料,已被广泛应用于航空航天、土木工程、机械工程等领域中的振动控制[1-2]。含有黏弹性材料或者具有黏弹性特性的结构被称为黏弹性结构,其动力特性常受加载频率和环境温度的影响,表现为典型的频率/温度依赖性[2-3],需用复模量模型[4-5]、分数导数模型[6-8]或积分型模型[9-10]进行本构表达,其中积分型模型是基础模型,其余模型均为该模型的近似或无限逼近[11],所以,基于黏滞阻尼系统的实模态叠加法无法准确获得黏弹性结构的频域响应。国内外学者针对黏弹性结构动力响应的求解方法进行了大量研究,其中应用最为广泛的是模态应变能法和状态空间法,前者仅在一定程度考虑黏弹性材料储能模量和损耗因子的频率依赖性,并且对于高阶模态参数的估计不准确;后者虽然精度较高,但涉及复数计算,且计算量较大。MENON等[12]将黏弹性结构的特征方程转化为多项式方程,并在状态空间中建立了等价一阶系统,简化了分析过程。DE LIMA 等[13]提出了采用子结构装配技术获得黏弹性结构的频响函数,并可以方便地与有限元模型结合,但准确频响函数的获得对实验设计的要求过于严苛。LÁZARO 等[14]采用非阻尼特征向量和具有振荡特性的复特征向量将黏弹性系统近似为等效黏滞模型,该方法兼备了计算效率和精度,但对应用于非比例阻尼水平较高的系统时应谨慎考虑这种近似对精度的影响。石银明等[15]引入黏弹性材料的微振子模型建立黏弹性结构的动力方程,并采用鲁棒性降阶技术缩减方程的维数及提高计算效率。李创第等[16]引入黏弹性材料的广义麦克斯韦模型建立黏弹性结构的扩阶方程,并基于复模态理论获得了结构地震响应的解析解。具有强频率依赖性的黏弹性结构动力响应的精确性和效率仍存在较难协调的问题,本文作者将经典黏弹性本构和传统实模态叠加法结合起来,并采用分步迭代,避免求解含有复数的高阶特征方程以提高计算效率;将黏弹性结构频域响应的求解简化为多个进行频率依赖性函数修正的单自由度黏弹性结构频域响应的叠加,以提高计算精度。
1 黏弹性结构的动力方程
黏弹性材料由于特殊的微观结构而兼具黏性液体和弹性固体的特性,在动力作用下应变滞后于应力,从而产生阻尼效应。应力应变关系常用松弛函数表示,其中广义麦克斯韦模型应用广泛,力学模型如图1所示,表达方式如下:
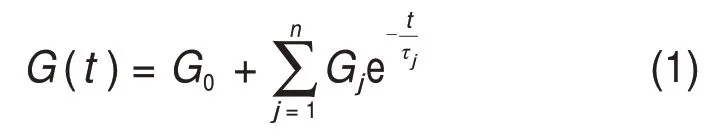
式(1)可以在频域内改写为复模量的形式:
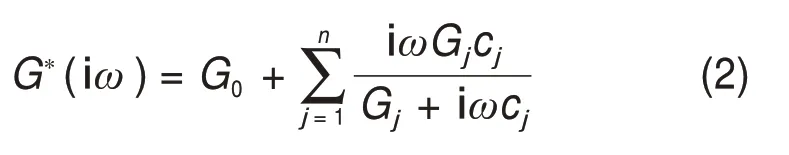
式 中:G∗为剪切复模量;G0,Gj,cj和τj(τj=cj Gj为广义麦克斯韦模型的参数,通过实验数据拟合确定;i = -1,为虚数单位。

图1 广义麦克斯韦模型Fig.1 Generalized Maxwell model
当结构中含有黏弹性材料或具有黏弹性效应,结构的复刚度可写成与式(2)相同的形式:

式中:K0为结构中的线弹性刚度项;K1和K2分别为结构黏弹性部分的储能刚度和耗能刚度。若黏弹性结构中的恢复力以复刚度的形式表示,则黏弹性结构动力方程的频域形式如下:

式中:M为黏弹性结构的质量矩阵;F为施加于结构上的动力荷载向量;u为位移矩阵。对于黏弹性材料,常用损耗因子η= imag(G∗)/real(G∗)表征材料的耗能能力,本文仿效黏弹性材料损耗因子的定义,定义黏弹性结构的损耗因子矩阵如下:

式中:K=K0+K1定义为结构的整体刚度。将式(5)代入式(4),可获得黏弹性结构动力方程的一般频域形式:
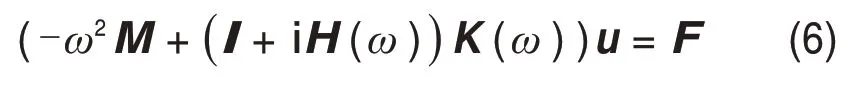
2 特征方程求解
从式(4)略去动力荷载向量,可获得黏弹性结构的特征方程:
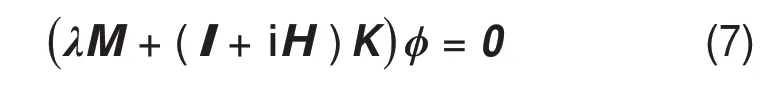
式中:λ和ϕ分别为特征方程的特征值和特征向量;λj= -ωj2(1 + iηj);ωj为第j阶模态频率;ηj为第j阶模态的损耗因子,与黏滞阻尼结构中的阻尼比ξj的关系为ξj=ηjωj/(2ω)。从式(7)可以看出;K∗为复数矩阵且具有明显的频率依赖性,致使黏弹性结构的特征方程求解计算量大。为了避免复数运算,忽略方程中的耗能刚度,获得无阻尼黏弹性结构的特征方程:
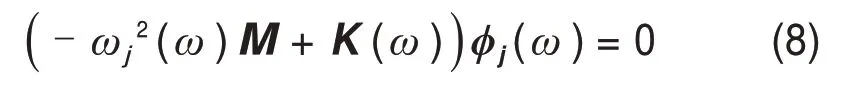
需注意的是,当ωj(ω)=ω时,获得的模态频率、振型和损耗因子才是考虑刚度矩阵频率依赖性的模态频率振型和损耗因子。为适用于实模态叠加法,本文对迭代法[17]进行分步处理来计算黏弹性结构的模态参数,目的在于避免复数运算,依次求得模态频率和模态损耗因子。首先假设K(ω)=K(0),求得的第一阶模态频率作为初始迭代频率ω(0)1,进而更换刚度矩阵K(ω)=K(ω(0)1),重新求解特征方程(8),将获得新第一阶模态频率代入如下收敛准则进行比较:

式(9)中,ε通常取较小值作为迭代法的收敛值。依此类推,可以获得N个感兴趣的模态频率与振型。整个收敛过程可以用下式表达:
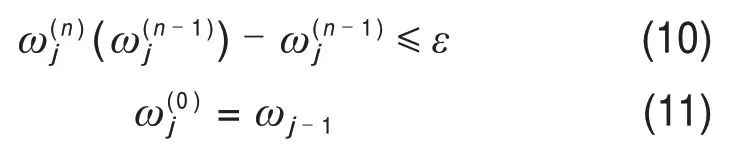
模态损耗因子的计算还需要考虑耗能刚度K2的频率依赖性,可以按照下式计算:
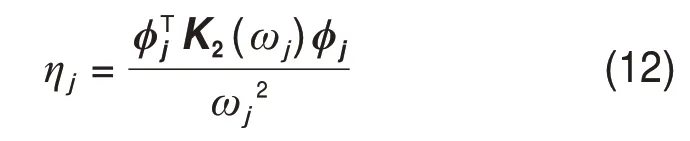
振型ϕj为归一化振型,满足ϕTj ϕj= 1。上述求解黏弹性结构特征方程的方法既考虑了复刚度的频率依赖性,又避免了复数的运算,数值算例结果表明,各阶模态参数的计算只需迭代3~4次即可满足,计算量小,物理意义明确。
3 改进的实模态叠加法
根据实模态叠加法的思想,结构的动力响应可由N个非阻尼振型的叠加表示,引入u=Φq,并将计算得到的模态参数带入方程(6),忽略矩阵的非对角元素,可获得N个独立的单自由度结构的动力方程:
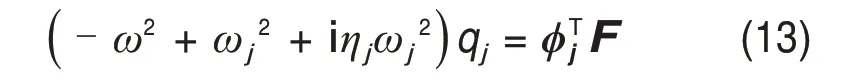
式中:qj为黏弹性结构的广义坐标。根据方程(13),具有频率依赖性的结构动力响应可以简化为N个无频率依赖性的结构动力响应叠加。
但是,在实际迭代计算过程中,当迭代当前模态参数时,已完成迭代的上一阶模态参数仍会发生变化,对于强频率依赖性的黏弹性结构,这样的变化更加明显。这是由于尽管经过前面求解所得模态参数考虑了黏弹性结构的频率依赖性,但简化后的单自由度结构源于原始黏弹性结构,本质上简化后的N个单自由度结构仍具有黏弹性,所以,方程(13)中的模态参数ωj和ηj在单自由度结构中仍然需要考虑频率依赖性。故需对传统的实模态叠加法进行改进。
在迭代求解黏弹性结构模态参数过程中,选取其中的2N×N模态参数信息。
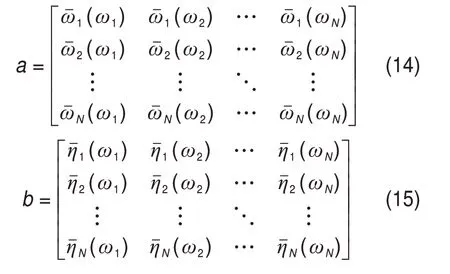
式中:(ωj)和(ωj)分别为最后1 次迭代计算所得第j阶模态时第i阶模态的模态频率和损耗因子。这里采用多项式拟合来表征单自由度结构ωj和ηj的频率依赖性,数学表达形式如下:

式中:fj(…)和gj(…)分别为用括号内数据拟合ωj和ηj的多项式。将式(16)和(17)代入方程(13),qj的表达方式如下:

则第i个自由度的频域响应为:

式中:ui,vi和ai分别为第i个自由度的位移、速度和加速度的频域响应。
4 算例
为了验证本文所提计算黏弹性结构频域响应的简化算法,以1个六自由度黏弹性结构作为计算对象进行算例分析,其力学模型如图2所示。图2中,k为黏弹性结构中不随加载频率变化的固定储能刚度,取为105N/m;质量m取为1 t,g为黏弹性结构中随加载频率变化的复刚度,采用广义麦克斯韦模型表征,参数取值见文献[18],分别考虑了弱频率依赖性和强频率依赖性2类情况。图3所示为2类情况下,黏弹性结构整体复刚度随加载频率变化的情况。从图3可知:2 类储能刚度均随着加载频率的增加而增加,且强频率依赖性结构表现出更加显著的储能刚度频率依赖性;2类损耗因子(耗能刚度/储能刚度)随着频率的增大而先增大后减小,由于强频率依赖性结构所含的黏弹性比例较高,所以,展现出更加显著的耗能能力。
采用分步迭代法求解黏弹性结构的特征方程,图4所示为2 类黏弹性结构的模态频率的具体信息。从图4可知:2 类结构的模态频率均表现出与储能刚度相似的频率依赖性,其中强频率依赖性结构的模态频率依赖性水平显著,加载频率从1阶增大到6 阶,对应的各阶约模态频率提高了10%。值得指出的是,这些数据将通过多项式拟合来表征各单自由度黏弹性结构的模态频率依赖性,采用3 次多项式即可取得满意的结果。图5所示为2类黏弹性结构的模态损耗因子的具体信息。从图5可知:2类模态损耗因子均表现出了与前述损耗因子(耗能刚度/储能刚度)相似的频率依赖性,且强频率依赖性的黏弹性结构具有更大的模态损耗因子。与图4不同的是,由于本文表征模态耗能能力的指标定义为复刚度理论中的模态损耗因子而非模态阻尼比,致使每阶模态都具有相同数值和频率依赖性水平的模态损耗因子,也就是在进行多项式拟合时,各阶模态共用1个代数式。

图2 黏弹性结构的力学模型Fig.2 Mechnical model of viscoelastic structure

图3 黏弹性结构复刚度的频率依赖性水平Fig.3 Frequency dependence level of complex stiffness
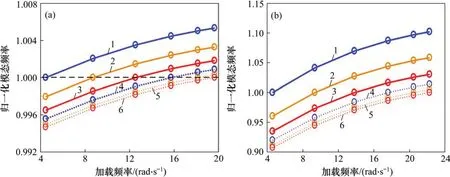
图4 黏弹性结构模态频率的频率依赖性水平Fig.4 Frequency dependence level of modal frequency
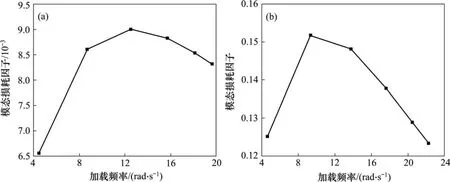
图5 黏弹性结构模态损耗因子的频率依赖性水平Fig.5 Frequency dependence level of modal loss factor
将拟合多项式代入式(18),将各模态响应叠加即获得黏弹性结构的频域响应。这里以名义传递函数mω2o|H(2,4)|替代频域响应以利于检查各阶模态的响应,其中ω2o=k/m。图6所示为2 类黏弹性结构的名义传递函数曲线,这里采用了模态应变能法、迭代法作为对比方法,精确解通过直接对不同频率下的矩阵进行求逆获得。从图6可以看出:对于弱频率依赖性的黏弹性结构,3类方法给出的曲线和精确解十分吻合,模态应变能法在高阶模态非共振频率下的精度略有降低。但对于强频率依赖性的黏弹性结构,模态应变能法给出的高阶响应精度较低;迭代法虽然给出各阶模态共振频率下满意的结果,但是在非共振频率下精度降低,这不利于黏弹性结构在具有复杂频谱的激励下响应的精确预测;而本文提出方法给出的曲线与精确解高度吻合,说明该方法适用于强频率依赖性黏弹性结构的频域响应预测。
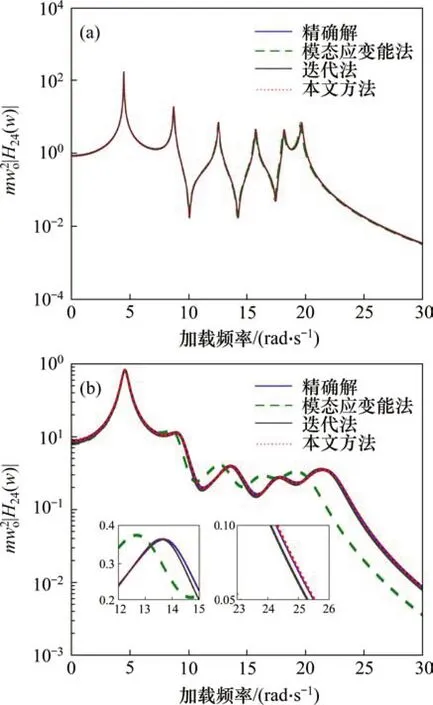
图6 黏弹性结构频域响应Fig.6 Frequency response of viscoelastic structure
5 结论
1)本文基于实模态叠加法,引入麦克斯韦本构,建立了黏弹性结构的动力学方程;对特征方程进行分步迭代求解,依次获取各阶模态的模态频率、振型和损耗因子;将黏弹性结构简化为N个独立的单自由度黏弹性结构,采用多项式拟合修正各阶模态参数的频率依赖性水平,最终求得黏弹性结构的频域响应。
2)所提方法将经典黏弹性本构和传统实模态叠加法结合起来,并采用分步迭代,避免了求解含有复数的高阶特征方程。
3) 考虑模态分解后所得到的N个单自由度结构仍保留的黏弹性特性,采用多项式拟合表征各阶模态参数的频率依赖性水平;与模态应变能法和迭代法相比,本文提出的基于实模态叠加的简化方法可以很好地计算出具有强频率依赖性黏弹性结构的频域响应,精度高且物理意义明确。

