干湿循环作用对水泥改良泥质板岩土路基动力响应影响的模型试验

朱自强，刘雨,2，陈俊桦

(1.中南大学地球科学与信息物理学院，湖南长沙，410012；2.湖南省有色地质勘查研究院，湖南长沙，410015；3.桂林电子科技大学建筑与交通工程学院，广西桂林，541004)

化学改良土在路基工程中应用很广，工程中最常见的化学改良土为石灰改良土和水泥改良土。通常水泥改良土的力学稳定性比石灰改良土的强。水泥改良土或石灰改良土的强度和刚度高，抗水软化性强，承载性良好。但文献[1-7]的研究表明，即使经过石灰或者水泥改良，土的静动强度、静动弹性模量、内摩擦角和黏聚力等仍然会在干湿循环作用下产生一定程度的衰减。地下水位上升和下降、降雨和蒸发等干湿交替是化学改良土路基产生不均匀沉降和破裂等现象的重要原因之一。干湿循环作用降低改良土的力学性质，从而影响改良土路基的动力响应，给道路交通运行带来安全隐患。研究干湿循环对化学改良土路基动力响应的影响可以为化学改良公路、铁路等化学改良道路工程的安全稳定性评估提供参考。路基动力响应研究方法主要包括数值模拟、现场试验和模型试验[8-9]。数值模拟一般是根据实际工况建立路基动力计算模型，通过数值计算得到动应力、动应变和振动速度等物理量的响应规律[10-12]。现场试验需要在路基土内埋设动土压力盒、动位移计和振动速度传感器等测量元器件，当路面车辆经过时，通过测量元件采集测点的响应信号，从而获得路基动力响应规律[13-15]。数值模拟可以节省研究成本和方便控制试验条件，但由于土的工程性质均较复杂，数值模拟结果往往与现场实测结果之间有较大差距。现场试验具有研究成本高、试验条件难控制等缺点，例如，现场路基干湿循环就很难得到控制，但现场试验结果能够比较真实地反映实际车辆荷载作用下的路基动力响应特点。路基模型试验通常是根据实际工程建立路基比例模型，对路基面进行动力加载时，通过埋设在路基体内的元器件测得动应力、动应变和振动速度等[16-17]。据尺寸不同，路基比例模型包括足尺比例模型和非足尺比例模型；据材料不同，路基比例模型分为同材料模型和相似材料模型。路基比例模型动力响应与实际路基的动力响应有相似性。当路基模型的材料和尺寸均与实际相同时，模型试验结果的可靠度最高[16-17]。目前，人们对干湿循环条件下改良土路基动力响应的研究很少。与现场试验相比，模型试验可以模拟干湿循环作用和灵活控制加载试验条件，例如，为模拟路基干湿循环，可以在路基模型周边修建可蓄排水的水池。与数值模拟相比，模型试验结果更接近现场实测结果[1]，可见足尺比例路基模型试验是开展干湿循环条件下化学改良土路基动力响应研究的最优方法。由于含绿泥石、高岭石和蒙脱石等为亲水矿物成分，所以，泥质板岩土的水稳性差，表现为泥质板岩土颗粒遇水易发生崩解，从而导致泥质板岩土体发生软化以及干湿作用下出现干缩和湿胀等现象。干湿变化对泥质板岩土的力学性质有重要影响[1,18-19]，从安全角度考虑，对于高等级公路或者高速铁路的路基，一般采用化学改良后的泥质板岩土进行填筑[19-20]。为揭示干湿循环对化学改良泥质板岩路基动力响应的影响规律，本文作者以水泥改良泥质板岩土筑的公路路基为研究对象，在实验室内设计和建立干湿循环条件下足尺比例泥质板岩路基的动力加载与测试系统。通过开展干湿循环条件下的路基动力响应测试，测得动应力、动应变和累积变形等响应量，分析干湿循环作用对这些响应量的影响。

1 干湿循环条件下的路基动力试验设计

1.1 路基模型设计

1.1.1 泥质板岩土样

土样取自湖南岳阳市区，为褐黄色泥质板岩土。土中主要含白云母、石英、绿泥石、高岭石和钠长石等矿物成分，其中，绿泥石和高岭石为吸水矿物成分。土样的颗粒粒径小于40 mm，不均匀系数和曲率系数分别为28.7 和7.4。未改良土的级配曲线见图1。根据GB/T 50145—2007 “土的工程分类标准”，泥质板岩土样命名为级配不良的含细粒土砾。

1.1.2 路基模型的几何尺寸

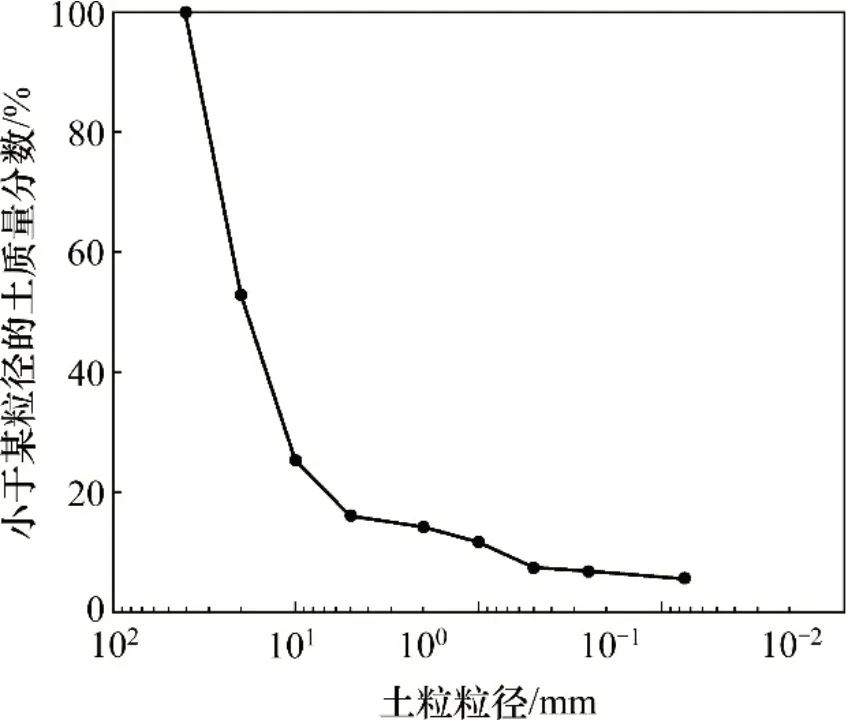
图1 泥质板岩土样的级配曲线Fig.1 Gradation curve of argillaceous-slate soil sample

根据JTG D30—2015“公路路基设计规范”设计足尺比例的公路路基模型。路基模型高度为2.30 m，长度为3.00 m。路基顶部宽为3.75 m，底部宽度为9.75 m。路基边坡坡度为1.0:1.5。路基模型从上而下分为路面结构和路基本体。其中，路面结构是厚度为0.30 m的混凝土板，板面长×宽为3.75 cm×3.00 cm，混凝土强度等级为C30。路基本体填料为水泥改良后的泥质板岩土，高度为2.00 m。路基模型横断面示意图见图2。

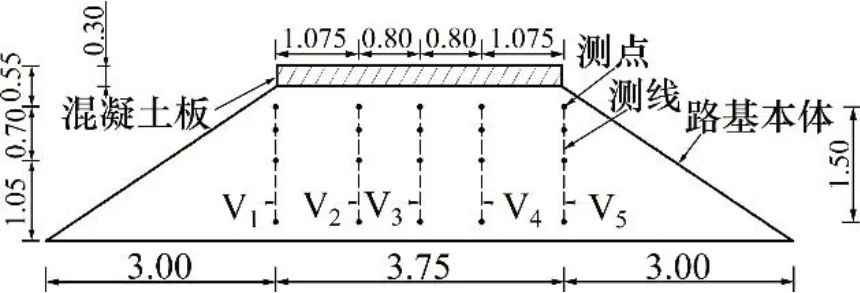
图2 路基动力试验模型横断面Fig.2 Diagram of cross section of dynamic test model of subgrade

1.1.3 泥质板岩土改良及填筑工艺

以图1所示的级配曲线制作泥质板岩土样，然后在制作好的土样中掺入普通硅酸盐水泥P.O32.5对土进行化学改良。根据文献[13-15]的研究成果，当土中水泥质量分数超过4%时，泥质板岩改良土符合高速公路或者高速铁路路基填筑的要求。对于本文试验，水泥改良土中掺入的水泥质量分数为5%，土中含水率为15%，土干密度为2.0 g/cm3。当养护龄期达到28 d 时，改良土的无侧限抗压强度约为1.0 MPa。按照JTGF 10—2006“公路路基施工技术规范”的要求填筑路基。采用湖南理工学院结构实验室内的路基模型进行实验。

1.2 路基动力加载和动力响应测量系统设计

1.2.1 路基动力加载系统和加载条件设计

路基动力加载通过湖南理工学院结构实验室内的静动力加载系统进行，该系统主要由法定平台、反力钢架、FCS011 电液伺服协调加载控制系统和作动器等组成。系统可施加力为-300～300 kN，加载频率为0～20 Hz。加载模式包括力加载和位移加载，动态加载波形包括矩形波、三角波和谐波等。对于路基动力加载试验，作动器作用在路基顶部的混凝土面板上，作用面为矩形，矩形长×宽为0.30 m×0.40 m。

公路面上作用的车辆移动荷载通常为复杂的随机循环荷载，就目前国内外的技术水平而言，要使路基比例模型动力试验的动力加载完全与实际情况相符很难实现。车辆移动荷载可以假设为一系列简谐振动叠加而成的周期性动荷载，车辆移动荷载对路面的作用可以简化为单个车轮对路面的集中作用[21]。根据该假设，路基动力加载条件可以简化，动力加载可以采用1个作动器进行，且加载波形可以选用形式简单的谐波。对于本文试验，通过1个作动器在路面混凝土板上施加正弦波动力开展路基动力加载。作动器中轴线经过混凝土面板板面的中心，路基动力加载示意图见图3。

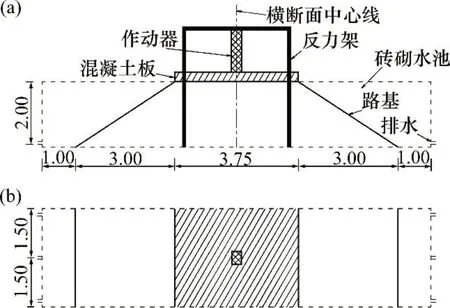
图3 路基动力加载和干湿循环控制系统示意图Fig.3 Diagram of dynamic loading and drying-wettingcontrol on subgrade

正弦波动力的表达式为[9]

式中：F为作动器施加的动力；P为动力幅值；f为加载频率；t为时间；φ为初始相位。

单次试验中加载作用的总时间为

式中：tend为加载作用的总时间；Nend为动力加载的总循环次数。

1.2.2 路基动力响应测量系统设计

路基动力响应测线布置在包含作动器中轴线的路基横断面上，如图2所示。图2中，测线沿竖向布置，共有5条测线，从左至右，各测线依次记为V1，V2，V3(在横断面中心线上)，V4和V5。V1和V5及V2和V4分别关于V3对称，V1(或V5)与V3的距离为1.875 m，V2(或V4)与V3的距离为0.800 m。每条测线上均有4个测点。设测点与混凝土板顶部之间的距离为测点深度，记为h。对于任意1 条测线上的测点，从路面往下，测点深度h依次为0.55，0.85，1.25 和2.05 m。考虑到对称性的影响，除了V3同时布置动土压力盒、动应变计和位移计外，V1和V2只布置动土压力盒，V4和V5只布置动应变计。动土压力盒与动应变计分别测量动应力和动应变。采用位移计测量累积变形。路基动力响应试验一般主要研究竖向物理量的动力响应，因此，在试验中，动应力数据由测线V1，V2和V3采集，动应变数据由测线V3，V4和V5采集，累积变形由测线V3采集。测得的动力响应物理量均为竖向的物理量。

1.3 路基干湿循环设计

土的干湿循环过程包括吸水和失水。由于影响这一过程的因素很多，如温度、土的内部结构和矿物成分等，故目前国内外学者对土干湿循环控制标准的认识尚未达成一致。对于室内试验，控制土干湿循环的主要方法为自然风干、烘干、自然吸水和反压饱等，干湿循环周期按天(d)或者小时(h)度量[1-8]。文献[1]认为，由于土中孔隙较大，粗粒土容易吸水与失水，因此，提出了按天计算的干湿循环试验标准，即将试样浸泡水中使其自然吸水，吸水1 d后使试样自然风干，风干时间为1 d，此过程为1 次干湿循环。本文试验的路基填土属于水泥改良泥质板岩粗粒土，因此，试验采用文献[1]中的干湿循环控制标准。在路基周边修筑砖砌水池，并对水池进行防渗处理。水池可蓄排水，从而可以用来模拟路基干湿循环。水池几何尺寸见图3。图3中，水池高度为2.00 m，水池底板长度和宽度分别为11.75 m 和3.00 m。路基的1次干湿循环试验过程为：首先对水池进行蓄水，蓄水高度1.80 m，使浸泡在水中的路基自然吸水；当路基浸泡水中1 d后，水池排水；排水完成后，将路基自然风干，风干时间为1 d。

1.4 干湿循环条件下动力响应测试方案

1)由于当水泥改良土的龄期达到28 d 时其强度才逐渐趋于稳定，因此，当改良土路基龄期为28 d时对路基开展干湿循环试验。干湿循环次数记为M，共开展15次干湿循环。

2)每当路基完成1次干湿循环后，对路基测量1次循环动力加载和相应的动力响应。循环动力加载函数见式(1)，加载参数为：P=25 kN，f=4 Hz，φ=0°，Nend=40 000次，tend=10 000 s。

2 试验结果及分析

2.1 干湿循环对动应力响应的影响

设竖向最大动应力、竖向最大动应变和竖向累积变形分别为σmax，εmax和w，它们为路基动力响应特征量。本文通过分析它们与干湿循环次数之间的关系以揭示干湿循环作用对动力响应的影响。

2.1.1 干湿循环作用对动应力的影响

图4和图5所示分别为V2和V3测线上各测点的σmax首先与M之间的关系。从图4和图5可看出：对于同一测点，随着M增加，σmax不断减小且减小到一定程度后几乎不再发生变化。例如，图5中V3测线上深度h=0.55 m的测点，随着M从0次增加到8 次，σmax由42.3 kPa 减 小 至31.8 kPa，减 少10.5 kPa，随后，当M从8 次增加到15 次时，σmax由31.8 kPa 减少至28.6 kPa，减少3.2 kPa。在M从0 次增加至15 次的过程中，σmax虽然不断减少，但减小幅度逐渐趋近于0 kPa，σmax-M曲线也趋近水平。这表明干湿循环对路基动应力响应有一定影响，干湿循环作用能使竖向动应力减小，但这种减小作用是有限的，随着干湿循环次数增加而逐渐失效。2.1.2 动应力沿路基深度方向传播衰减规律及干湿循环对动应力衰减的影响

图4 测线V2竖向最大动应力与干湿循环次数之间的关系Fig.4 Relationship between vertical maximum dynamic stress and dry-wetting cycle times of line V2

图5 测线V3竖向最大动应力与干湿循环次数之间的关系Fig.5 Relationship between vertical maximum dynamic stress and dry-wetting cycle times of line V3

图6所示为V3测线上各测点的σmax与路基深度h之间的关系曲线。从图6可以看出：竖向最大动应力随着测点深度或者传播距离的增加而衰减。为分析干湿循环作用对动应力传播衰减的影响，利用下式对σmax和h之间的关系进行拟合：

式中：k为竖向最大动应力传播的场地系数；α为最大竖向动应力的衰减系数。

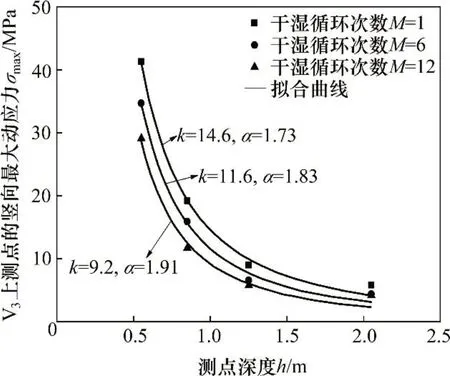
图6 测线V3竖向最大动应力与测点深度之间的关系Fig.6 Relationship between vertical maximum dynamic stress and depth of testing point of line V3

图6中，拟合曲线的相关系数为0.982～0.998，拟合关系良好。α和M之间的关系见图7。从图7可以看出：对于测线V1，V2和V3，随着M增加，α均逐渐增加，但增加幅度逐渐减小，使得α逐渐趋于稳定值。例如，对于测线V2，当M从0次逐渐增加至8次时，α从1.17逐渐增加到1.35，增加0.18；当M继续从8次逐渐增加至15次时，α从1.35增加至1.40，增加0.05。在M从0次增加至15次的过程中，α虽然增加，但增加幅度不断减小，最终α-M曲线趋近水平。干湿循环作用对路基竖向动力应传播衰减有一定影响，随着干湿循环次数增加，竖向最大动应力的衰减增加并最终逐渐趋于稳定。

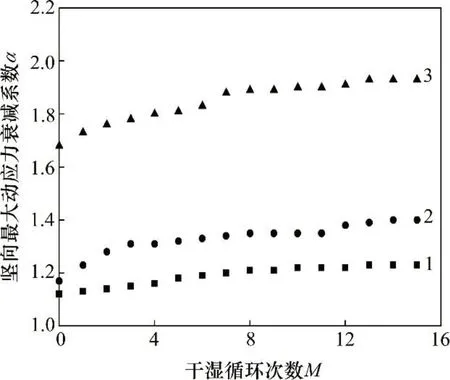
图7 竖向最大动应力的衰减系数与干湿循环次数之间的关系Fig.7 Relationship between attenuation of vertical maximum dynamic stress and dry-wetting cycle times

2.2 干湿循环对动应变响应的影响

2.2.1 干湿循环作用对动应变的影响

图8和图9所示分别为V3和V4测线上各测点的εmax与M之间的关系。从图8和图9可以看出：对于同一测点，随着M增加，εmax不断增大且增大到一定程度后几乎不再发生变化。例如，对于图8中V3测线上h=0.85 m 的测点，随着M从0 次增加到9 次，εmax从188.6με增加至233.7με，减少45.1με；当M从9 次继续增加到15 次时，εmax由233.7με增加至236.3με，增加2.6με。在M从0次增加至15次的过程中，εmax虽然不断增加，但增加幅度逐渐减小并趋近于0，εmax-M曲线也趋近水平。因此，与竖向最大动应力一样，竖向最大动应变响应也随干湿循环次数而发生变化并最终趋于稳定。不同的是，随着干湿循环次数的增加，竖向最大动应变逐渐增加，而竖向最大动应力则相反。

图8 测线V3竖向最大动应变与干湿循环次数之间的关系Fig.8 Relationship between vertical maximum dynamic strain and dry-wetting cycle times of line V3

图9 测线V4竖向最大动应变与干湿循环次数之间的关系Fig.9 Relationship between vertical maximum dynamic strain and dry-wetting cycle times of line V4

2.2.2 动应变沿路基深度方向传播衰减规律及干湿循环对动应变衰减的影响

图10所示为V3测线上各测点的竖向最大动应变和测点深度之间的关系曲线。从图10可以看出εmax随着h增加而衰减。利用下式对εmax和h之间的关系进行拟合：

式中：l为竖向最大动应变传播的场地系数；β为竖向最大动应变的衰减系数。

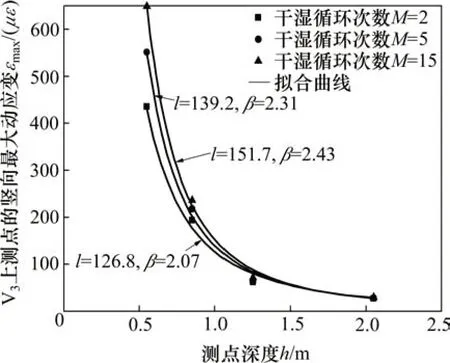
图10 测线V3竖向最大动应力与测点深度之间的关系Fig.10 Relationship between vertical maximum dynamic strain and depth of testing point of line V3

图10中，拟合曲线相关系数为0.994～0.998，拟合关系良好。竖向最大动应变的衰减系数和干湿循环次数之间的关系见图11。从图11可见：随着M增加，β逐渐增加，但增加幅度逐渐减小，β逐渐趋于稳定值。例如，对于测线V3，当M从0次逐渐增加至8 次时，β从1.96 逐渐增加到2.38，增加了0.42；当M从8 次逐渐增加至15 次时，β从2.38增加至2.43，增加了0.05。在M从0增加至15的过程中，β虽然增加，但增加幅度不断减小，最终β-M曲线趋近水平。与竖向最大动应力的衰减一样，随着干湿循环次数增加，竖向最大动应变的衰减增加并最终逐渐趋于稳定，即竖向最大动应变的衰减在一定程度上受到干湿循环作用的影响。

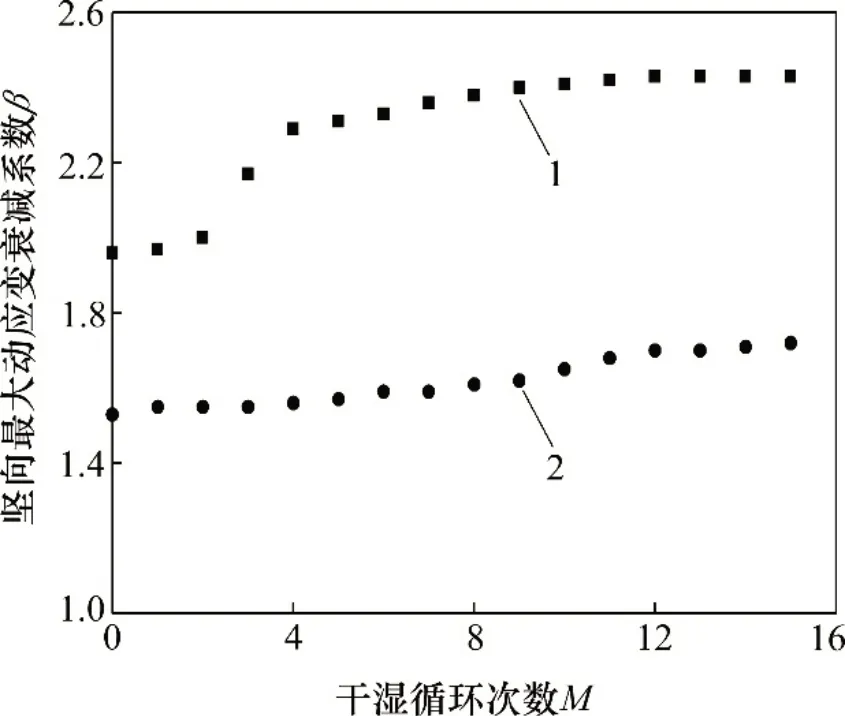
图11 竖向最大动应变的衰减系数与干湿循环次数之间的关系Fig.11 Relationship between attenuation of vertical maximum dynamic strain and dry-wetting cycle times

2.3 干湿循环对累积变形的影响

根据弹塑性力学，动应变包括可逆的弹性应变和不可逆的塑性应变。累积变形属于不可逆变形。图12所示为累积变形w与干湿循环次数M之间的关系。从图12可以看出：测点深度h=0.55 m处的累积变形最大，当M=15 次时，w=2.5 mm；h=0.85 m 处的累积变形次之，当M=15 次时，w=1.4 mm；对于测点深度h=1.25 和2.05 m 的测点，累积变形为0 mm。这表明累积变形是在路基一定深度内产生的，超过了该临界深度，累积变形为0 mm。在本文试验条件下，该临界深度不小于1.25 m。在临界深度以上，测点深度越小，测得的累积变形越大。从图12还可以看出：在临界深度以上范围内，即当h≤1.25 m 时，随着干湿循环次数增加，测点的累积变形不断增加并逐渐趋于稳定，即干湿循环作用对路基动力累积变形有一定影响。与动应变一样，累积变形同样随深度增加而衰减。

图12 竖向累积变形与干湿循环次数之间的关系Fig.12 Relationship between vertical accumulative deformation and dry-wetting cycle times

2.4 干湿循环对路基动力响应影响原理

水泥改良后，泥质板岩土中形成了水泥凝胶胶结网络，这使得改良土由水泥胶结形成的网络骨架和凝胶包裹的土颗粒构成。由于水泥在改良土中所占质量分数仅为5%，水泥凝胶不可能完全包裹住全部土颗粒团，因而水泥凝胶与外界有交流，同时，胶结网络也不是均匀分布在土内，故水泥改良土的力学性质实际上由水泥胶结网络和土颗粒的性质决定。水泥胶结网络骨架的水稳性强，但胶结包裹的土颗粒团仍然保持原有的力学特性，水稳性差，因此，土颗粒团会发生干缩和湿胀等现象。干缩和湿胀变形必然会受到水泥胶结骨架的限制，当变形超过骨架的强度时，骨架产生开裂现象，其强度和刚度随着裂缝扩展而降低，即干湿循环作用使改良路基的弹性模量降低。

根据一维弹性平面纵波理论，材料的动弹性模量近似和波阻抗成正比[22-25]，故干湿循环导致水泥改良路基的波阻抗减小。路基顶面作用的振动波经过混凝土板传播到改良土路基的过程实际上可以看作入射应力波由波阻抗不变的混凝土板透射到波阻抗减小的路基土中。作用在混凝土板上的是入射波和反射波，作用在路基土上的是透射波。根据一维弹性平面纵波在2种介质物质的反射与透射理论，当入射应力波强度及入射波作用物体的波阻抗均不变时，透射波作用物体的波阻抗越小，透射波产生的应力越小，而产生的应变越大[25-27]。按照该理论，对于本文试验，加载动力不变相当于入射波应力强度不变，而入射波作用的混凝土板的波阻抗也没有发生变化。干湿循环次数增加导致路基的波阻抗减小，从而减小路基中透射波产生的动应力，增大透射波产生的动应变与累积变形，即干湿循环减小路基中的动应力(见图4和图5)，增大路基中的动应变(见图8和图9)和累积变形(见图12)。

影响固体材料中应力波随距离传播而衰减的因素很多，波阻抗就是其中的重要因素[28-29]。在入射应力波强度不变时，波阻抗越小，透射应力强度衰减越快[22-24]。对于本文试验，随着干湿循环次数增加，路基的波阻抗降低，因此，路基动力响应衰减随着干湿循环次数增加而增大，即动应力和动应变的衰减随干湿循环次数的增加而增大(分别见图7和图11)。

由于干湿循环作用对泥质板岩土的动弹性模量的影响是有限的[1]，即干湿循环对泥质板岩土的波阻抗的影响也是有限的，因此，动应力、动应变和累积变形等虽然会随干湿循环增加而发生变化，但最终会趋于稳定。

3 结论

1)干湿循环作用对路基竖向动应力和竖向动应变的响应均有一定影响，但对两者的影响存在异同点。在动力加载条件不变的情况下，随着干湿循环次数增加，竖向最大动应力逐渐减少并最终趋于稳定；而竖向最大动应变逐渐增加，最终也趋于稳定。

2)干湿循环作用对路基动力响应传播衰减有一定影响。沿路基深度方向，竖向最大动应力和竖向最大动应变均逐渐衰减。衰减系数均随着干湿循环次数的增加而增大，且增大到一定程度后趋于稳定。

3)累积变形在路基一定深度内产生。超过该临界深度，累积变形为0 mm，在该临界深度范围内，累积变形随深度的增加而减小。对于本文试验，该临界深度不小于1.25 m。随着干湿循环次数增加，累积变形不断增加并逐渐趋于稳定。

4)虽然干湿循环作用增大了路基的动力变形，对路基动力安全稳定性产生了不良影响，但随着干湿循环次数增加，这种影响逐渐减弱，因此，干湿循环作用对水泥改良泥质板岩土路基动力安全稳定性产生的不良影响有限。