一个解变分不等式问题的非单调Broyden-like算法
(武夷学院数学与计算机学院,福建 武夷山 354300)
1 预备知识
考虑变分不等式问题(简记VI(X,F))[1-5]:求向量x*∈X,使得对于任意的x∈X有:
(x-x*)TF(x*)≥0,
(1)
成立。 其中,向量函数F(x):Rn→Rn为连续可微函数。
2010年,Zhang、Liu等人提出了可行域[1]:X={x|Ax>b,x∈Rn,A∈Rm×n,b∈Rm}的VI(X,F),记D=AT,文中的VI(X,F)皆是该类VI(X,F),其KKT系统为:F(x)-Dy=0,yT(Ax-b)=0,y≥0,Ax-b≥0。记s=Ax-b,则有
F(x)-Dy=0,s=Ax-b,y≥0,s≥0,yTs=0。
(2)
采用Fischer-Burmeister(FB)函数[6-7]:
将式(2)等价转化为方程组问题,即
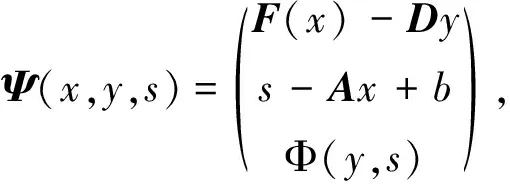
(3)
其中,

(4)
显然函数φFB(a,b)=0⟺a≥0,b≥0,ab=0,但是FB函数在点(0,0)处不可微,通过引入光滑参数μ>0,得到一个光滑FB函数:
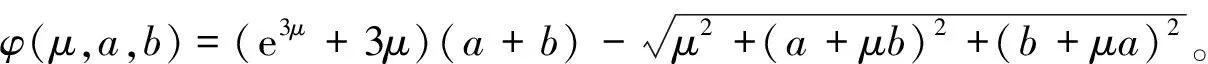
(5)
那么,φ(0,a,b)=φFB(a,b)。
令z=(μ,x,y,s)∈R++×Rn×Rm×Rm,
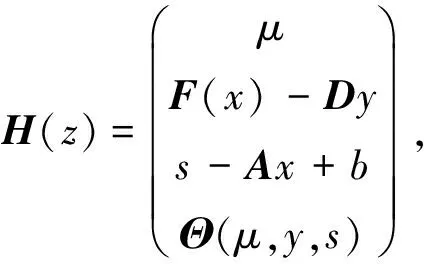
(6)
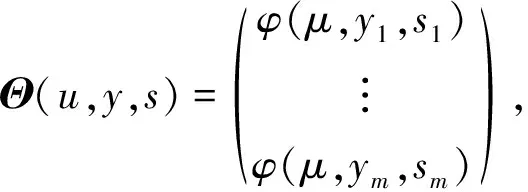
(7)
那么式(2)等价于以下方程组问题:
H(z)=0。
(8)
通过计算,得
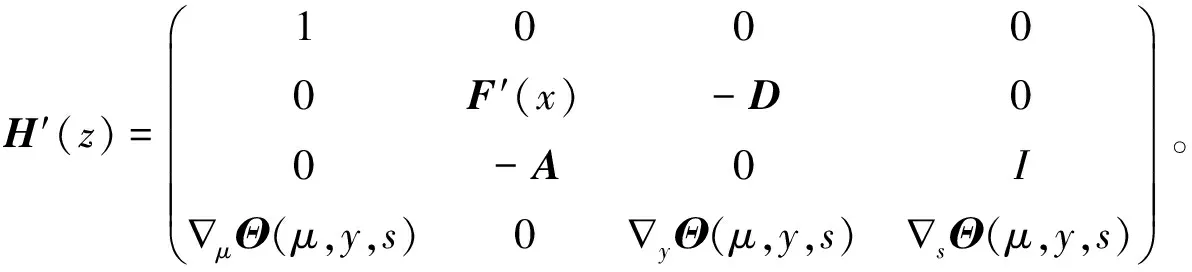
(9)
其中,
μΘ(μ,y,s)=vec{[φ(μ,yi,si)]′μ:i∈N},
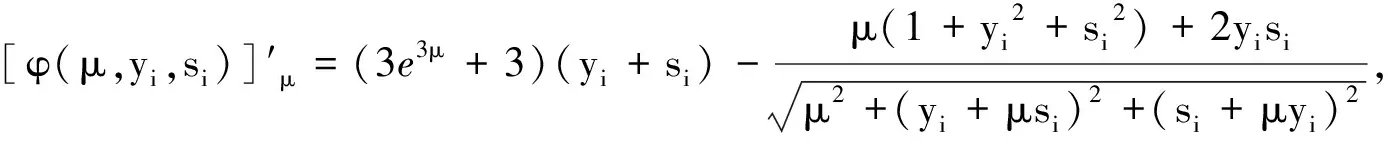
(10)
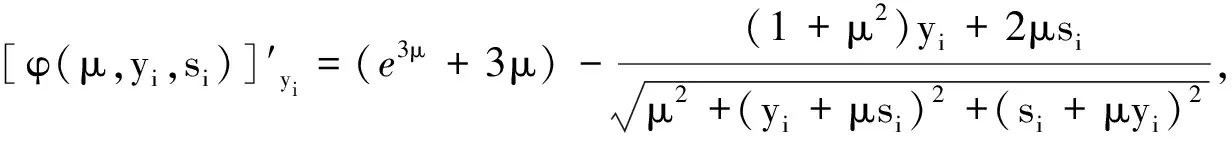
(11)
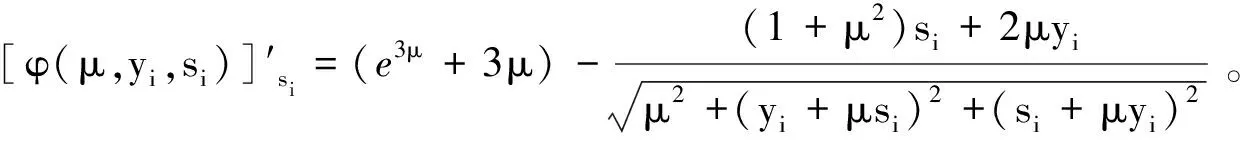
(12)
那么可得,对于任意的i=1,2,…,m,有
0≤[φ(μ,yi,si)]′yi≤e3μ+5μ,0≤[φ(μ,yi,si)]′si≤e3μ+5μ。
引理1设函数H(z)由式(6)定义,则下面结论成立。
1)对于任意的z∶=(μ,x,y,s)∈R++×Rn×Rm×Rm,函数H(z)是连续可微的;
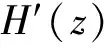
下文中的矩阵A均为列满秩矩阵。
2 非单调Broyden-like算法
本节建立了求解由式(8)定义的方程H(z)=0的非单调Broyden-like算法。 定义价值函数:
f(z)=||H(z)||。
(13)
显然,有f(z)=0⟺x是VI(X,F)的解。
下面给出算法的具体步骤。
算法1(解VI(X,F)的非单调Broyden-like算法)
步骤2 若f(zk)=0,算法结束;否则,计算
βk∶=β(zk)=γmin{1,f(zk)2},
(14)
并求解下列方程组:
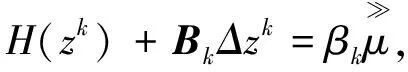
(15)
得向量组Δzk, 其中Bk为由式(9)定义的H(zk)的近似矩阵。
步骤3 若不等式
f(zk+Δzk)≤αf(zk)-σ||Δzk||2,
(16)
成立,令λk∶=1且转步骤5。
步骤4mk为使得下式成立的最小非负整数m,
f(zk+δmΔzk)≤Ck-σ1‖δmΔzk‖2-σ2δmf(zk),
(17)
则令λk=δmk,其中
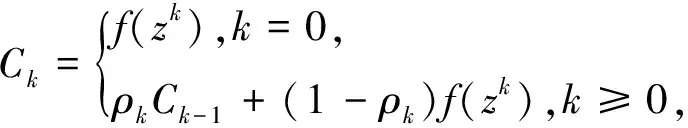
(18)
且ρk∈[ρmin,ρmax],转步骤5。
步骤5 令zk+1:=zk+λkΔzk。
步骤6 更新Bk得到Bk+1
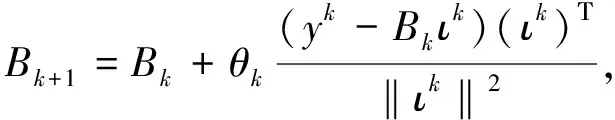
(19)
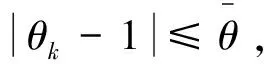
注:非单调线搜索式(17)由Gu和Mo在文献[8]首次给出,式(18)中若ρk=0,那么非单调线搜索转化为文献[9]中提出的单调线搜索。
引理2算法1是适定的。即对于所有的k≥0,必存在一个非负整数mk使得非单调线搜索式(17)成立。
证明 当λk→0+时,显然有f(zk)≤Ck。
由C0的定义,可知当k=0时结论成立。 假设f(zk)≤Ck,下面证明f(zk+1)≤Ck+1。 下面分两种情况进行讨论。
情况一 若式(16)成立,那么f(zk+Δzk)≤αf(zk)≤f(zk)≤Ck。
情况二 若算法1运行了式(17),那么f(zk+1)≤Ck-σ1||λkΔzk||2-σ2f(zk)≤Ck。
那么,可得式f(zk+1)≤Ck成立,结合式(18),可得
f(zk+1)-Ck+1=ρk+1(f(zk+1)-Ck)≤0。
(20)
综上可得,对于任意的k≥0有f(zk)≤Ck。 证毕。
由引理2,可得:
推论1 若序列{zk}由算法1迭代生成,那么对于任意的k≥0,有
f(zk)≤Ck。
(21)
引理3设H(·)以及β(·)分别由式(6)和式(14)定义,那么
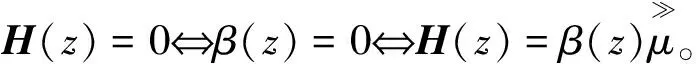
证明参见文献[10]引理5。
3 收敛性分析
本节讨论算法1的全局收敛性和局部超线性/二次收敛性。 为了分析算法1的收敛性,给出下述假设:
假设1
1)水平集Ω={z∈R++×Rn×Rm×Rm|f(z)≤f(z0)}有界;
2)矩阵H′(z)在集合Ω中是Lipschitz连续的,即存在常数l>0使得
||H′(z1)-H′(z2)||≤l||z1-z2||,∀z1,z2∈Ω;
3)对于任意的z∈Ω,矩阵H′(z)为非奇异矩阵。
引理4设序列{zk}由算法1迭代生成,那么序列{Ck}是非增单调的,且{zk}⊂Ω。
证明参见文献[10]引理6。
引理5若假设1成立,设序列{zk}为由算法1迭代生成的序列,那么
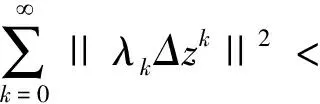
方便起见,定义
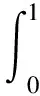
(22)
那么,有yk=Ak+1ιk,其中yk=H(zk+1)-H(zk)且ιk=λkΔzk。 由Bk+1的更新公式,有
(23)
更进一步,令
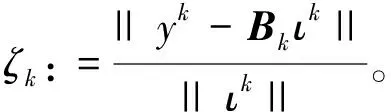
(24)
那么,
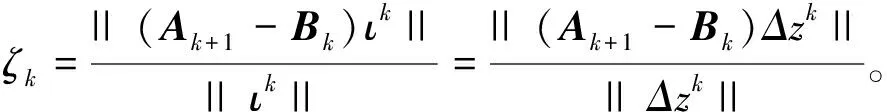
(25)
下面的引理来源于文献[11]的引理2.6。
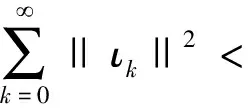
那么
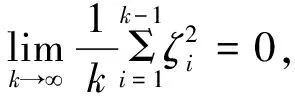
(26)
特别地,序列{ζk}的一个子列趋于0。 此外,若
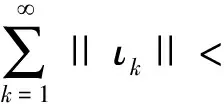
(27)
那么
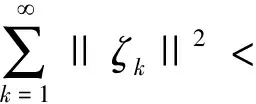
(28)
特别地,整个序列{ζk}收敛于0。
定理1若假设1成立,序列{zk}由算法1迭代生成,那么序列{zk}的任意聚点都是方程(8)的解。
证明由假设1和引理4,可知序列{zk}有界。 不失一般性,假设序列{zk}收敛于序列{zk}的聚点z*。 那么,可以得到z*满足等式f(z*)=0。 随后分两种情况进行讨论:
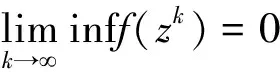
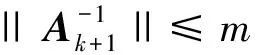
即对于所有充分大的k∈K,存在常数m1>0,有
||Δzk||≤m1f(zk),
(29)
成立。 不妨设序列{Δzk}k∈K收敛于Δz*=(Δμ*,Δx*,Δy*,Δs*),由式(25),可得||(Ak+1-Bk)Δzk||=ζk||Δzk||。 对于k∈K,令k→,可得BkΔzk→H′(z*)Δz*。 另一方面,对于k∈K,令等式(15)两边k→,可得
H(z*)+H′(z*)Δz*=β(z*)μ*。
(30)
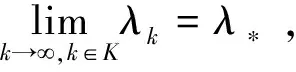
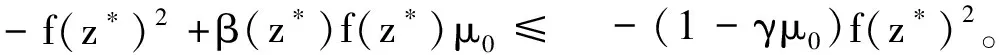
(31)
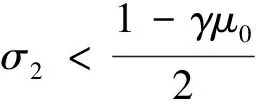
引理7[10]设函数F:Rn→Rn是局部Lipschitz函数,那么
1)类似于Clarke[12],函数F有广义雅克比 ∂F(x)。 且若函数F在点x处半光滑,则在点x沿着方向h∈Rn函数F的方向导数F′(x;h)存在。 另外,函数F在点x∈Rn处半光滑等价于其所有的分量函数在点x∈Rn处半光滑。
2)函数F在点x处半光滑,当且仅当对于所有的V∈∂F(x+h),h→0,有
||Vh-F′(x:h)||=o(||h||)。
另外,||F(x+h)-F(x)-F′(x:h)||=o(||h||)。
3)函数F在点x处强半光滑等价于对于所有的V∈∂F(x+h),h→0,有
||Vh-F′(x;h)||=O(||h||2)。
另外,||F(x+h)-F(x)-F′(x:h)||=O(||h||2)。
引理8[10]令函数H和函数Θ分别由式(6)和式(7)定义,那么
1)函数Θ是半光滑的。
2)函数H是局部Lipschitz和半光滑的,更进一步,若函数F′(x)Lipschitz连续,那么,函数H是强半光滑的。
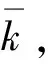
f(zk+Δzk)<αf(zk)-σ||Δzk||2,
(32)
成立。
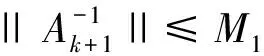
||Δzk||≤M2f(zk)。
(33)
成立。 由函数H的半光滑性,对于任意的充分逼近于z*的zk,存在正常数L1,使得
f(zk)=||H(zk)-H(z*)||≤L1||zk-z*||,
(34)
成立。 另一方面,由H′(z*)的非奇异性以及序列{zk}收敛于z*,存在常数L2>0,使得
f(zk)=||H(zk)-H(z*)||≥L2||zk-z*||,
(35)
成立。 由式(34)和式(35),有
o(||zk-z*||)=o(||H(zk)-H(z*)||)=o(||H(zk)||)。
(36)
由式(33)和式(34),可得
||Δzk||≤M2||H(zk)-H(z*)||≤M2L1||zk-z*||。
(37)
由式(15),得
(Ak+1-H′(zk))(zk-z*)+(Ak+1-Bk)Δzk-[H(zk)-H(z*)-H′(zk)(zk-z*)]。
那么,得
||zk+Δzk-z*||≤M1(ζkM2f(zk)+γμ0f(zk)2+o(||zk-z*||))≤
M1(ζkM2L1||zk-z*||+o(||zk-z*||))。
(38)
那么,当zk充分逼近于z*时,得
f(zk+Δzk)≤||H(zk+Δzk)-H(z*)||≤L1||zk+Δzk-z*||≤
M3ζk||zk-z*||+o(||zk-z*||)。
(39)
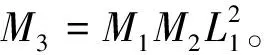
f(zk+Δzk)-αf(zk)+σ||Δzk||2≤M3ζk||zk-z*||+o(||zk-z*||)-αL2||zk-z*||+
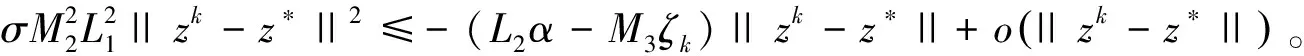
(40)
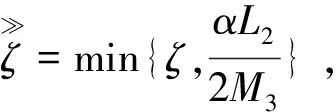
由此可得,当zk充分逼近于z*时,有λk=1满足式(31)。
下面分析算法1的局部超线性收敛性。
定理2若假设1成立,序列{zk}由算法1迭代生成,且z*为{zk}的聚点,那么,序列{zk}超线性收敛于z*,即||zk+1-z*||=o(||zk-z*||)。
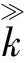
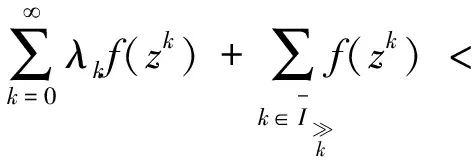
(41)
由式(35),得
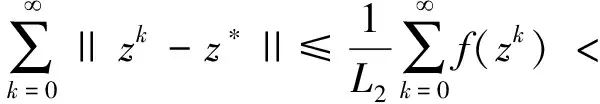
(42)
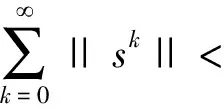
由引理6,可得,当k→时,ζk→0。
下面给出算法1的局部二次收敛性。
定理3设假设1成立,若所有的V∈∂H(z*)都是非奇异的,对于任意的x∈Rn函数F′(x)Lipschitz连续,那么,由算法1生成的序列{zk}二次收敛于VI(X,F)的解z*=(0,x*,y*,s*),即||zk+1-z*||=O(||zk-z*||2)。
证明类似于文献[13]的定理5.2。
4 结语
讨论了一类变分不等式问题,基于Fischer-Burmeister函数,建立了求解变分不等式问题的非单调Broyden-like算法,并证明的算法的全局收敛性以及局部超线性/二次收敛性。

