基于改进Shapley值法的供应链制造联盟利益分配研究

张 英，徐伊平，周兴建

(1.武汉理工大学 物流工程学院，湖北 武汉 430063；2.武汉纺织大学 管理学院，湖北 武汉 430200)

为了快速响应市场需求变化，供应链制造联盟成为企业变革的重要战略[1]。制造企业借助云平台组成临时联盟，通过制造企业间的多主体业务协同和制造资源与服务的集成与共享，为市场提供高效率、高质量、低成本的制造服务[2]。制造企业间形成联盟的目的在于实现多主体利益的最大化与合作共赢。合理的利益分配是上下游企业愿意参与制造联盟的根本动力，是实现高效协作的根本保障。因此，有必要探究供应链制造联盟主体间的合作关系以及与之相适应的利益分配机制。

国内外学者运用合作博弈理论对供应链利益分配问题开展了大量研究，合作博弈理论中Shapley值法[3]、核仁法[4]和谈判理论(或讨价还价法)[5]等是常用的方法。其中，Shapley值法是求解合作博弈利益分配的代表性方法，该方法简单实用，并且能根据研究对象的不同而不断完善修正。GAO等[6]针对可转移支付不确定的联盟博弈情形，在原Shapley值法的基础上提出了不确定Shapley值来解决不确定的联盟博弈利益分配问题；全春光等[7]利用Shapley值法解决因供给商管理库存合作而产生的利益分配问题，提出了一种供应商与两分销商均可接受的、稳定的成本分担方案。黄勇[8]针对猪肉供应链收益分配不均衡的现象，分别测算每个经济主体单独经营时的利润和各经济主体合作经营时的利润，基于Shapley值法，根据供应链各方对合作联盟的贡献程度，实现了成员间利益分配的协调；XU等[9]研究发现合作情形下的决策可以改善资源型供应链的收益，同时对原Shapley值法进行了修正，考虑了风险、生态和其他努力水平因素，形成了一个更为有效的收益分配机制；骆进仁等[10]指出Shapley值法在利润分配方面避免了非合作下调水公司一方主导的不利局面，并引入风险因素和投资因素修正因子，研究表明修正的Shapley值法可以使分配结果更加公平。

在云制造系统中，交易都要通过云服务平台处理，因此多数情况下云服务平台占据主导地位[11]，易造成非合作策略下一方主导而有损其他成员的不利局面。而且云制造模式具有“分散资源集中化、集中资源分散化”的特点，联盟主体间的交互更为频繁和复杂，因此合作过程中多主体的关系协调是云制造供应链联盟稳定发展的重要问题之一。但总体来看，已有研究尚未考虑到联盟主体间的协同性和激励效应对利益分配结果的影响，且将平台方纳入博弈过程的供应链利益分配研究较少。因此，笔者充分考虑制造联盟成员间的协同效应以及利益分配方式对于利益分配的激励作用，构建了客户奖金激励策略下云制造平台运营方与制造商协同合作的利益分配模型，并结合Stackelberg博弈模型和改进的Shapley值法对双方的合作利益进行了合理分配。

1 模型建立

1.1 问题描述与相关假设

制造商和云制造平台运营方愿意建立联盟的前提是解决好合作利益分配问题。因此，考虑由一个制造商和一个云制造平台运营方(以下简称平台方)构成的供应链制造联盟。

(1)假设客户方为了激励平台方提供优质、高效的制造资源和服务，会同平台方达成一种协议，即在给予平台方固定总价的基础上，还给予一定的奖金激励。于是，平台方所获利益p由两部分组成，即：

p=p1+λM(e1,e2)

(1)

式中：p1为客户给平台方的固定总价；e1，e2分别表示双方为提高服务质量、缩短制造时间而付出的努力程度；M(e1,e2)为平台方与制造商协同合作的产出函数，表示平台方与制造商协同合作后所表现出的制造资源质量的提高、制造时间的缩短等；λ为客户的奖金激励系数，0<λ<1,λ值的大小与产出函数的值正相关，即双方的协作产出越高，额外的奖金激励越多。

其中，α和1-α分别为平台方和制造商的努力程度对协同合作总产出的贡献权重，代表双方在协同合作中的相对重要程度，α与1-α由平台方与制造商的固有属性所决定，0<α<1；u为协同合作的产出系数，u>0；ei>0(i=1、2)。

(3)假设平台方为了激励优质制造商加入平台并与其建立良好的合作伙伴关系，会与其达成一种协议，即将客户所给予的奖金按线性分配规则进行利益分配，平台方与制造商的利益份额分别为β和1-β，因此双方的直接利益分别为：

ω1=p1+βλM(e1,e2)

(2)

ω2=p2+(1-β)λM(e1,e2)

(3)

其中，p2为平台方给予制造商的固定总价。此外，当制造商接入云平台时，需要支付给平台接入费用S，即接入成本，但是相较于不接入平台，自主寻找客户订单，将付出更大的代价C(C>S)，由此产生的节约成本为ω=C-S，亦即制造商入驻平台所带来的接入收益。同时，平台也将获得来自制造商的接入收益S，可见双方合作是互利双赢的。

(5)假设平台方和制造商是风险中性的，且以上信息对双方都是共同知识，不存在信息不对称情形。

1.2 制造联盟各方的利益函数

用R1、R2、R分别代表平台方、制造商和供应链制造联盟的利益，则在上述条件下，各方的利益函数可描述为：

(4)

(5)

(6)

2 制造联盟合作策略及利益分析

当n个主体从事某项经济活动时，相互合作会比各自单独行动创造的收益更多，Shapley值法是用于解决多人合作时分配合作收益的一种分配方法。设集合N={1,2,…,n}为n个参与人组成的联盟，合作收益R在n个联盟成员之间进行分配。φ(v)=(φ1(v),φ2(v),…,φn(v))为合作联盟的Shapley值，其中φi(v)表示在联盟中第i个成员所分得的利益，其计算式如式(7)所示；v为合作联盟的利益；T为包含参与人i的集合，即i∈T，T⊆N；t=|T|，即t为集合T中元素的个数。

(7)

因此，笔者针对供应链制造联盟协同合作的利益分配问题，通过探讨平台方与制造商非合作和合作时的收益，运用Shapley值法进行求解，并根据实际情况予以改进。

2.1 非合作策略下的利益分析

在非合作策略下，平台方与制造商之间是单周期Stakelberg博弈，博弈过程分为两个阶段。平台方作为领导者，首先以自身利益最大化为目标，确定自身的努力程度和奖金分配系数，制造商作为跟随者，在平台方做出决策后确定自身的努力程度。采用逆向归纳法，先从第二阶段开始计算，对R2求关于e2的一阶偏导，并令一阶偏导数为零，可得：

(8)

将e2代入式(4)得到：

(9)

对R1分别求关于e1、β的一阶偏导，并令一阶偏导数等于零，联立方程组，可以得到非合作策略下平台方从自身利益最大化出发所得到的最优奖金分配系数βD*为：

(10)

(11)

(12)

此时平台方利益的表达式为：

(13)

制造商利益的表达式为：

C-S

(14)

制造联盟整体利益的表达式为：

(15)

2.2 合作策略下的利益分析

因此双方只有改善协作水平，采取合作策略，才能提升制造联盟的效益。当双方在信息共享的情况下统一做出最优决策时，即从整条制造联盟利益最大化的角度出发，在制造联盟总收益函数R中，分别对e1，e2求一阶偏导，并令一阶偏导数等于零，可以得到合作策略下平台方和制造商的最优努力程度分别为：

(16)

(17)

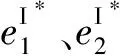
(18)

利用Shapley值法可将该合作利益分配给平台方与制造商，根据上述Shapley值法的计算公式可以得到：

v({1}-{1}))+

v({1、2}-{1}))

(19)

v({2}-{2}))+

v({1、2}-{2}))

(20)

φ1(v)=p1-p2+S+

(21)

φ2(v)=p2+C-S+

(22)

2.3 改进Shapley值法的利益分配策略

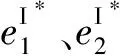
由此可计算出风险因素及努力效率因素的修正因子分别为：

最后，通过专家打分法可以得到风险因素及努力效率因素的权重占比f=(fx,fy)，fx+fy=1，于是可以得到参与人i的综合修正因子ΔZi=fxΔXi+fyΔYi，则参与人的收益调整量为Δφi(v)=RI*ΔZi。

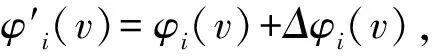
3 算例分析

假设客户与平台方签订了一份订单价值20万元的固定总价协议，且为了鼓励平台方匹配更高效的制造商，提供更高的制造服务质量，缩短制造时间，客户会在固定总价的基础上，给予平台方最高0.5%的奖金份额，具体比例依据平台方与制造商的协作效果而定。与客户签订合同之后，平台方向符合客户需求的制造商下订单，订单金额为18.0万元，并承诺将所得奖金的一部分分配给制造商。制造商接入云平台的接入成本为0.4万元，不接入云平台而自主寻求订单所付出的代价为1.5万元。平台方与制造商付出的努力对总产出的贡献权重分别为 0.6、0.4；双方的努力成本系数分别为0.4、0.6；双方的协同产出系数为200，奖金激励系数为0.5%，则平台方与制造商的利益分配模型可以表示为：

表1 双方非合作与合作博弈下的效益比较

(3)考虑风险因素和努力效率因素，改进原Shapley值法。通过专家打分法得到平台方和制造商遭受的风险损失C1、C2分别为1.5万元和2.0万元，风险因素及努力效率因素的权重占比fx、fy分别为0.5，0.5，即可以计算出双方风险因素和努力效率因素的修正因子以及两者的综合修正因子，从而得出在考虑这两个因素后利益在双方的重新调整量。相关的计算结果分别如表2和表3所示。

表2 基本参数计算结果

表3 修正因子及利益调整量

由表3可知，Δφ1(v)>0，说明平台方虽然承担了较小的风险，但因努力效率较高而增加了收益，以示激励；而Δφ2(v)<0，说明制造商虽然承担了较大的风险，但努力效率较低，因而收益有所减少。

表4 改进前后结果对比

综上所述，相较于非合作策略，采取合作策略是平台方与制造商的最优策略，原因在于当双方合作时，双方可以产生1+1>2的协同效益。对原Shapley值法的改进，并没有改变制造联盟的总体收益，而是改变了利益分配的方式。通过考虑双方所承担的风险的多少及为总产出所表现的努力效率的高低，给予相应的奖励或惩罚(收益的增减)，可以激励双方积极承担风险并提高努力效率。

4 结论

笔者构建了在客户的奖金激励策略下云制造平台运营方与制造商协同合作的利益分配模型。基于非合作策略和合作策略下的收益情况，考虑到决策主体承担风险的多少以及努力效率对于利益分配公平性的影响，对原Shapley值法进行了改进，使得分配更为公平。结果表明：①双方不合作时，云制造平台运营方可以以其主导地位，凭借先动优势先确定一个有利于自己的奖金利益分配比例；②非合作策略下双方的努力程度和收益以及供应链制造联盟总收益均不及合作时的结果。③改进后的Shapley值法有利于成员积极承担风险和提高努力效率。

总体而言，有效的激励策略和合理的利益分配方式是促使制造联盟成员加强合作的有效方法。同时，云制造平台运营方与制造商采取积极的合作策略，提升协作水平，改善努力效率，对于云制造模式下供应链制造联盟的稳定和发展具有重要意义。但是，笔者仅考虑单一制造商和云制造平台运营方相协作的情形，且假设双方均为风险中性，而实际情况中往往涉及与多个制造商合作的情形，因此涉及多个制造商、考虑决策者风险偏好的情形有待进一步探讨。