基于离散元法的深部裂隙岩体地层直井井壁稳定性分析

张士科，于锦彩，付德伟

(安阳师范学院 建筑工程学院，河南 安阳 455000)

0 引 言

在石油天然气工程中，井壁稳定问题通常是指井壁的变形、坍塌和周围地层的破裂，在钻井工程中这些都是十分普遍的难题。由于影响井壁失稳的因素比较多，例如：井筒的轨迹方向、原场应力的大小随深度的变化不断变化、岩石特征与裂缝分布、钻井液压力与地层渗漏等，所以井壁稳定性分析是一个十分复杂且耗时的工作[1]。但井壁稳定性分析能够有效地帮助提高钻井效率和降低钻井成本，为此，学者和工程技术人员开展了大量关于油气井在不同影响因素条件下井壁稳定问题的研究[2-3]。

在井壁稳定问题的研究中，通常由于无法直接实现地层特别是深部地层的实验研究，数值模拟研究就成了主要的研究方法，例如有限单元法[4-5]。但是采用离散单元法[6]并考虑天然裂缝和钻井液渗漏机理的油气井井壁稳定性研究相对较少。因此，以深部裂隙地层的油气井为背景，基于多场耦合分析理论，本文运用通用二维离散单元法程序(UDEC)[7]开展了不同钻井液压力值和井周围渗流引起的内摩擦变化的井壁稳定问题的研究，为优化钻井施工提供依据。

1 多场耦合理论模型

钻井过程是一个岩体结构场、应力场、温度场、渗流场等多场耦合的过程。

1.1 控制方程[8]

基于增量关系的应力-应变方程：

(1)

式中：dσij是总主应力增量，dεij是固体矩阵应变增量，dεkk是总应变增量，G是剪切模量，δij是克罗内克符号，α是Biot系数，β是热膨胀系数，dp是孔隙压力增量，dT是温度增量，ν是泊松比。

采用张量形式的位移平衡方程：

(2)

式中：uj,ji是位移张量，p,i是压力张量，T,i是温度张量。

1.2 渗流模型

钻井液向井壁周围地层渗流过程主要由流体在裂缝中的流速来决定，在裂缝中的粘性层流平均速度表达式如下[9]：

(3)

式中：a是裂缝的宽度，μ是流体的动粘滞率，g是重力加速度，dp是流体的压力差，l是在压力差之间的裂缝长度。

1.3 热传输模型

基于热弹性理论，井壁周围温度变化将引起岩体附加应力的变化，温度扩散方程表达式如下：

(4)

T(r,t)=T0+kij(Tw-T0)

(5)

式中：Cp是热容量系数，r是距离井筒中心的径向距离，T0是地层温度，Tw是井筒的钻井液温度，kij是热的传导张量。

1.4 渗流场与温度场耦合模型

基于多场耦合理论，裂隙介质的渗流与温度耦合方程：

(6)

式中：cf是流体扩散系数，cfT是温度扩散系数。

1.5 破坏准则

本文采用Mohr-Coulomb破坏准则来判断岩石破坏区域情况，进而分析井壁的稳定性问题，其函数的关系式如下：

τ=c+σtanφ

(7)

式中：τ是剪应力，σ是法向应力，φ是内摩擦角，c是黏聚力。

2 离散元法井壁稳定性模拟

本文运用UDEC软件裂缝生成器产生岩石结构场，并模拟分析井壁在温度场-应力场-渗流场(THM)之间的耦合作用的力学行为。

2.1 计算模型建立和边界条件

如图1所示，井壁稳定性分析的几何模型区域是一个垂直于竖直井的二维水平正方形，大小是4m×4m，模型的边界为固定边界。井眼位于几何中心，其直径大小为0.2m。为了方便研究钻井液(泥浆)渗漏对井壁稳定性的影响，设定泥浆渗漏范围在半径0.5m以内。图2为UDEC计算模型的天然裂缝分布模式和计算网格划分情况，任意天然裂缝由UDEC自带Voronoi裂缝生成器产生，在计算范围内有三条天然节理裂隙由节理裂隙生成器产生。为了提高计算精度，在泥浆渗漏区域进行了计算单元细化。

2.2 计算模型输入参数

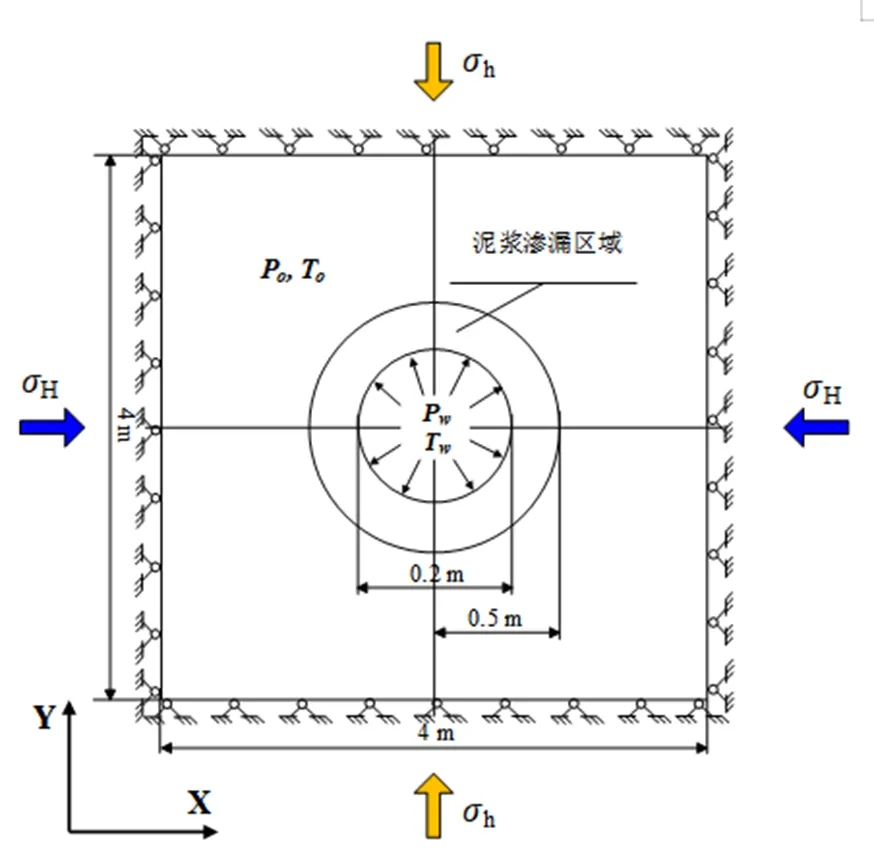
图1 几何模型和边界条件

图2 井壁周围的裂缝分布及计算模型

井壁稳定性问题分析区域位于2000m深的裂隙地层中，上层覆盖岩层产生的垂直应力为45.13MPa，计算模型区域所受的最大水平原场主应力大小为54.86MPa，最小水平原场主应力大小为36.34MPa，其方向如图1所示。初始孔隙压力P0=26MPa，弹性模量E=11GPa，泊松比v=0.29，剪胀角ψ=10°，岩石抗拉强度为1.17MPa，原场裂缝和岩石的内摩擦角为36°，泥浆渗漏区域的内摩擦角将从36°减小到25°。

原场地层的初始温度T0=100℃，热容量系数Cp=890J/kg ℃，热传导系数k=W/m ℃，井筒泥浆的温度Tw=120℃，泥浆的密度为1200kg/m3，泥浆的体积模量为0.1GPa，泥浆的黏结力为0.1Pa。

2.3 模拟结果与分析

为了模拟欠平衡钻井作用下井壁的稳定问题，钻井液液体压力值分别取12MPa，18MPa，24MPa进行模拟分析。位移作为井壁可视化直观物理变形和破坏的表现，被用来分析不同钻井液压力对井壁稳定性的影响。

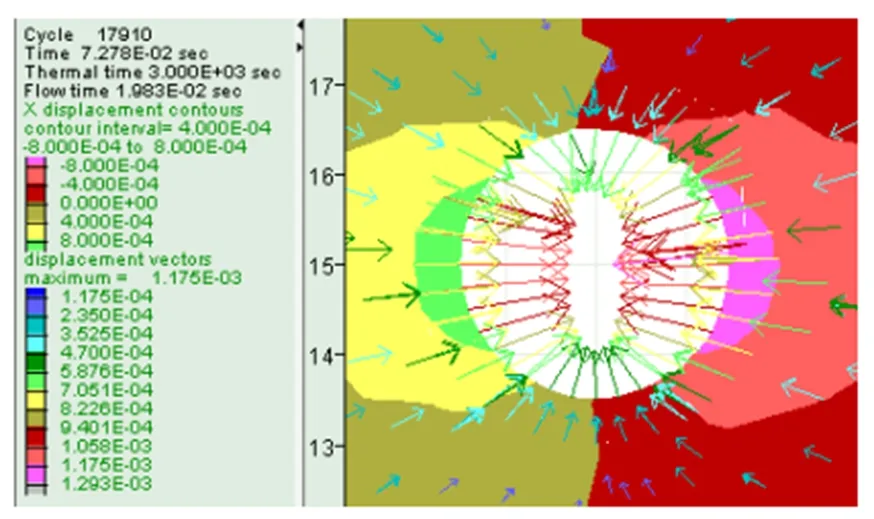
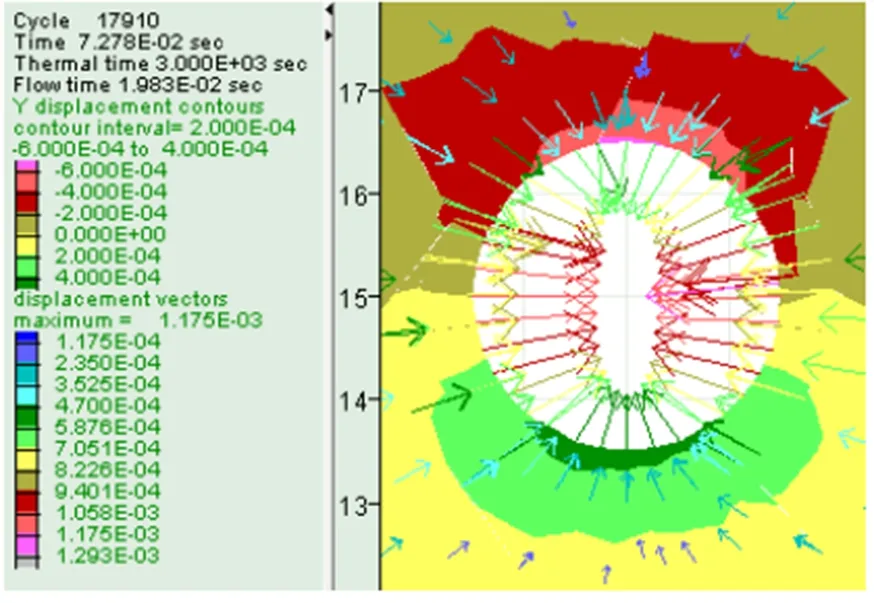
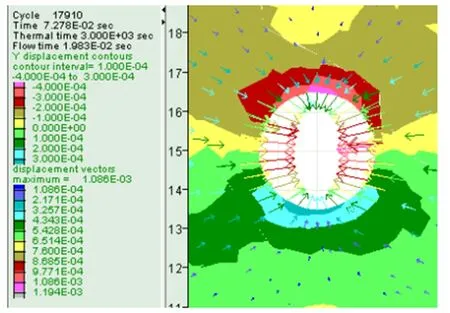
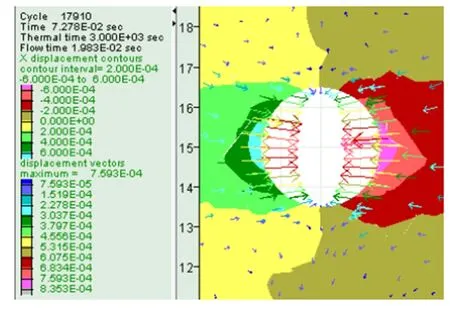
在钻井液液体压力值为12MPa时，X方向和Y方向井壁井径缩小位移分别如图3(a)和(b)所示，X方向的最大位移值是8×10-4m，Y方向的最大位移值是6×10-4m，最大位移向量为1.293×10-3。在钻井液液体压力值为18MPa时，X方向和Y方向井壁井径缩小位移分别如图3(c)和(d)所示，X方向的最大位移值是8×10-4m，Y方向的最大位移值是4×10-4m，最大位移向量为1.194×10-3。在钻井液液体压力值为24MPa时，X方向和Y方向井壁井径缩小位移分别如图3(e)和(f)所示，X方向的最大位移值是6×10-4m，Y方向的最大位移值是1.2×10-4m，最大位移向量为0.835×10-3。

从图3所示的结果可以看出，在不超过地层应力场最小压应力时，随着钻井液液体压力的增加，X方向和Y方向井壁井径缩小位移都将随之减小。当围岩的变形量或位移量达到一定数值时井壁就会因变形过大而失稳。井壁周围围岩的位移量作为井壁变形的显性表征，显然其围岩位移量不能过大，所以当钻井液液体压力与地层最小水平压应力大小相当时，最有利于井壁稳定，这一结果与参考文献[10]的研究结论相吻合。

(a)

(b)

(c)

(d)

(e)

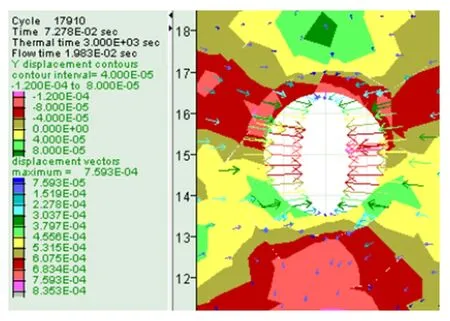
(f)图3 不同钻井液压力下井壁围岩位移图

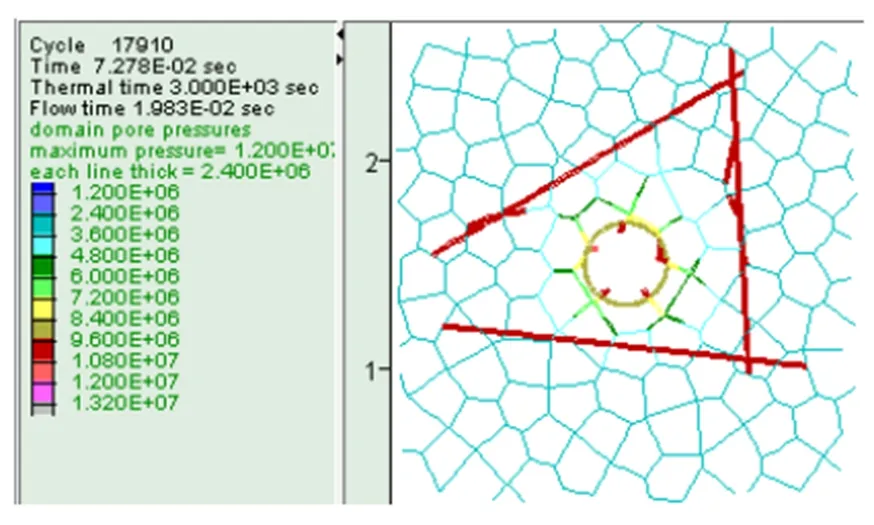
(a)

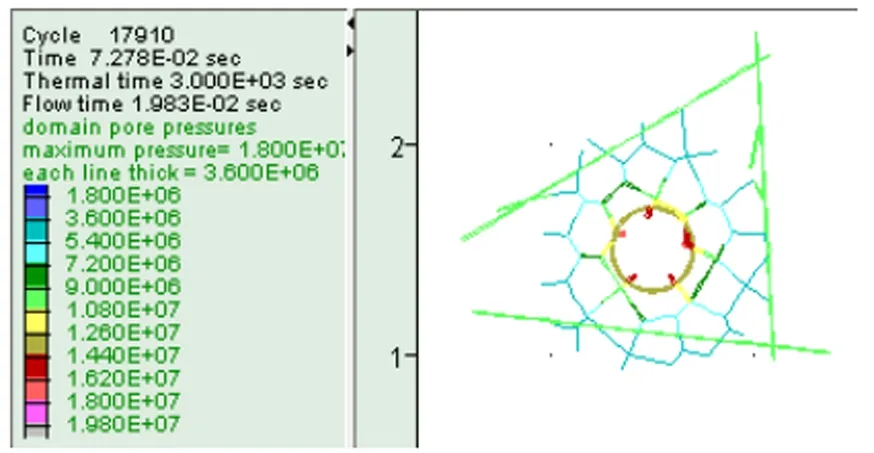
(b)图4 不同钻井液压力下泥浆渗流图

图4(a)和(b)分别是钻井液液体压力值为12MPa和18MPa 时，渗流场的压力变化情况。通过对图4(a)和(b)的比较可以看出，原有渗流场发生了明显的变化，钻井液在相同作用时间内，随着钻井液液体压力的增加，钻井液已经渗流到节理裂隙处，这与在渗透性较大深部裂隙地层中实际钻井施工的情况相吻合，较大的钻井液液体压力也会造成更多的漏浆而引起井壁的失稳，因此在钻井过程中不能为了单纯的减小井壁径向位移而单一的增加钻井液液体压力。

3 结 语

(1)在钻井过程中，钻井液渗漏到井壁周围岩体中从而导致岩体内摩擦角减小，当钻井液液体压力大小不与岩体地层最小压应力相当时，容易导致井壁周围围岩变形失稳。但是，当钻井液液体压力接近岩体地层最小压应力时，井壁周围围岩变形相对比较小。

(2)对于深部裂隙岩体，欠平衡钻井更有利于减少钻井液对井底的压持作用，从而减少钻井液流入到井壁周围围岩中，进而保持了井底的压力，增加了岩屑的上返，提高了钻井速度。

(3)井壁周围围岩的变形随钻井液液体压力的增加而减小，当钻井液压力与地层最小水平压应力大小相当时，基本实现了井内流体与地层压力的平衡，从井壁周围围岩变形的角度来说，最有利于井壁稳定。