汽油机进气道参数化优化设计

郭迁,韦静思,许汉君,武珊,丁尚芬,吕伟

(广州汽车集团股份有限公司汽车工程研究院,511434,广州)

在内燃机中,进气道的优劣对发动机的性能有着较大影响,合理的气道设计方案能够较好地组织缸内空气流动、增大气缸进气量、加快燃烧速度,从而提高内燃机的动力性及燃油经济性,改善尾气排放[1-3],因此对进气道进行合理的优化设计具有重要意义。

在进气道性能研究方面,国内外学者已经做了许多相关研究。Benajes等利用三维流体软件计算了某四气门柴油机可变涡流进气道的流动特性,并采用稳流实验进行了验证[4];Desantes等利用激光多普勒测速技术对两进气道的稳态流场及缸内湍流结构进行了研究,选择出了性能最优的进气道[5];刘德新等采用实验的方法对进气道的滚流运行进行了研究,对比了不同方案产生滚流的能力[6];周松等采用三维流体模型,分析了某螺旋气道倾斜角、气道位置等对流动特性的影响并采用实验进行了验证[7]。可以看出,研究人员主要利用数值模拟和实验研究两种方法,对进气道的流动性能进行研究并取得了一定成果。然而,在进气道优化方面,研究者主要根据三维流体计算结果,对进气道或燃烧室结构进行调整,使得进气道具有更好的流通性能[8-10]。但是,目前进气道优化主要是根据经验进行,具有一定的主观性及重复性,导致效率较低、周期较长。

为此,本文提出了一种基于进气道局部变形及旋转的参数化优化方法。采用控制点对气道局部变形及旋转进行控制从而实现气道变形的参数化,并对该模型进行了实验验证。对各控制变量及优化目标进行实验设计及贡献度分析,识别出对滚流比及流量系数贡献度较大的控制变量。以提高流量系数及滚流比为目标,采用第二代非劣排序遗传算法(NSGA-II)对识别的控制变量进行多目标优化,根据寻优结果得到性能最优的进气道几何模型。本文方法避免了经验优化的盲目性及主观性,提高了优化效率。

1 仿真优化理论

1.1 流量系数及滚流比

汽油机进气道的主要评价指标有流量系数及滚流比,都为量纲一参数,其中流量系数表征进气道流通能力的大小,决定气缸的进气量,滚流比表征缸内滚流运动的强度,对缸内空气混合、燃烧起着重要作用[11]。

(1)流量系数。流量系数Cf的定义公式[12]为

(1)

式中:ma为气缸实际流量(kg/s),通过实验或仿真得到;mt为理论流量(kg/s),公式为

(2)

其中,n为进气门数,ρ为缸内气体密度(kg/m3),A为气门座圈几何流通面积(m2),vt为等效速度(m/s),d为气门座圈内径(m),ΔP为进出口压差(Pa)。

(2)滚流比。在仿真及实验测量中,滚流比Tr取0.5倍的缸径截面处数据进行计算分析,Tr的定义为

(3)

式中:ωF为滚流截面位置实际角速度,rad/s;ωM为发动机理论角速度,rad/s。ωF和ωM的公式为

(4)

(5)

(6)

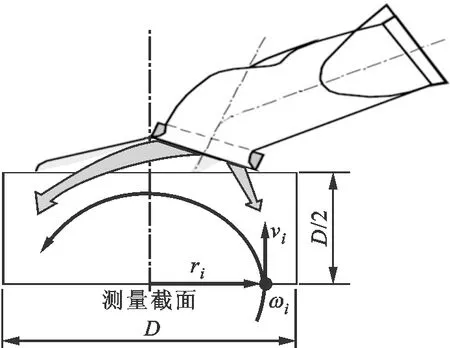
图1 滚流比测量示意图

1.2 贡献度分析

利用贡献度分析可以得到各设计变量对目标值的影响大小,其原理是在实验设计中,根据样本点建立二次回归模型[13],即

(7)

式中:Y为优化目标值;xi、xj为设计变量;β0、βi、βi,i、βij为回归模型系数,表明各参数对目标值的影响大小。

(8)

式中Txi为归一化后的设计变量,变化范围为[-1,1]。将式(8)代入式(7)中,得到归一化后的回归模型,即

(9)

式中λ0、λi、λi,i、λij为归一化后的回归模型系数。将系数λi进行转换得到各设计变量对目标参数的贡献百分比δxi,公式为

(10)

1.3 NSGA-II优化算法

进化算法是多目标优化算法的重要分支,其中NSGA-II因求解的解集具有较高准确性和较好分散性而被广泛应用,其主要流程[14-15]如下:

(1)随机选择初始种群P0,通过复制、交叉及变异产生新的种群Q0,将P0与Q0合并产生种群R0;

(2)对Rt进行非劣排序,选取非劣前段F1,F2,…,Fi,其余丢弃;

(3)对选取的Fi按拥挤度进行排序,选择其中最好的N个个体组成Pt+1,对Pt+1进行复制、交叉及变异,得到Qt+1;

(4)若Qt+1满足条件,则终止寻优,不满足则与Pt+1合并成Rt+1,之后转到步骤(2)。

2 优化模型建立及CFD仿真模型验证

2.1 优化模型的建立

根据以往经验,汽油机进气道喉口位置形状及倾斜角对其流量系数及滚流比有着较大影响[12,16],因此在某汽油机上,提取进气道结构,增加进口稳压腔,设置局部变形控制点及整体旋转控制点,如图2所示。控制点变形示意图如图3所示。

在图2中:一方面将喉口位置的上部区域及下部区域单独划分为变形区域,并布置相应的控制点及约束点,其中控制点控制相应的映射区域进行移动,达到局部变形的目的,约束点起着固定边界区域的作用;另一方面在气道周边建立控制点将气道整体包裹,控制气道整体围绕图3所示的旋转点在xy平面上进行旋转。

图2 进气道变形控制点示意图

图3 控制点变形示意图

在图3中:在局部变形区域,控制点1到控制点6对应的控制变量分别为S1到S6,控制变量初始值为0,控制点沿y轴正方向移动时为正,沿y轴负方向移动时为负;在整体旋转控制中,控制变量θ初始值为0,绕旋转点在xy平面逆时针旋转时为正,顺时针旋转时为负。根据实际气道布置确定各控制变量的初始值及变化范围,如表1所示。

表1 控制变量初始值及变化范围

提取该机型缸套、燃烧室、进气门、座圈及座圈加工面的几何模型,与进气道模型进行布尔运算得到进气道优化计算模型,为方便优化,进气门固定在最大升程10 mm处。

2.2 CFD仿真模型验证

各控制变量保持初始值时,得到气道初始设计模型,采用蜂窝状单元进行体网格划分,如图4所示,总体网格数约为53万,其中基础单元尺寸为3 mm,对喉口等关键区域及小尺寸结构的网格进行细化,边界层为3层,厚度为1 mm,采用1.5倍拉伸率。计算介质为空气,各物性参数为默认值。

图4 初始网格模型

采用STAR CCM+数值求解软件获取气道流动特性,具体模型采用稳态时间、可压缩流体、分离式求解器、k-ε湍流模型及全Y+壁面处理进行计算。进口总压设为6 kPa,出口静压设为0,参考压力为95.325 kPa,进出口温度均为25 ℃,壁面设定为绝热。进行进气道稳态流动计算,对结果进行处理,得到初始设计的流量系数为0.490,滚流比为2.88。

粒子图像测速(PIV)气道实验系统如图5所示,其原理是根据已知时间间隔内流场中微小区域的位移计算出速度矢量,其中激光源发出时间间隔为t的激光脉冲,照亮滚流比测量截面处,同时在待测区域散布合适的示踪粒子,施加固定压差,流量传感器测量系统流量,稳定后通过相机拍摄两次激光脉冲形成的待测区域图,通过数据处理最终得到每个点区域的速度矢量。

流量;Δp:进出口压差图5 PIV气道实验系统

针对上述机型制作相应的透明缸套及工装,进行PIV气道实验,得到滚流截面处轴向速度云图,如图6所示。实验时施加的压差与仿真一致(6 kPa),气门升程为10 mm,稳定后得到滚流截面处的轴向方向的速度云图(图6b)及相应的气道流量,处理后得到该气道的流量系数为0.475,滚流比为3.12。

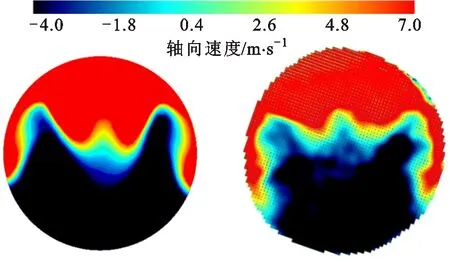
(a)仿真结果 (b)实验结果图6 滚流截面处轴向速度云图

从仿真与实验对比可以看出,流量系数误差为3.16%,滚流比误差为-7.69%。这是由于仿真模型中布尔运算后气道与导管安装面连接处无倒角,对模型进行了一定简化,而实际实验气道中该连接处存在不规则的倒角,导致仿真与实验存在一定误差,但均在10%以内。此外,通过对比图6a和图6b可以看出,滚流截面处的轴向速度分布一致、大小相近,表明该仿真模型具有较高的精度及可信度,可以用于后续的仿真优化。

3 流量系数及滚流比贡献度分析

根据表1中各控制变量的变化范围,采用最优拉丁超立方设计得到各控制变量的实验设计矩阵,共35组,如表2所示。最优拉丁超立方设计具有很好的空间填充性及均衡性,其原理是在n维空间中,将每一维变量范围等分为a个小段,在此基础上选取a个样本,使选取的样本均匀地分布在设计空间,同时保证每一个因子只被选取一次,即得到n维空间中样本点为a的实验设计矩阵。

表2 各控制变量实验设计矩阵

根据该实验设计矩阵,自动对气道进行变形,并采用宏命令的形式对变形后的气道进行布尔运算、流动计算及结果提取,得到各控制变量实验样本的流量系数Cf及滚流比Tr,如表3所示。

表3 实验样本计算结果

根据表2、表3,对各控制变量进行贡献度分析,得到各控制变量对流量系数及滚流比的贡献度,如图7所示,其中S1、S2、S3为下部变形区域控制点的控制变量,S4、S5、S6为上部变形区域控制点的控制变量。可以看出:对于流量系数及滚流比,S1、S2、S3的贡献度之和均高于S4、S5、S6的贡献度之和,表明下部变形区域对流量系数及滚流比的影响更大;靠近喉口位置控制点的控制变量(S1、S2、S4)对流量系数及滚流比的贡献度较大,而远离喉口位置控制点的控制变量(S3、S6)的贡献度则相对较小,进一步证明喉口位置对进气道性能具有较大的影响;气道轴向夹角对滚流比有着较大的影响,而对流量系数的影响则相对较小。

(a)流量系数贡献度分布

(b)滚流比贡献度分布图7 各控制变量贡献度分布图

为减少优化过程中的初始种群数,节约优化时间,通过贡献度分析选取对流量系数及滚流比贡献度之和大于10%的控制点的控制变量作为本文控制变量,即S1、S2、S4、S5及θ。

4 多目标优化结果

根据第3节分析选取S1、S2、S4、S5及θ作为优化变量,各变量变化范围保持如表1所示,其余控制变量保持初始值不变,对进气道进行多目标参数优化,优化目标为

(11)

在数值优化软件中采用NSGA-II进行优化,参数配置如下:初始种群数为12,代数为7,变异率为0.2,交叉率为0.8。寻优过程中根据各种群参数对气道进行变形、布尔运算、流动计算及结果提取,得到寻优过程中种群的流量系数及滚流比解集,如图8所示。可以看出:整体趋势显示流量系数越大,滚流比越小,两者成反比关系;解集上部的边沿解集为此次多目标优化的最优解集,与理论帕累托前沿最为接近;初始解位于解集下部边缘中间位置,表明NSGA-II优化方法具有很好的探索性能,能够使解集均匀分布在初始解周边,且使最优解集与帕累托前沿尽量接近。

图8 寻优过程中的流量系数和滚流比解集

本次优化的目标是在滚流比不恶化的情况下尽量提高气道的流量系数,因此保持初始解的纵坐标不变,作直线交于帕累托前沿,选取离交点最近的点作为本次优化的最优解,见图8,此点对应的流量系数为0.526、滚流比为2.87。相对于初始设计,本文方法在保持滚流比基本不变的情况下,使流量系数提升了7.35%,优化效果较好。

根据选取的最优解得到各控制变量的解,如表4所示。喉口位置根据S1～S4进行相应变形,然后再整体逆时针旋转5.816°。最终得到的进气道最优几何模型如图9所示。

表4 最优解下的各控制变量

图9 优化后的进气道几何模型

5 结 论

本文通过控制点对进气道局部变形及整体旋转进行参数化,建立进气道优化模型并对各控制点及旋转角度进行实验设计及贡献度分析,根据分析结果采用NSGA-II对进气道进行了多目标优化,结论如下:

(1)通过控制点对进气道局部变形及旋转进行参数化建模避免了全参数建模的复杂性,改动较小,对原机型有较好的适应性,同时实验证明该优化模型具有较高的可信度;

(2)实验设计及贡献度分析表明,本文方法能够很好地反映各控制变量对流量系数及滚流比的影响大小,进而选择贡献度大的控制变量进行优化,缩短优化时间;

(3)采用NSGA-II对进气道进行优化后,在滚流比基本不变的情况下,流量系数提升了7.35%(由0.490提升为0.526),优化效果较好。

综上所述,本文所提的进气道参数化优化方法步骤简单,效果较好,避免了经验优化的盲目性,提高了进气道优化效率。