考虑分布式电源与负荷不确定性的主动配电网重构
郑 源, 付晓刚, 轩艳文
(上海电机学院 电气学院, 上海 201306)
近年来,随着全球电力需求的增长,煤炭等化石燃料的消耗越来越多,带来了严重的污染问题。风力、光伏等分布式电源因清洁环保等特点受到青睐,但是由于各类分布式电源渗透率不断提高,配电网的运行管理日益复杂[1]。为了应对这样的情形,“主动配电网”应运而生。
主动配电网重构是解决大规模分布式电源(Distributed Generation, DG)接入配电网时造成的配电网络潮流分部不均、电压偏移等问题[2]的一种有效方法。文献[3-5]以最小化网络损耗为目标,在单个时间段面对主动配电网进行重构,但是没有全面考虑DG与负荷的时变性,仅考虑了DG或负荷的时变性对配电网进行动态重构。文献[6]基于信息熵划分时段以DG接纳能力为目标,用遗传算法进行配电网动态重构。文献[7]将一天分为多时段代理,将配电网静态重构。文献[8]考虑DG出力和负荷行为的不确定性,建立了相应的多目标规划模型。依据历史负荷曲线,挑选出特征场景,确定重构时的负荷情况,减少计算量。文献[9-11]通过Wasserstein距离指标划分光伏、风电、负荷的场景来处理他们的不确定性,但是并没有利用Wasserstein距离指标划分光伏、风电、负荷的场景后得到的场景概率。
因此,本文同时考虑DG与负荷的不确定性,基于Wasserstein距离指标与K-means方法提取主动配电网典型场景,提出了一种能适应多种场景的主动配电网多场景重构模型,利用典型场景的场景概率将该模型的多目标优化函数转化为单目标,进一步分析了主动配电网重构实际情况,提出改进的天牛群算法对兼顾DG与负荷确定性的期望有功网络损耗函数进行求解,采用网络重构编码策略减少不可行解的产生。最后采用修改后的IEEE33系统验证该方法的可行性和有效性。
1 DG和负荷不确定性建模
1.1 光伏发电数学模型
光伏发电受外界条件的影响较大,如光照强度、环境温度和空气湿度等。光伏发电的光照强度随机特性大多服从Beta分布[9],光伏发电的输出功率概率密度函数如下:
(1)
(2)
式中:Γ为伽马函数;α、β为Beta分布参数值;Pv、Pv,max分别为光伏功率和最大光伏功率;γ为光照强度;γa为额定的光照强度。
1.2 风力发电数学模型
根据文献[9]可知,Weibull分布是最常见的用来描述风速v不确定性的方法,其概率密度函数为
(3)
式中:c为Weibull的尺度参数;k为Weibull的形状参数。
风速与风电功率的关系为
(4)
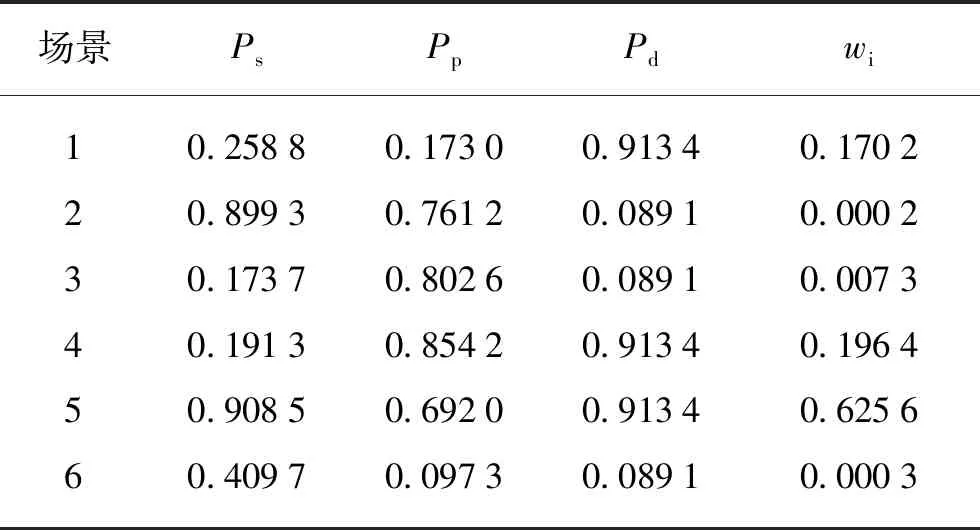
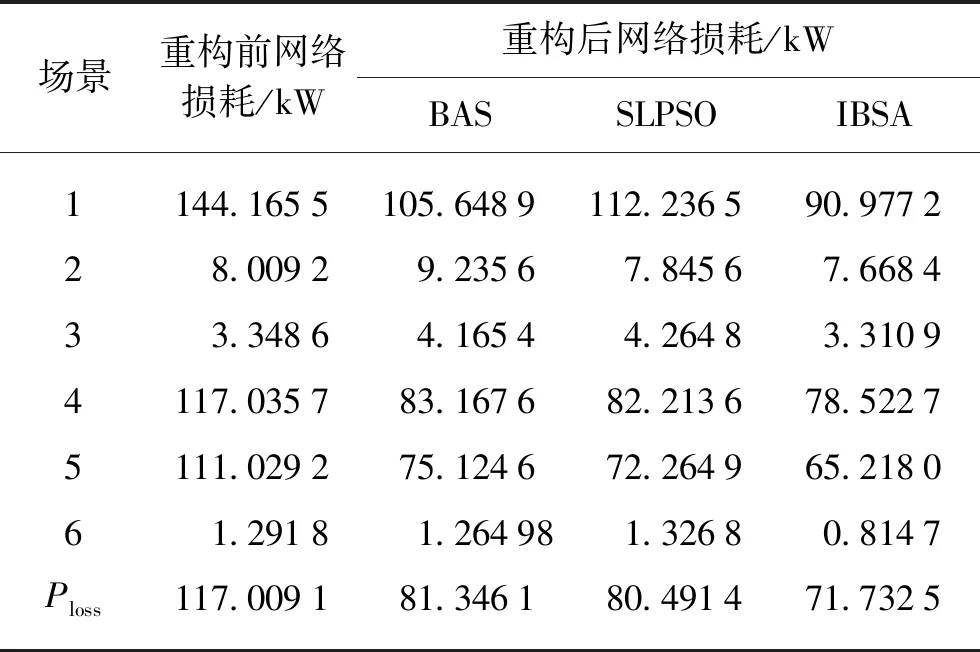
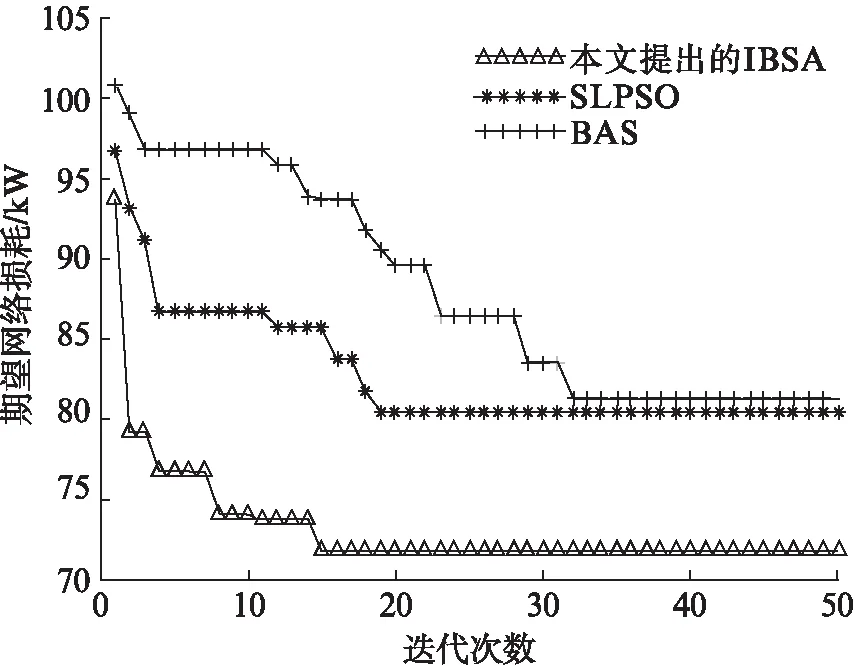
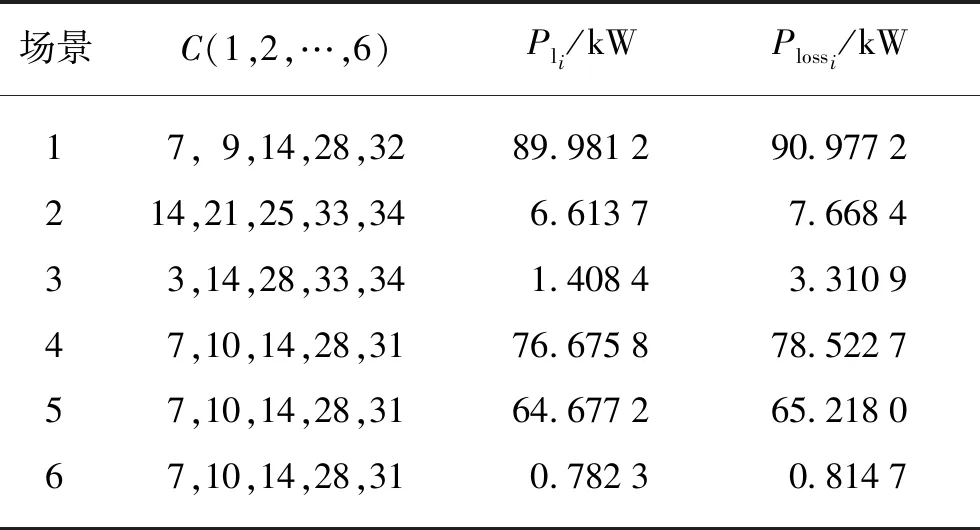
式中:vci为风电的切入速度;vr为风电的额定速度;vco为风电的切出速度;Pw为风电输出功率;Pw,max为风电的最大输出功率。0 (5) 式中:h=vr/vin-1;Pw=0时,f(Pw)=1-(f(vco)-f(vci));Pw=Pw,max时,f(Pw)=f(vco)-f(vr)。 由于负荷的出力受人的生活习惯影响较大,所以也存在不确定性,对特定区域的负荷模型可用正态分布进行描述,其概率密度[11]为 (6) 式中:Pi为有功功率;Qi为无功功率;μpi与σpi分别为负荷有功功率概率密度函数的均值和标准差;μqi与σqi分别为负荷无功功率概率密度函数的均值和标准差。 Wasserstein距离是对两个概率分布之间距离的度量,是求解各个离散分位点表示原连续概率密度函数的方法。对于任意的连续概率密度函数pc(x),使用Q个分位点的离散分布来近似表示连续概率密度函数,所以Wasserstein距离对任意连续概率密度函数的最优分位点zq(q=1,2,…,Q)可由式(7)求得 (7) 式中:r为阶数。 对于每个分位点的概率为 (8) 综上,风电、光伏和负荷在已知出力的连续分布函数的情况下,其基于Wasserstein概率距离的最优分位点zq可由式(7)求得,对应的概率Pq可由式(8)计算求得。文献[9]推导出了风力发电基于Wasserstein距离基的分位点方程,文献[10,11]分别推导出了光伏发电与变化负荷基于Wasserstein距离基的分位点方程,此处不再赘述。 多场景分析法能够将数学模型无法表述的不确定性转化为确定的场景来处理,避免了复杂的不确定性建模。通过Wasserstein距离对风力发电、光伏发电以及负荷需求进行场景划分,分别得到Nw,Np,Nl种对应的场景数,以及该场景的概率,则场景总数为Nw·Np·Nl种。场景数量越多反映不确定信息量就越大,但大规模的场景数量会增大计算负担。为了尽可能少的丢失信息量,同时降低计算量,本文采用K-means对场景进行削减。K-means聚类方法[12]算法结构简单、效率高,能够尽可能多地保持削减后场景的多样性而被广泛地使用。具体步骤如下: (1) 采用Wasserstein距离分别划分出风、光、负荷的Nw,Np,Nl种场景,以及每种场景对应的概率。 (2) 对得到的风、光、负荷的不同场景进行排列组合得到Nw·Np·Nl种场景。 (3) 确定需要聚类的场景数k,以及初始的k个典型场景的聚类中心(c1,c2,…,ck)。 (4) 根据适应度函数以类内距最小、类间距最大为目标,目标函数为 (9) 式中:EK为类内距,为第K类所有个体到该类中心距离的平方和;DK为类间距,为k个聚类中心距离的最大值。 (5) 对种群进行选择、交叉、变异产生下一代种群。 (6) 满足终止条件时,输出划分的各个典型场景的聚类中心以及概率。 为了得到适应k种典型场景的重构方案,所以本文将其作为一个多目标优化的问题处理。假设存在重构方案B可以使k种场景下的网络损耗(Ploss1,…,Plossk)同时达到最小,该方案即为最优重构方案,求解该方案的数学模型为 (10) 式中:Plossi为对应第k种典型场景下的网络损耗;Rj是支路j的电阻;fij是支路j的电流;kj为开关j的状态,0表示断开,1表示闭合。 k个典型场景的网络损耗函数即k个优化目标,一种重构方案在不同典型场景下产生不同的网络损耗。将每种典型场景的场景概率作为该场景下网络损耗函数的权重系数,可使该多目标优化问题转化为单目标优化问题。通过对式(10)进行线性加权,得到k种场景下的配电网期望网络损耗函数,对期望网络损耗函数进行优化时,得到重构方案能够使场景概率更大的场景网络损耗更小。目标函数为 (11) 式中:Ploss为期望网络损耗;wi为场景i的概率。 主动配电网重构约束条件如下: (1) 潮流约束等式 (12) 式中:Gij、Bij分别为节点i、j间的电导与电纳;Ui为节点i的电压;θ为功率角;PDGi、QDGi分别为节点i的分布式电源发出的有功功率和无功功率;PLi、QLi分别为负荷的有功功率和无功功率。 (2) 节点电压约束 Uimin≤Ui≤Uimax (13) 式中:Uimin、Uimax分别为节点i的电压最小和最大值。 (3) 支路容量约束 Si≤Simax (14) 式中:Simax为支路i的容量最大值。 (4) 分布式能源功率约束 Pimin≤Pi≤Pimax (15) 式中:Pimin、Pimax分别为节点i分布式能源功率的最小和最大值。 (5) 配电网网络拓扑约束。在配电网重构的过程中,应保证其拓扑结构为辐射状态,不存在环网结构和孤岛结构。 基本的天牛须算法[13](Beetle Antennae Search, BAS)原理是天牛在觅食过程中并不知道食物的精确位置,但可通过两个触须收集食物信息。天牛可判断左右须食物味道的强弱确定自身的飞行方向。如果右须收集到的味道强于左须,天牛下一步就往右飞,反之天牛往左飞,本质上属于差分算法的一类变种。其具有局部搜索能力强、参数少、收敛速度快的特点,但由于只有一个天牛,也存在全局搜索能力弱、容易早熟的缺陷。因此,本文将其与全局搜索能力较强的粒子群算法[14]结合提出一种改进的天牛群算法(Improved Beetle Swarm Algorithm, IBSA)。为了充分发挥两种算法的优势,自适应地调整天牛从自身触须获得的信息和从种群中获得的信息的权重,帮助种群在迭代前期搜索更加广阔的解空间,避免陷入局部最优,天牛的速度更新信息更多来自于群体,而随着迭代的进行天牛群向着全局最优进化,需要在全局最优解的附近进行更精细地搜索,所以,这时天牛的速度更新信息更多来自身的触须。 由于本文算例中的主动配电网一共有37个开关,解的维度较高。这样无法保证天牛群前期迭代的多样性,使其更全面地探索解集空间,鉴于此,将社会学习策略[15]融合到IBSA中,该方法在解决高维、复杂问题上受参数影响小,在迭代过程中每个天牛会向适应度值优于自身的天牛学习,适应度值最好的天牛会直接保留到下一代。速度和位置更新公式分别定义为 (16) (17) 式中:gmax为最大迭代次数;t为当前迭代次数;Yt为天牛从自身触须获得的速度信息;Vt为天牛从其他个体中获得的速度信息;vt和vt+1分别为t次和t+1次迭代时刻的速度;xt和xt+1分别为t次和t+1次迭代时刻的位置。 加入社会学习策略后的速度更新为 (18) 由于主动配电网中的开关只有闭合和断开状态,分别对应二进制中的1和0,故选择二进制编码方式对天牛群进行编码,求解式(11)的最优解,求得对应的开关组合方案。采用Sigmoid函数进行位置更新,算法的位置更新为 (19) 式中:rand为0~1的随机数。 主动配电网重构就是通过网络中分段开关与联络开关的重新组合,从而使网络损耗达到最小,在实际中配电网络设计存在公共回路开关操作,且配电网开关众多,开关数目众多,所以粒子维数巨大,会产生大量的不可行解,因此,需要对配电网络进行编码,从而提高算法的优化速率。 表1 IEEE33节点配电系统编码方式 图1 IEEE33配电网结构 网络环路开关矩阵定义为 SL=(aij)n×n (20) 开关粒子S所对应的SL矩阵为非对角矩阵,并且矩阵中有出现相同的行,所以会出现环路中公共开关被打开了3次,网络中出现了环网,故为不可行解。如果SL某一行全为0,说明该环网没有打开任何开关,就会产生孤岛,该粒子也为不可行解。综上,网络环路开关矩阵SL的秩R(SL) 以IEEE33节点配电网系统作为基础,在节点21与节点23分别安装额定功率为800 kW与400 kW的风力发电机DG1与DG2,其切入风速vci=5 m·s-1,切出风速vco=24 m·s-1,额定风速vn=11 m·s-1,该地区的风速在风机叶轮轮毂高度服从k=2与c=6.2的Weibull分布。额定容量为250 kW与200 kW的光伏阵列DG3与DG4,分别安装于节点11与节点17,其中光照强度服从α=0.41与β=1.38的Beta分布。天牛总数为20只,最大迭代次数为50次,社会影响因子为0.01。重构前的方案设置为不考虑风电、光伏、负荷不确定性的方案,即断开5个联络开关。 风电、光伏与负荷基于Wasserstein距离的场景划分结果如表2所示。zs、zp、zd分别为风力、光伏、负荷对应场景的概率;Ps、Pp分别为风力和光伏在该应场景下的实际功率占额定功率的百分比;Pd为该场景下负荷的需求情况。 表2 DG与负荷的场景划分 由表2可知,划分出的负荷场景是4个,风力发电与光伏发电场景都是6个,通过排列组合可以得到144种场景。利用K-means聚类方法将144个场景的聚类为6个典型场景,聚类结果见表3。 表3 主动配电网典型场景 所有典型场景重构前断开的开关组合为(33,34,35,36,37)。重构前与重构后各典型场景的网络损耗与期望网络损耗见表4。 表4 配电网重构后优化结果对比 由表4的优化结果可知,本文提出的IBSA算法得到的最优重构方案期望网络损耗相对于重构之前下降了38.69%,典型场景1、4、5占了整个配电网运行场景概率的99%以上,网络损耗对比于重构前分别下降了36.89%、32.91%、41.26%。对于社会学习粒子群算法(Social Learning Partide Swarm Optimization, SLPSO)和天牛群算法(Beetle Antennae Swarm, BAS)算法,期望网络损耗分别下降了31.21%和30.48%。通过求解该模型得到的最优重构方案能够降低主动配电网运行的网络损耗。 将本文提出的IBSA算法与SLPSO和BAS进行对比,每种算法在运行环境及基础参数相同的情况下,分别独立运行50次。3种算法分别记录50次实验结果的最小迭代次数、平均迭代次数以及寻优成功率,实验结果见表5。取各算法收敛效果最好的一次进行比较,收敛结果见图2。 表5 各算法性能对比 图2 各算法期望网络损耗收敛过程对比 结合表5和图2的3种算法性能对比可知,提出的IBSA在求解网络重构的开关组合方案时迭代次数更少、寻优成功率更高、期望网络损耗更小。结合了重构编码策略与改进方案的天牛群算法运用到主动配电网最优重构方案求解中具有更好的效果,得到的开关组合方案更加合理。通过IBSA得到最优开关组合方案为(7,11,14,28,32),该方案在重构时不存在环网结构和孤岛结构,进一步验证了提出的网络重构编码策略的有效性。 为了更进一步验证本文提出的主动配电网多场景重构模型的有效性,采用IBSA单独优化6种典型场景的网络损耗,与重构模型运用IBSA所求的解进行比较,验证该模型求出的典型场景网络损耗是否接近单独优化典型场景时的最小网络损耗,结果见表6,其中C(1,2,…,6)为单独优化每种典型场景的最优开关组合方案,Pli为该方案下单独优化典型场景的网络损耗,Plossi为主动配电网多场景重构模型所求方案下的典型场景网络损耗。 表6 单独优化结果与对比 由表6可知,通过对主动配电网多场景重构模型优化,得到的6个典型场景的网络损耗可知,该方案不仅能够降低主动配电网不同运行场景下的网络损耗,并且在该方案下场景概率大的网络损耗更接近单独优化典型场景得出的最小网络损耗。 通过分析主动配电网中分布式电源和负荷的不确定性对重构的影响,本文提出了多场景配电网重构模型、改进的天牛群算法以及网络重构编码策略,得出以下结论: (1) 在考虑风电、光伏和负荷不确定性的基础上,分别将基于Wasserstein距离的场景划分法和基于K-means的场景削减策略引入到主动配电网重构中,在兼顾负荷与分布式能源出力不确定性的情况下提取了6个典型场景。 (2) 为了得到一种能够适应6种典型场景的重构方案,将典型场景的网络损耗函数按场景概率进行线性加权,把多场景主动配电网重构模型转化为一个单目标的期望网络损耗函数。 (3) 考虑到主动配电网在实际重构时的特点,提出了网络重构编码策略,排除大量不可行解,并改进了BAS算法,提出了IBSA,对多场景主动配电网重构模型进行求解,提高了算法的优化性能。1.3 负荷需求数学模型
2 不确定性处理
2.1 基于Wasserstein距离的场景划分
2.2 风、电与负荷场景集削减
3 主动配电网多场景重构模型
3.1 优化目标
3.2 约束条件
4 多场景配电网重构模型求解
4.1 改进的天牛群算法
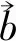
4.2 网络重构编码策略
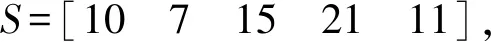
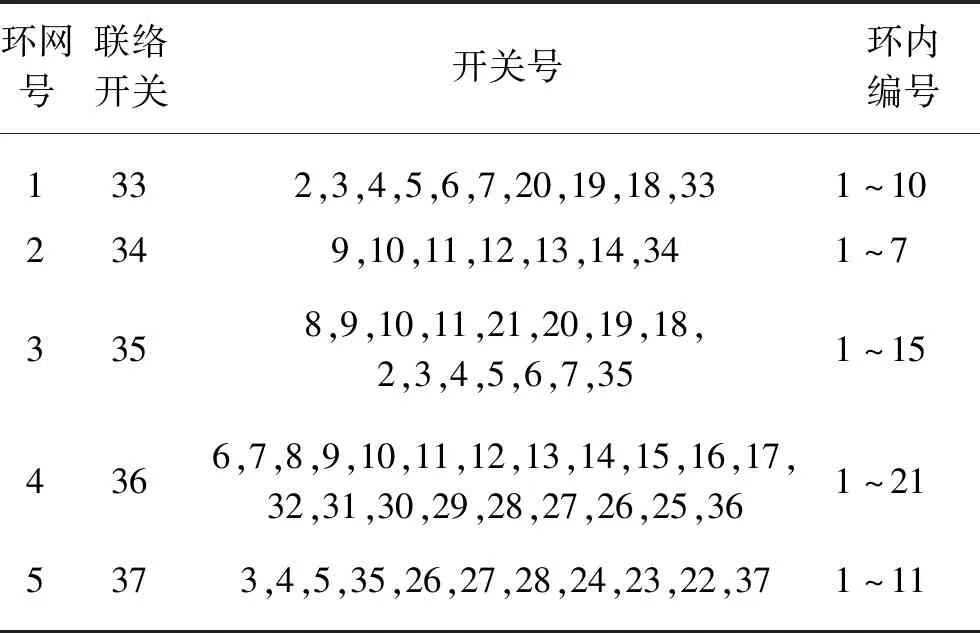
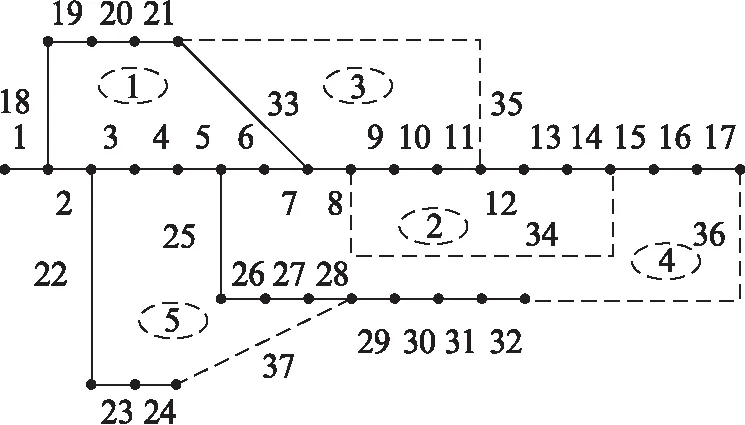

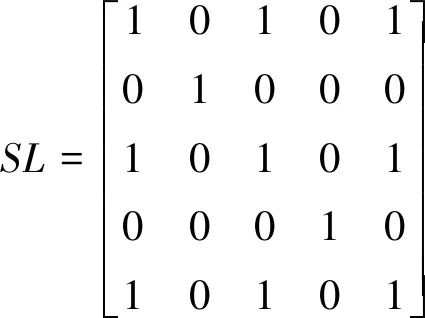
5 算例分析


6 结 论

