例谈数学思想方法的渗透——以“有理数”的章节教学为例

江苏省南通市崇川学校 薛海林

基于初中数学教育教学的视角，笔者认为，数学课程的内容一方面需符合社会的需求和学科的特质，另一方面还需与学生的认知规律相统一，它需囊括数学结论、结论的形成过程及数学思想方法.数学思想方法是对数学知识的本质认识，源自知识与方法，却又高于具体的知识与方法，也就是对数学知识的一种抽象概括.学生在动手实践、自主探究和合作学习的过程中，不断积累数学经验，领悟数学思想.因此，对于初中数学教育教学而言，数学思想的渗透应融合在教与学的过程中.

初中生已有知识结构不够完善，认知水平也较为薄弱，这就要求教师在数学教学中找寻适宜的切入点不断渗透和提炼，使之既能成为教与学的有效指导，又能有效促进初中生的有效发展.本文中，笔者以“有理数”这一章节的教学为媒介，以实践探究为手段，在数学思想方法方面做些尝试性阐述.

一、分类思想

所谓分类思想，就是基于事物本质属性的差异，把问题分为不同类别.换句话说，就是根据教学对象的共性与异性，将相同属性的归为一类，不同属性的归为另一类.分类思想是初中数学中运用较为广泛的一种重要数学思想，教材中不少问题的处理都是采用分类思想加以叙述的.本章节中引入了新知识“比0小的数——负数”，数的范围也扩展到了有理数.字母a可以表示任何一个有理数，探究数a则需恰当运用所学知识按照数的性质进行分类.

例1若a为有理数，-a一定为负数吗？

解：（1）当a＞0时，-a＜0；

（2）当a=0时，-a=0；

（3）当a＜0时，-a＞0.

分析：从解题过程可以看出，后两种情况中-a都不为负数.这一问题作为代数分类思想的“出发点”，教师要引导学生建构分类意识.

例2当|a|=3时，a的值为多少？

解：（1）当a＞0时，由|a|=3，得a=3；

（2）当a＜0时，由|a|=3，得a=-3.

例3若a、b是有理数，且ab≠0，请试着确定代数式的值有几种情况.

解：（1）当a＞0、b＞0时，代数式的值为3；

（2）当a＜0、b＜0时，代数式的值为-1；

（3）当a＞0、b＜0或a＜0、b＞0时，代数式的值为-1.

所以，代数式的值共有两个.

分析：绝对值的概念是初中概念中需要重点掌握的概念之一，其代数定义是分段出示的.在上述情况下，学生在解决与绝对值相关的问题时需要求绝对值，那么就需要从绝对值的定义出发，进行分类讨论.在进行分类时，需统一标准，克服思维的片面性，要满足不重复和无遗漏的原则，让分类中的每个对象仅属于其中的一类.

二、数形结合思想

恩格斯曾这样定义数学：数学是研究数量关系与空间形式的科学.因此，数形结合思想完美展现了数学的和谐统一.它是借助“形”的直观、整体、与几何性质相关等优势，以及“数”的精确和良好的运算数学及代数背景，有效地转化问题，实现解决问题的一种思想方法.其实质就是将问题中抽象的数量关系与直观的图形结构相融合，进而找寻解题思路的一种思想方法.

在学习完利用数轴表示有理数这一内容后，建构了“数”与“形”之间的桥梁，赋予了抽象数学关系直观意义.在教学“有理数”这一内容时，就可以进行数形结合思想方法的渗透.

例4有理数a和b在数轴上的大概位置如图1所示，请试着化简：|a-b|和|a+b|.

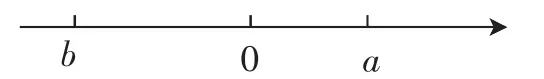
图1

分析：此例中充分运用数轴可以将绝对值的几何意义表达清楚.再如，在有理数加法法则和乘法法则的教学中，教师也可通过数轴形象、直观地帮助学生去理解和掌握概念的本质.

三、化归思想

所谓化归思想，即面对要解决的问题，通过某种手段或策略，将问题转化为基于思想的方法.化归思想本着化繁为简、化难为易、化高次为低次的“层层剥笋式”原则，使问题转化为自己能解决的问题.基本过程如图2所示：

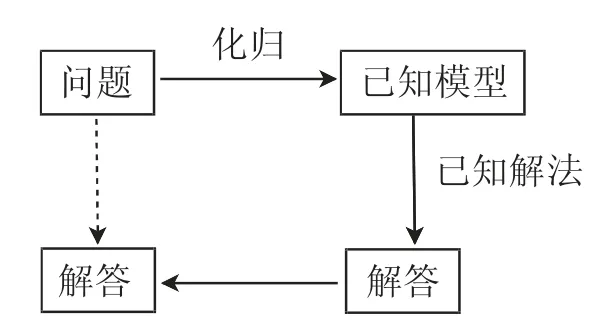
图2

①有理数的大小：在分类后，可以将相同符号的两个数转化成其绝对值（即正有理数）再比较两个数的大小；②有理数的加法、乘法、乘方：确定结果的符号后，根据小学阶段学生熟悉的非负有理数确定结果的绝对值；③有理数的减法：改变减数的符号后，将其转化成有理数的加法，使计算更为简单；④有理数的除法：首先将除数改为倒数，然后将其转化为有理数的乘法，简化运算.

综上所述，解决数学问题的过程其实就是将新知转化为旧知，实现问题解决的过程.

四、方程思想

在初中数学教学中，学生开始实现转型，由记忆型向理解型逐步转化，学生的理解水平也稳步提升，在这个阶段，教师需逐步训练学生的理解能力，而方程思想的渗透对学生学好数学起着关键性的作用.方程思想就是利用方程去解决一个问题.

例5若a-3和b+5互为相反数，请尝试求出代数式7-3a-3b的值.

在解决此问题时，从已知条件出发，可以找出与a和b相关的关系式，也就是方程：（a-3）+（b+5）=0.由此得出a+b=-2.

7-3a-3b=7-3（a+b）.将a+b=-2整体代入后，即可得出代数式的值.

“有理数”这一章中，涉及多个数学思想的渗透，在这里不再一一列举了.

作为一名初中教师，课堂教学就是引领学生思维活动的教学，也是渗透数学思想方法的过程.数学思想方法是数学的灵魂和精华.因此，在教学中，教师需要找到渗透数学思想方法的途径，使学生在学习数学知识的同时，能启发学生的思维，揭示数学的本质.只有经过反复训练和持续改进的过程，学生才能形成自己的数学思想方法运用意识，建构自己的数学思想方法系统.只有这样，才能充分发挥数学的内在动力，为学生的发展谋取长期利益，才能让学生学得轻松、学得扎实、学得有条理，持续适应将来的发展和需求.