启发潜能视域下的多边形内角和教学案例

李金和

大庆市新潮学校，黑龙江 大庆 163318

初中数学；启发潜能教育；课程融合

一、启发潜能教育概述

启发潜能教育是由美国教育大师威廉柏奇创立，这套教育理论的要旨是深信所有的人都是有能力、有价值、有责任的，而教育是一种通过彼此合作产生的协调活动，启发学生的潜在能力，让他们在愉快的环境下有效地学习。

启发潜能教育可以为营造、维持和提升真正温馨友善的学习提供指导原则。教师通过人、地、政策、活动和流程五个基本范畴（简称5P），就可以稳定、持续地施加压力，克服最艰巨的挑战，达到启发学生潜能的最终目标（五个核心理念）：乐观、尊重、信任、关怀和刻意性等理念[1]。

二、课程概述

本节课整合了北师大版初中数学八年级（上册）第六章第4节《多边形内角和》与黑教版初中信息技术八年级（上册）第三单元第15课《构图的开发》的教材内容，以项目学习的方式，以“提出问题”“分析问题”“寻找问题解决方案”为流程，学生在几何画板上建模，完成对多边形内角和公式的规律的探究。

三、启发潜能教育的核心价值和操作模式在本课中的应用

（一）“人物”的分析

教学对象是初中二年级的学生，已有的数学基础：已学过平行四边形，并且已初步了解四边形可分成两个三角形来求内角和，很容易想到提到的“分”“拼”“量”方法以及把多边形内角求和问题转化成加三角形的个数来求内角和的理念；已具备的信息基础能力：经过3.1节内容的学习，学生具有一定的几何画板操作基础，对利用几何画板来解决一些具体的实际的数学问题十分感兴趣。

课堂围绕小组活动开展活动，对于三十名学生而言，分为六个小组，每组设立小组长一名，小专家一名，小秘书一名，记录员一名，实验员两名。组内职务采用轮换制，这样精确分工设计的依据是关注每个人的价值，信任每个人，每个人分配到了具体的可操作的任务，提升小组成员高参与度，提高小组活动的高效性，同时，也体现了启发潜能教育的四个基本理念中的尊重、信任、乐观、刻意性。

基于对人物的多层次多方面的分析，为后面设计的一个课堂活动的决策支持。例如，在了解他们的几何画板基础上，利用知识迁移设计可操作的任务。这样任务对学生来说是可实现的，他们建模的过程也是表达信心的过程[2]。

（二）“地方”的设定

上课地点选在云教室，具备现代电子教室的全部功能，另设有希沃平板、电子书包等设施，为学生网络交互学习提供了技术的便利条件。

（三）“政策”的引领

培养创新能力一直是新课标的重要理念，《中小学信息技术新课程标准》中明确指出：要让学生具有应用信息技术的能力；要注意培养学生的创新精神和实践能力。引导学生发现生活中的问题，思考并寻找解决方法，使其以积极探索的态度，综合运用所学信息技术知识和能力，创造性地解决问题。

启发潜能教育是人本主义心理学思想在实践中的具体体现，教学生学会如何学习，掌握知识手段，而不仅在知识的本身。通过学生自己动手操作，积极参加“探究公式”的过程，让学生亲历数学公式发现过程、发现数学之美，增强学生用信息技术解决实际问题的能力、小组合作的能力。

（四）“活动”的设计

秉承教启发潜能教育的设计理念，“刻意安排”了3个子项目分三步完成。

【活动一】子项目1：创造性的思维训练——讨论多边形内角求和探究方案；

【活动二】子项目2：技术工具的储备——如何利用几何画板来支持探究方案？

【活动三】子项目3：创意式主题实践活动——探究多边形内角和公式。

三个子项目逐步学习，学生的自主探究贯穿于课堂的始终。最后学生画思维导图总结提升，梳理本节课脉络。

（五）详细的“过程”

【活动一：探讨多边形内角求和方案】

提出问题：我们熟知的正方形、长方形的内角是360°，那么任意四边形，如何求其内角和？

提示学生利用已知的知识和方法进行学习迁移，以小组的形式讨论、交流尽可能多地思考问题并说出自己的理论依据。

自主探究：方法一：“分”法：利用辅助线把四边形分为两个三角形（图1）。

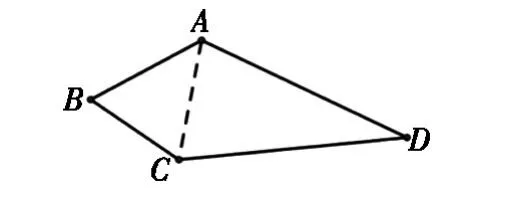
图1

学生探究出在四边形ABCD中，连接对角线AC，把四边形分解为两个三角形来求和，或者可以连接BD。接下来，我追问设AC与BD的交点O提出新的问题，在四边形中对角线的交点O是否可以变化？

四边形的四个内角都变成了什么角？又多出了哪些角？引导学生对O点位置进行分类[3]（图2）。

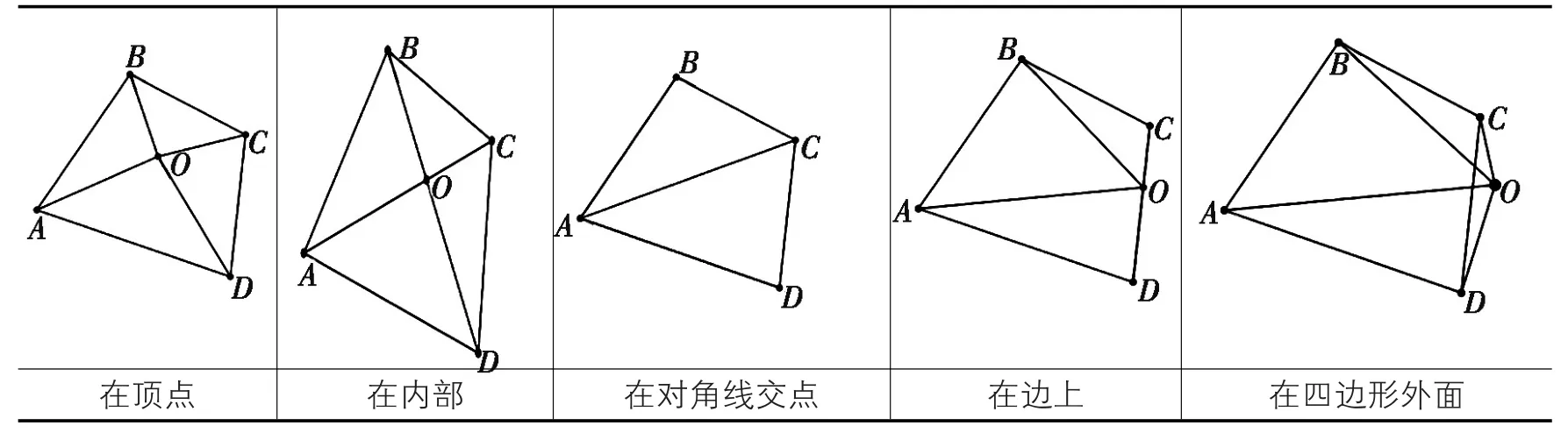
图2 O点位置变化图

方法二：“拼”法：把两个三角形纸板拼在一起，发现两个三角形内角和相加是360°（见图3）。

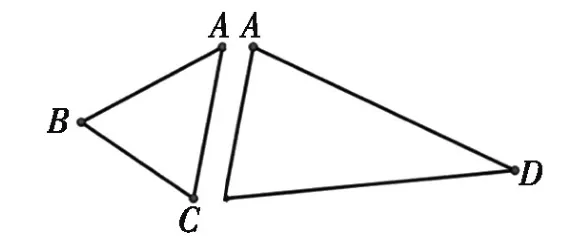
图3

学生探究此法是方法一的逆向思维，于是我顺势提出多边形（边数=n）可以由几个三角形拼成？学生又投入到热烈的探究活动中。

方法三：“量”法：任意画一个四边形，量出四个内角，相加求内角和（见图4）。

图4

学生探究借助量角器可以量角的度数，但是对于变数多的多边形不是一个好办法。

最后，三组学生探究发现，用连接对角线或者作平行线分割三角形的方法，可以解决任意凸四边形的内角和求解，为后续的多边形内角和求和奠定了方法基础。

当这三种主要方法被提出来后，我又引导学生能否借助几何画板构图来验证多边形的内角和。

学生通过自己动手操作、观察分析、合作探究、思考交流经历探索多边形内角和的过程，进一步提升了思维力，培养学生科学探究的精神。

【教学过程二：如何利用几何画板来支持探究方案？】

经过前面的学习，他们已经初步掌握了几何画板的简单构图、设计技术，但是要验证以上的方案还需要必要的技术指导，因此，我设计了多方案的技术支持，提供给学生可以参考的教材、微课、网站以及一些参考文献，更建议学生自己在网络上搜索答案，例如：如何做辅助线？如何度量内角？以此来支持他们设计的方案达成，学生们边学边做，我为他们遇到的问题答疑解惑。

笔者在课堂上反复强调“作品意识”，期望孩子们的学习成果是多样态的，是具有创新意识的，能充分体现每一位学生个性化学习方案。将学生作品提交到“作业空间”，利用云课堂的教师端的“击鼓传花”寻找一位“小老师”，授权给她/他批阅学生的作业权限，结合“加星”“点赞”“写评语”功能，评价“作业空间”同学的作业，实现真正的生生评价。

学生利用网络和微课获取、鉴别、使用信息的过程，也是主动适应“互联网+”等信息化生活方式，培养学生应用数字化工具解决问题能力的过程。

【教学过程三：探究多边形内角和公式】

利用“几何画板多边形内角和的推理.gsp”素材，拖动最上方横线上的P点（多边形的边数），会发现多边形的边数在不断地改变，图形也在相应地变化，图形中也相应显示出了对角线的情况。请学生观察图形的从一个顶点引出的对角线的条数、分割成的三角形个数从而来求出多边形的内角和，这样就把一个复杂的数学问题，转化成了简单的数三角形的个数问题，从而突破难点[4]。

最后点击右边“观察推理”按钮，对上述实践活动进行总结（见表1）：

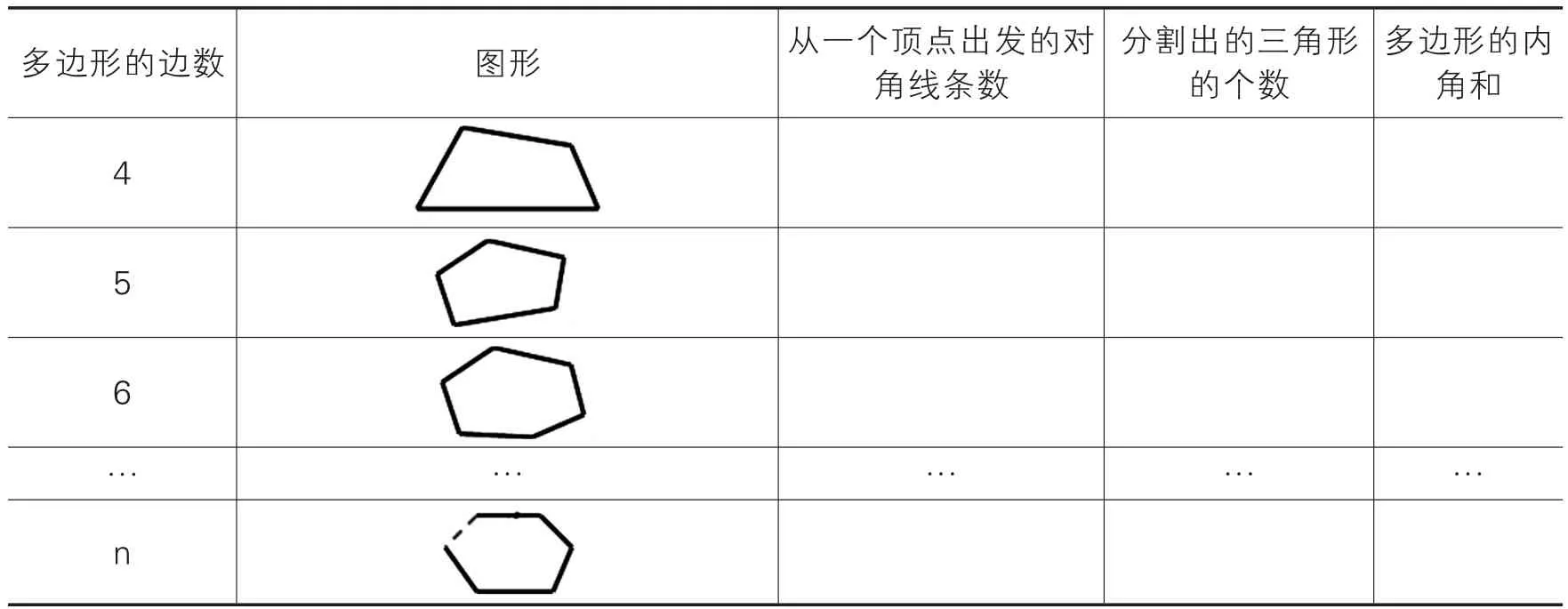
表1 多边形内角和规律

完成任务单中的任务：探究多边形内角和规律表格（表1），进而总结出多边形内角和的公式。

学生探究得出：从n边形的一个顶点出发，可以作出（n-3）条对角线，它们将n边形分成（n-2）个三角形，n边形的内角和等于180°*（n-2）。

最后的总结收获环节，利用思维导图软件Xmind，将今天的收获内容画出来[5]。

四、教学反思

本节课教师通过分析和刻意设计，启发潜能教育的人、地、政策、活动和流程五个基本范畴，稳定、持续地施加任务，让学生围绕“探究多边形内角和公式”这个项目开展探究活动，整节课学生沉浸在探索研究的乐趣中，通过有思维含量的数学活动，引导学生观察、体会、归纳、概括解决数学问题的一般思路，学生从中感受到了整合课程的乐趣，较好地达成了本节课的教学目标。