水下航行器的悬停与回旋特性研究*

刘 曜 ，沈建锋

(1 中国船舶重工集团公司第713研究所， 郑州 450015； 2 河南省水下智能装备重点实验室， 郑州 450015；3 中国人民解放军海军装备部， 北京 100000)

0 引言

水下航行器可应用于海洋探测、海底管路维修、海洋打捞等工作，有效地解决了人们深海作业的难题。海洋探测、打捞等作业活动，需要水下航行器具备稳定的悬停能力和回旋特性，因而文中针对水下航行器的悬停和回旋特性进行了仿真研究。

1 水下航行器六自由度操纵性方程

1.1 坐标系定义

航行器坐标系：坐标原点位于航行器浮心，ox轴与纵轴重合指向航行器头部，oy轴居于纵对称面，指向上方。地面系：坐标原点在航行器初始运动时浮心对应水面位置，ox0轴指向初始运动方向，oy0轴铅垂向上。速度系：坐标原点位于浮心，oxv轴始终与速度矢量方向重合，oyv轴在航行器纵对称面，指向上方。

以上3种坐标系均为右手直角坐标系，z轴由右手法则确定。

1.2 动力学方程

动力学方程组在航行器系中建立，航行器系的原点位于水下航行器浮心。设航行器运动的角速度ω及浮心处的速度ν在弹体系中的3个分量分别为ωx、ωy、ωz、νx、νy、νz；航行器的质量为m；质心在弹体系中的坐标为(xc、yc、zc)，根据动量和动量矩定理[1-2]：

(1)

式中:Fx、Fy、Fz、Mx、My、Mz分别为作用在航行器上的外力F和力矩M在航行器系中的3个分量，包括理想流体惯性力、流体粘性位置力、流体粘性阻尼力、浮力、重力、轴推螺旋桨推力、垂推旋桨推力、侧推旋桨推力和舵力(矩)。图1给出了水下航行器结构示意图。

图1 水下航行器结构示意图

1.3 运动学关系式

水下航行器转动是由3个姿态角(俯仰角θ、偏航角ψ、横滚角φ)描述，转动角速度(在航行器系分量为ωx、ωy、ωz)与3个姿态角变化率的关系式即为航行器转动的运动学关系式:

(2)

水下航行器浮心运动关系式、攻角和侧滑角关系式与方程(1)和(2)组成封闭可解方程。具体内容参见文献[3]。

2 水下航行器悬停

2.1 悬停状态仿真

针对水下航行器零浮力(浮力重力差为零)、零航速、零重心侧移量情况下的悬停状态进行仿真，仿真时间100 s[4]，悬停状态仿真结果见图2、图3。

2.2 重心侧移量对悬停状态的影响

针对水下航行器零浮力、零航速、0.1 cm重心侧移量情况下的悬停状态进行仿真，仿真时间100 s，重心侧移量对悬停状态的影响仿真结果见图4、图5。

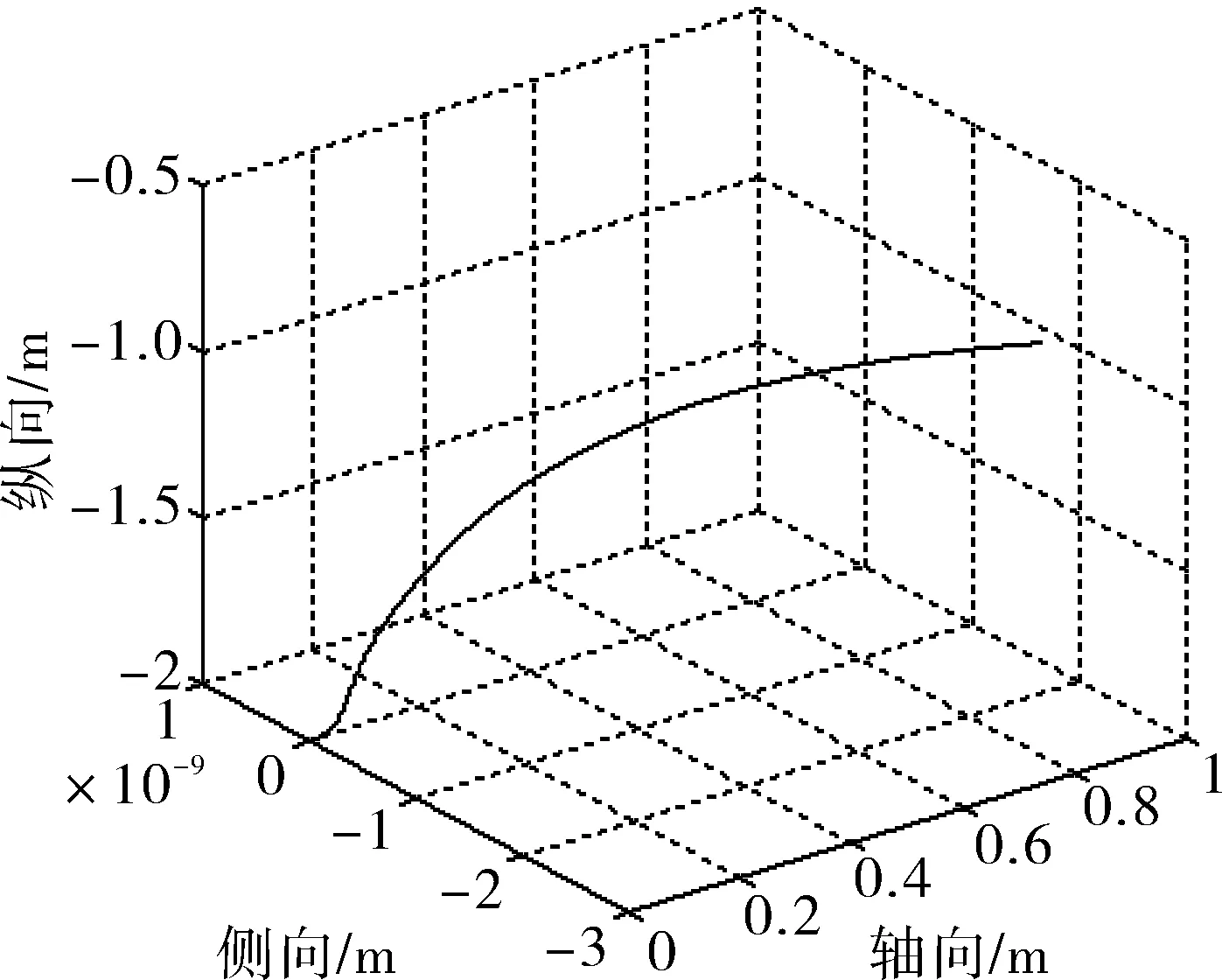
图2 悬停状态的空间运动曲线

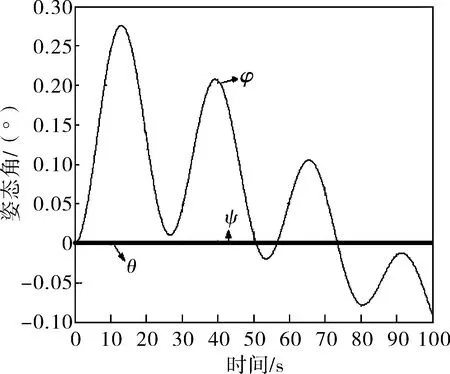
图3 悬停状态的姿态角曲线

2.3 悬停状态仿真结果分析

根据水下航行器悬停状态仿真结果可得：

a)在零浮力、零航速、零重心侧移量的状态下，航行器在水中具有保持固定水深和稳定的姿态的能力。在100 s的仿真时间内，航行器在轴向位移小于1 m，深度方向位移也小于1 m，侧向基本不存在位移；航行器的俯仰角θ、偏航角ψ基本在0°不变，横滚角φ在±0.3°间摆动。因而，只需要控制轴推螺旋桨、垂推螺旋桨间歇工作，就可实现水下航行器的定点悬停。

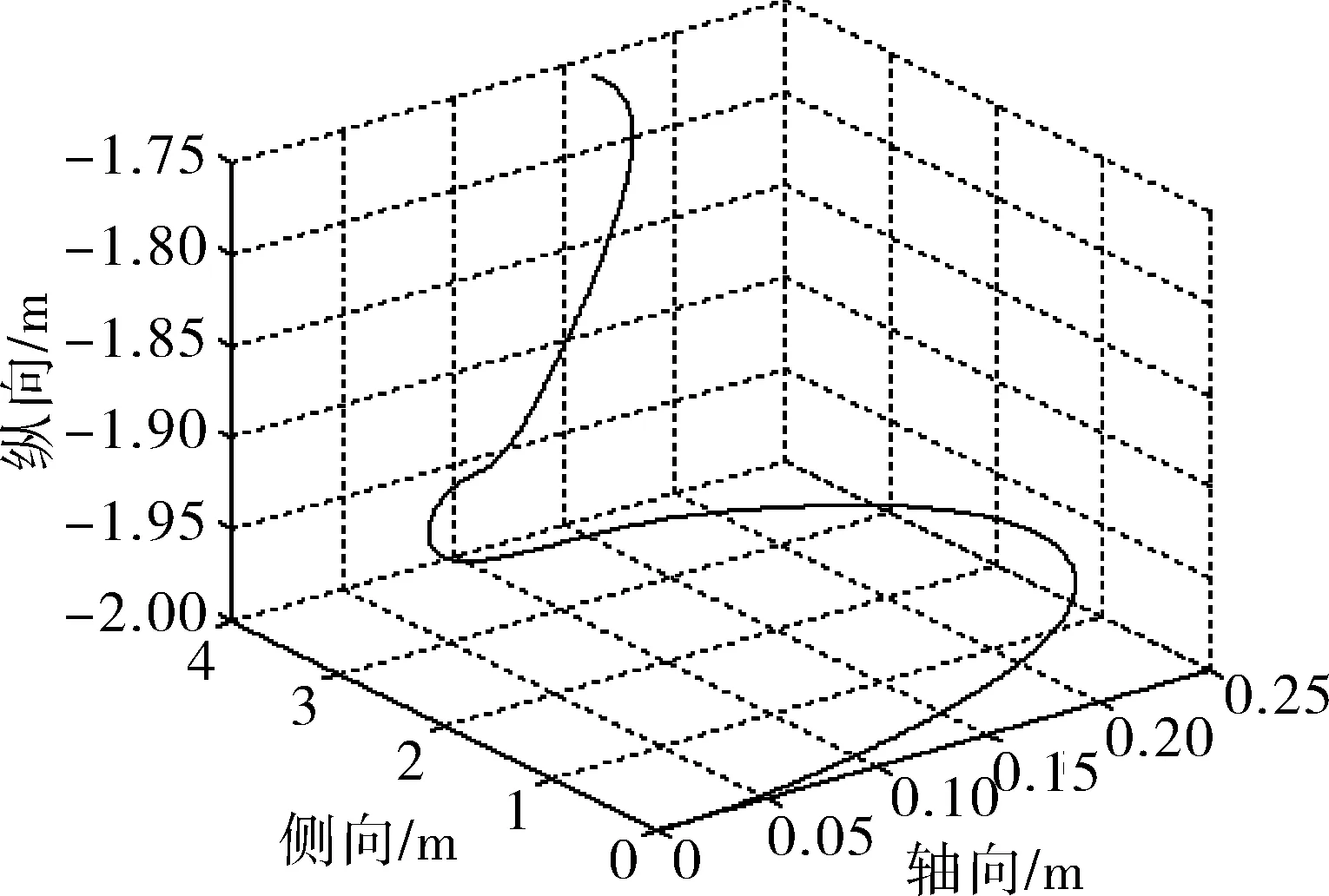
图4 悬停状态的空间运动曲线(0.1 cm重心侧移量 )

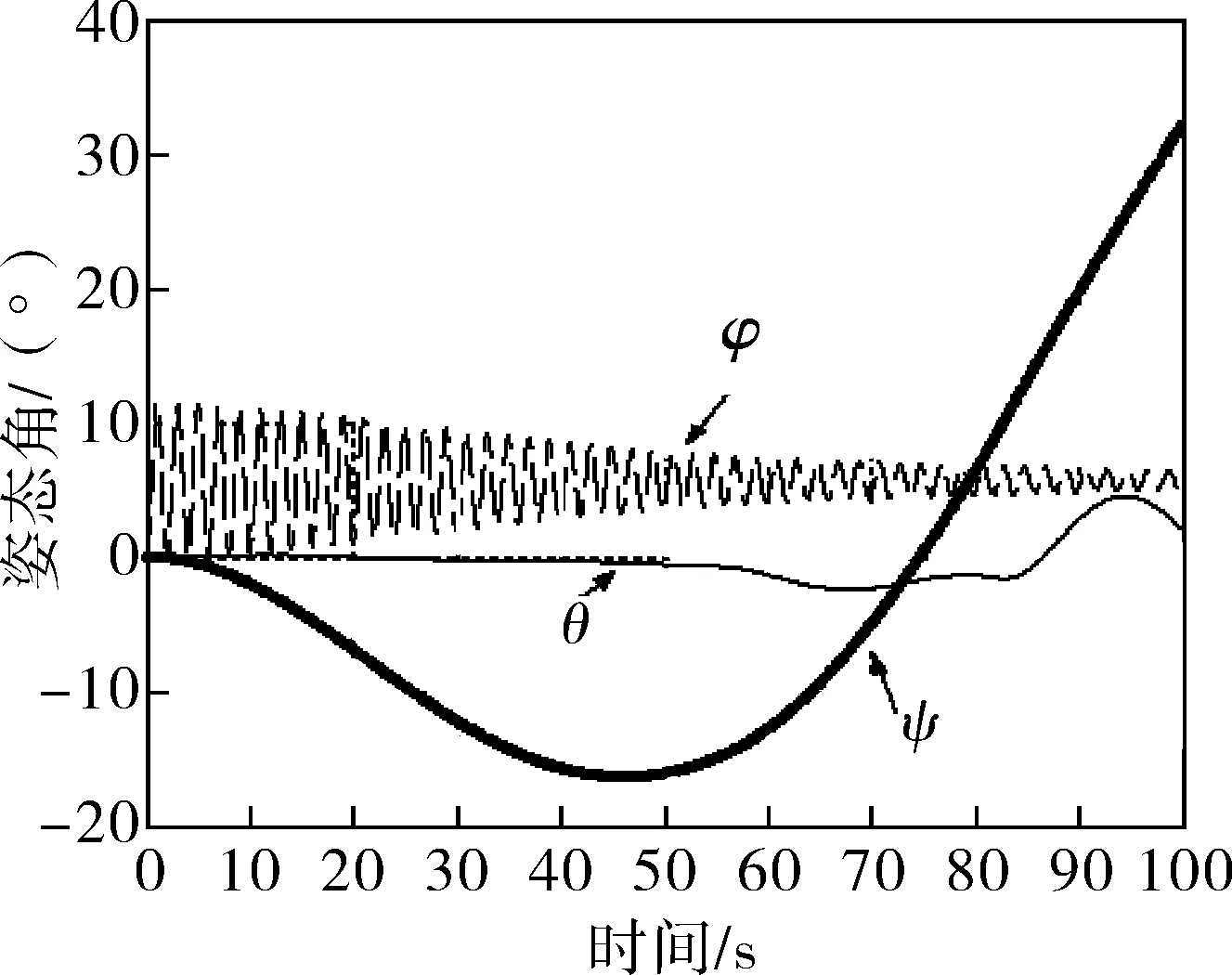
图5 悬停状态的姿态角曲线(0.1 cm重心侧移量)

b) 在零浮力、零航速、0.1 cm重心侧移量的状态下,航行器在水中同样具有保持固定水深的能力。在100 s的仿真时间内，在轴向位移、深度方向位移也小于0.25 m，但由于重心侧移量的影响，侧向位移增大到4 m；同样由于侧偏影响，航行器的俯仰角θ在-2°～6°间变化，偏航角ψ的变化范围增大到-18°～32°，横滚角在±12°间摆动且逐渐衰减。由此可见重心侧移量对航行器悬停的偏距和偏航角有一定的影响，但航行器状态是稳定、可控的。只要控制螺旋桨、舵联合间歇操控即可完成水下航行器的定点悬停。

3 水下航行器回旋特性

3.1 水平回旋状态仿真

水平回旋状态是水下航行器重要的一种运动模式，回旋半径、时间和回旋一周深度变化是航行器重要的特性参数[5-6]。针对5 N负浮力、航速3 kn、水平舵-1°、垂直舵25°的水平回旋状态进行了仿真。仿真时间200 s，水下航行器保持水平回旋状态，仿真结果见图6。

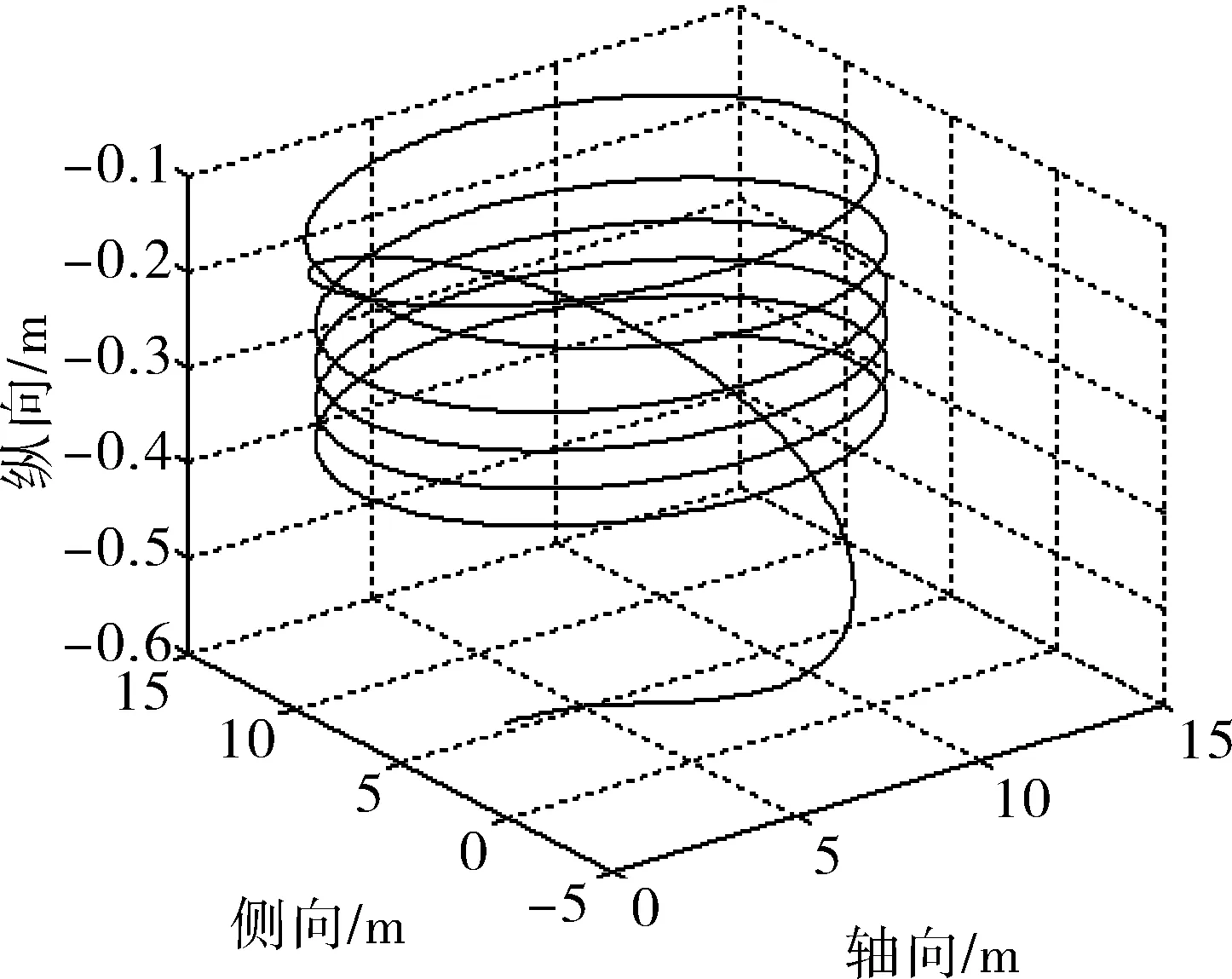
图6 水平回旋状态的空间运动曲线(5 N负浮力)

针对3 N正浮力、航速3 km、水平舵-1°、垂直舵25°的回旋状态进行了仿真。仿真时间200 s，水下航行器保持回旋下沉状态，仿真结果见图7。

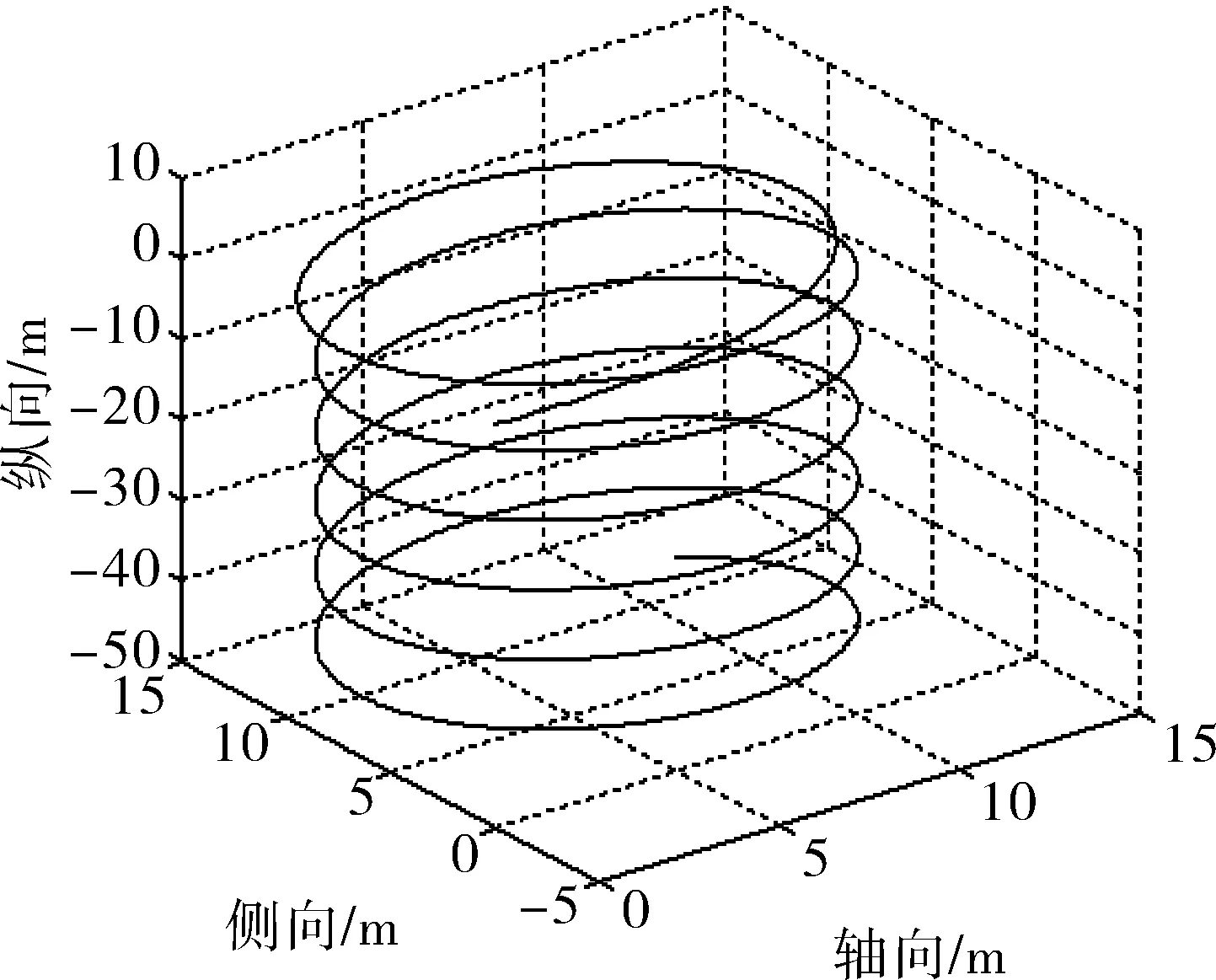
图7 回旋状态的空间运动曲线(3 N正浮力)

针对5 N负浮力、航速3 kn、水平舵-6°、垂直舵25°的回旋状态进行了仿真。仿真时间200 s，水下航行器保持回旋上浮状态，仿真结果见图8。

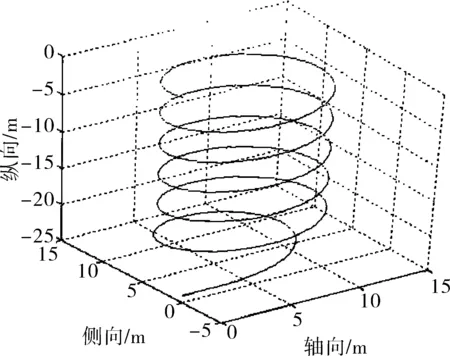
图8 回旋状态的空间运动曲线(水平舵-6°)

3.2 回旋状态仿真结果分析

根据以上仿真结果分析得：

a)航行器在200 s的时间内完成了6圈水平回旋，回转半径不大于7 m。回旋过程中航行器姿态稳定，俯仰角θ在±1°间变化、横滚角φ在-3°～3°间变化、偏航角持续线性增加。

b)浮力大小影响到航行器每回旋一周的深度变化。对于5 N的负浮力，每回旋一周航行器下降0.1 m的深度；对于3 N的正浮力，每回旋一周航行器下降8 m的深度，俯仰角保持-10°左右，横滚角在10°之内。可以通过垂推螺旋桨的控制来调节航行器每回旋一周的下降深度。

c)通过水平舵与垂直舵的联合操控可使水下航行器完成回旋上浮运动，当水平舵角为-6°时，水下航行器每回旋一周上浮4 m，俯仰角保持5°左右，横滚角在10°之内。

4 结束语

文中运用Matlab/Simulink模块对水下航行器的悬停与空间回旋状态进行了数值仿真，并对影响悬停和回旋特性的主要因素进行了分析，得到了水下航行器悬停和回旋运动的规律，可以直接在水下航行器的设计和操控中应用。