RBF神经网络在河流营养盐预测中的应用
黄伟建 张丽娜 黄远 程瑶


摘 要: 根据已监测到的水质数据进行预测一直是河流水质管理的重要组成部分,其中河流营养盐浓度是影响水质的根本因素。文中研究RBF神经网络在河流营养鹽浓度预测中的适用性,并与传统的时间序列预测模型:ARIMA进行比较。以朱衣河为研究对象,对河流营养盐主要成分之一的磷酸盐浓度进行预测。通过采集到的时间序列数据对两种预测模型进行仿真,并通过平均误差和均方误差的比较,证明基于RBF神经网络的时间序列预测模型具有较强的预测精度和良好的推广价值能力,在河流营养盐预测中有较高的实用性。
关键词: RBF神经网络; 营养盐浓度; 磷酸盐浓度预测; ARIMA; 仿真模型; 误差分析
中图分类号: TN711?34; TP39 文献标识码: A 文章编号: 1004?373X(2019)20?0156?04
Application of RBF neural network in river nutritive salt prediction
HUANG Weijian1, ZHANG Lina1, HUANG Yuan1, CHENG Yao2
(1. School of Information and Electrical Engineering, Hebei University of Engineering, Handan 056038, China;
2. School of Water Resources and Hydropower, Hebei University of Engineering, Handan 056038, China)
Abstract: River nutritive salt concentration is a fundamental factor affecting water quality. The applicability of RBF neural network in river nutrient concentration prediction is studied and compared with traditional time series prediction model: ARIMA. Taking Zhuyi River as the research object, the phosphate concentration is predicted, which is one of the main components of river nutritive salt. The simulation test of the two prediction models was carried out with the collected data of time series. By comparing average error with mean square error, it is proved that the time series prediction model based on RBF neural network has high prediction accuracy, high romotional value and better applicability in prediction of river nutritive salt.
Keywords: RBF neural network; nutritive salt concentration; phosphate concentration prediction; ARIMA; simulation model; error analysis
0 引 言
随着大数据分析技术的不断成熟,人们发现时间序列预测方法应用性极强,它不涉及数据产生的背景,任何可用时间序列表示的信息,均可用时间序列分析理论进行预测[1]。因此,有学者将时间序列预测方法中ARIMA预测模型(自回归积分滑动平均模型)应用到水质预测中,发现该模型既考虑了水质数据的随机波动的干扰性,又考虑了数据在时间序列上的依存性[2]。由于ARIMA预测模型通常适用于存在线性关系的数据,而河流营养盐浓度数据虽然有着时间上的依存性,但却是一种非线性时序数据。因此,ARIMA预测模型得到的预测结果并不理想。
为克服该缺陷,进一步提高预测精度,有学者发现将可以逼近任意非线性函数的人工神经网络技术与时间序列进行结合的预测模型,可以达到较高的预测精度[3];而且人工神经网络对任意函数具有自组织、自学习的能力,同时隐含层神经元采用了激活函数,使其具有非线性映射功能,可以逼近任意非线性函数[4]。其中,径向基函数(RBF)神经网络除具有极强的非线性映射能力,还有良好的泛化能力,网络结构简单,学习速度比一般网络快等优势[5],在其他领域也得到了广泛的应用[6?9]。故本文采用基于RBF神经网络的时间序列预测模型,对影响朱衣河水质的磷酸盐浓度数据进行预测,以期得到精确度较高的预测结果,为水质管理决策提供数据依据。
1 RBF神经网络
1.1 RBF网络
径向基函数(RBF)网络是一种向前网络,它以函数逼近理论为基础,能够逼近任意非线性的函数,同时具有很好的泛化能力和较快的学习速度。RBF神经网络由输入层、隐含层、输出层组成。输入层由输入节点组成,只传递输入信号到隐含层;隐含层由神经元的变换函数,如高斯函数、格林函数等辐射状作用函数构成,其中隐含层节点数由问题的实际需求来确定;输出层是对输入的响应,由输入节点组成。
RBF网络的主要思想是:将输入数据直接映射到隐含层空间,用径向基函数作为隐单元的“基”构成隐含层的空间,在此空间对输入数据进行变换,将在低维空间中的非线性數据变换为高维空间内线性可分。这种非线性的映射关系,通过径向基函数的中心点来确定。输出层则是通过隐含层的线性映射得到的,即网络的输出是隐含层神经单元输出的线性加权和。具体结构如图1所示。
图1 RBF神经网络结构

由上述RBF网络的原理可知,RBF网络主要涉及三种可调参数:RBF的中心向量[ci]、偏值[σi]、隐含层到输出层的权重[wik]。其中,RBF的中心[ci]的选取对网络性能至关重要,中心太近,会产生近似线性相关;中心太远,产生的网络会过大。根据这三种参数的确定,可以将RBF网络划分为很多种学习方法,最常见的是:随机选取中心法、自组织选取中心法、有监督选取中心法和正交最小二乘法(OLS)。本文采用基于OLS算法的RBF神经网络,OLS算法能够有效地自动选择中心,从而避免网络规模过大和随机选择中心带来的数值病态问题,同时有过程简单、学习速率高等优点[10]。
1.2 时间序列的RBF神经网络预测
基于RBF神经网络的时间序列预测模型,最主要的是需要确定好训练样本的输入和输出。为预测时间序列y(i)的值,以[X(i)=[y(i-n),y(i-n+1),…,y(i-1)]T]作为输入,n为历史数据长度,代表过去n天的历史数据。因此网络结构[11]可以表示为[y(i)=f(y(i-n),y(i-n+1),…,y(i-1))]。
由于时间序列有一定的复杂性,而且序列数据前后的关联程度大不相同。因此,采用不同的历史数据长度的预测模型,结果大相径庭。本文分别采用不同的历史数据长度,选取其中预测结果均方误差最小的历史数据长度,提高模型的预测性能。
2 实验过程
根据监测到的朱衣河连续325天的磷酸盐浓度数据,取前300天数据作为训练样本,后25天浓度作为预测验证数据。
2.1 ARIMA预测过程
1) 先对数据清洗,错误及空缺数据采用前5天均值填补。然后将数据归一化预处理,并对数据进行平稳性检验,得到原始序列的自相关和偏相关图,如图2所示。
根据图2可知,原始序列并不平稳,自我相关性极高,且呈下降趋势。因此,对原始序列进行一阶差分处理,使磷酸盐浓度序列基本平稳,得到的一阶自相关图和偏相关图,如图3所示。
2) 模型定阶。ARIMA模型一般需要确定三个参数(p,d,q),p为自回归项,d为差分阶数,q为移动平均项数。由步骤1)可知,d=1时,磷酸盐浓度时间序列变为平稳。p,q的取值则根据逐步试探法来确定,得到磷酸盐浓度最有预测模型参数为ARIMA(8,1,9)。

3) 模型检验。估计的参数全部通过显著性检验,同时判断残差序列为白噪声,因此认为模型可以较好地拟合数据。
4) 进行预测。将朱衣河前300天的磷酸盐浓度数据作为训练样本,预测300天之后25天的浓度数据。
2.2 RBF预测过程
1) 数据预处理。对原始数据进行归一化处理。
2) 输入输出设计。本文经过多次尝试采用不同的历史数据长度的预测模型,最终确定选取历史数据长度为14的预测模型,即由n,n+1,…,n+13天的数据作为输入,第n+14天的数据作为输出。
3) 选择传递函数。RBF神经网络的预测模型需要确定隐含层传递函数。由于高斯函数是最常用的传递函数,而且具有径向对称、形式简单、光滑性好等优点,故本文选取高斯函数为隐含层传递函数,隐含层到输出层选择线性函数。
4) 参数设计。本预测模型需要设计的参数主要包括:网络训练的目标误差DF,隐含层神经元的数目MN以及分布系数Spread的大小。RBF神经网络的目标误差决定隐含层神经元的数目,目标误差越小,所需神经元数目越多。分布系数Spread的大小关乎函数近似平滑度,Spread越大越平滑,但Spread太大需要大量的神经元来适应快速变化,从而导致预测误差过大。本模型先将Spread设置为1,以1为步长依次递增至50。经过多次试验,本模型设置DF=0.001,MN=125,Spread=44。
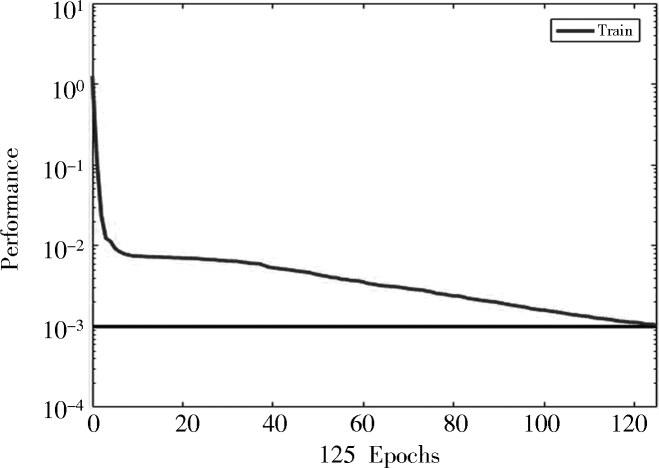
5) 训练样本。对样本进行训练,具体训练情况如图4所示。
图4 样本训练情况图

6) 进行预测。采用步骤5)得到的参数,预测301~325天的浓度数据。由于模型采用的是一步预测法,即每次预测一天的数据,在预测第i天的浓度时,以i-14,i-13,…,i-1作为输入;在预测第i+1天的浓度时,需将之前预测到的第i天浓度也作为输入的一部分。
2.3 实验结果
经过两种预测模型分别得到25天的磷酸盐浓度预测数据,将两种预测数据与实际数据进行对比可得到图5所示的对比图。
[8] 于岩,陈鸿昶,于洪涛.基于RBF神经网络的微博用户兴趣预测模型[J].计算机应用研究,2015,32(12):3555?3559.
YU Yan, CHEN Hongchang, YU Hongtao. User interest prediction model based on RBF neural network [J]. Journal of computer applications, 2015, 32(12): 3555?3559.
[9] 李瑞,张悟移.基于RBF神经网络的物流业能源需求预测[J].资源科学,2016,38(3):450?460.
LI Rui, ZHANG Wuyi. Prediction of energy demand in logistics industry based on RBF neural network [J]. Resources science, 2016, 38(3): 450?460.
[10] 单东,许新征.基于径向基神经网络和正则化极限学习机的多标签学习模型[J].模式识别与人工智能,2017,30(9):833?840.
SHAN Dong, XU Xinzheng. Multi?label learning model based on radial basis neural network and regularized limit learning machine[J]. Pattern recognition & artificial intelligence, 2017, 30(9): 833?840.
[11] 周志青,邹国防,王磊,等.基于ARIMA/RBF?NN的时间序列水质预测模型研究[J].科技通报,2017,33(9):236?240.
ZHOU Zhiqing, ZOU Guofang, WANG Lei, et al. Time series water quality prediction model based on ARIMA/RBF?NN [J]. Bulletin of science and technology, 2017, 33(9): 236?240.

