方格网法土(石)方计算的参数选择与误差分析
赵治华

摘要:本文分析了目前流行的方格网法计算土(石)方开挖回填计算时,如何选择计算参数与地形特征要素,并通过各种参数和地形特征要素之间的误差分析与对比,从而确定在不同地形特征要素情况下合理、正确的参数选择,以提高土(石)方计算的精度。
关键词:方格网法;计算参数;误差分析
在数字化测图非常普及的时代,作为场地平整土(石)方计算的首选方法——方格网法,以它简便直观,易于操作的特点,深受广大技术工作者的青睐,因此这一方法在实际工作中应用非常广泛。方格网间隔计算参数可以是5m、10m和20m,也可以是任意值,但在实际的计算中一般多采用10m×10m的方格网。而方格网间隔到底存在多大的误差,误差的主要来源在哪里,如何降低计算误差,目前没有明确的规范与要求来统一这个技术范畴的参数。由原理可知,方格的宽度越小,计算精度越高。但如果给定的格网间隔的值太小,超过了野外采集的点的密度也是没有实际意义;如果给定的格网间隔的值太大,就会出现计算误差的增加。如何合理、正确地计算出结果,就显得尤为重要。
一般工程在“三通一平”的阶段地形图的比例尺为1∶500和1∶1000两种,本文均以比例尺为1∶500地形图为例。在《1∶500_1∶1000_1∶2000外业数字测图技术规程》中规定,比例尺为1∶500地形图的地形点平均间距25m,在地形图整饰
阶段,为美观起见,地形点离散后的间隔也就在20m左右,就作为正式图纸成果发布提交了。
1.土(石)方计算参数的分析
1.1CASS9.1的方格网计算原理
该软件的方格网计算土(石)方量是根据实地测定的地面点坐标(X,Y,Z)和设计高程,通过生成方格网来计算每一个方格内的填挖方量,最后累计得到指定范围内填方和挖方的土(石)方量,并绘出填挖方分界线。程序系统首先将方格的四个角上的高程相加(如果角上没有高程点,通过周围高程点内插得出其高程),取平均值与设计高程相减。然后通过指定的方格边长得到每个方格的面积,再用长方体的体积计算公式得到填挖方量。
由此可见,地形点的高程值是计算土(石)方的关键参数,并由其疏密程度决定方格网的间隔值。
在山区地貌特征的数字化的地形图中,等高线就可以作为高程点加密的首选要素。在地形点稀疏的地形图中,一般地形点的平均间隔在25m左右,理论上只能计算方格网间隔值20m以上的土(石)方量,相对计算结果误差较小或比较合理、正确,而采用10m方格网间隔值来计算土(石)方量,显然是存在误差或不合理性的。
在CASS9.1软件中有一个等高线生成高程点的功能,如左图。利用这个功能,生成相对密集的高程点,就可以弥补高程点不足的缺陷。但前提是:等高线的属性一定要正确,因为等高线绘制的属性在非专业看来也就是一条曲线,但这一功能在还原地形点上是不能存在错误的。错误的属性,必然带来错误的结果,只有正确的结果,才能实现较小方格网值的土(石)方计算过程,并且把计算误差降低到最小。
在外业测量过程中,许多地形点没有删除的必要。不应该因为美观,而离散地形点,这样会丧失掉数字化地形图本身其他计算的精度要素。数字化图的判读和直接利用
(DTM数字模型的建立)是两个概念。以某工程的土(石)方计算为例就很直观看出计算误差的存在。
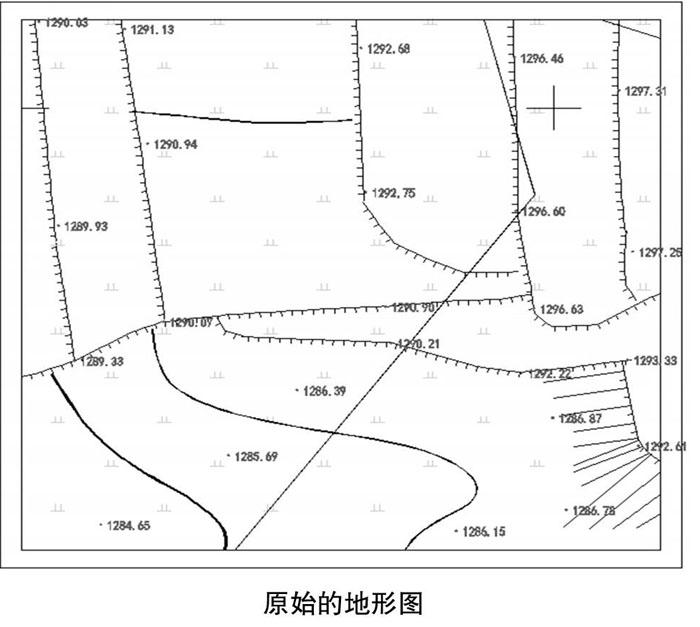
下图为原始的地形图,地形高程点的疏密程度在10m~20m之间,满足《1∶500_1∶1000_1∶2000外业数字测图技术规程》中规定。
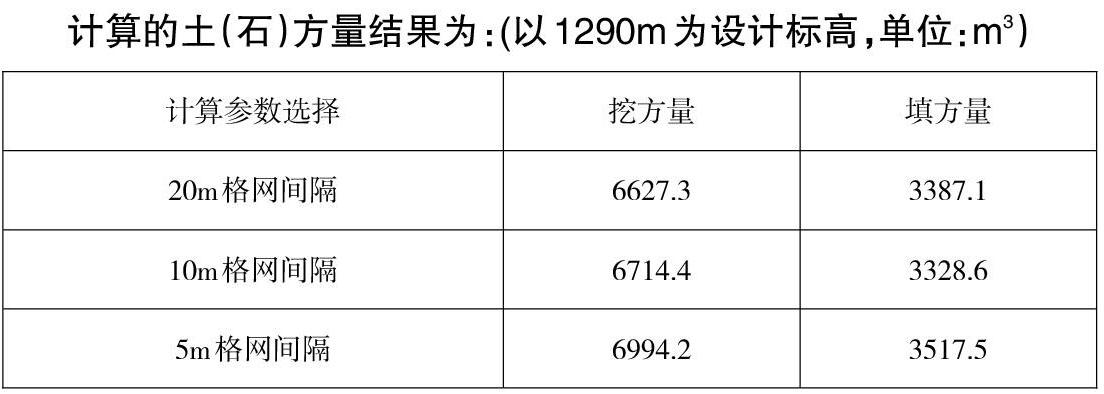
从上述计算结果来分析,格网间隔值越小,计算的填挖方量越大,这也是乙方施工单位追求的理想结果,而甲方业主单位则反之。这其中存在很大的系统误差,或者说人为因素。但如何准确地计算出实际量,就需要如实地进行地形特征要素的加密与取舍,真实地建立DTM数据结构模型,才能得到较为真实的结果。这也正是许多工程技术人员忽略的地方。
2.地形特征要素取舍的原则分析
在实际的测量数据还原原地形地貌特征点时,也就是形成DTM数字模型时,往往需要加密地形点,才能真实的反映出真实的地貌特征。下图为原始数据形成的DTM模型图。
从这张图上,我们明显地看出跟实际的地貌特征出入较大,而大家往往根据这个DTM数据模型在计算土(石)方量,即便是土(石)方计算的间隔再小,得出的土(石)方计算结论也存在较大的误差。要准确地建立DTM数据模型,就得进行地形点的加密工作。
加密地形点的位置一般在:A.陡坎的顶底位置;B.坡面的顶底位置;C.计算范围的边缘地带;D.其他地形变化的交界地带等。
加密地形点一般采用内插法进行。加密地形点不必顾忌地形图的整体美观性,要以DTM数字模型和实际地貌特征反复比对,直到符合客观实际为止。
下图为加密地形点后的地形图和加密地形点后的DTM数据模型。
从上述计算结果来分析,在地形点加密处理后,格网间隔值的大小,不再是决定计算填挖方量的决定因素,更在一定程度上体现出准确、公平、公正和合理。系统误差或者说人为因素在很大程度上得以解决。这才是作为一名工程技术人员需要把握的根本。
3.土石方计算的误差值的确定
如何确定土(石)方计算的误差,首要的因素是确定真值。就土(石)方计算而言,在地形点加密处理后,用三角网法计算的结果最接近真值。就本例而言三角网法的计算结果如下:
在确定了真值以后我们进行土(石)方计算的误差分析,土(石)方计算的误差分析表就是分析比照表。
从土(石)方计算的误差分析表可以看出,在土(石)方计算中,虽然没有较为明确的计算参数可选择,但从准确、合理、公正的立场出发,在土(石)方计算时,必須进行地形点的加密处理,在此基础上方可进行计算方法的选择。计算方法不是决定计算误差的主要因素,地形点的稀疏周密,才是根本上反映地貌特征的决定因素,也是决定计算准确性的唯一客观依据,这一点在山区不规则地形中,显得尤为重要。
在实际工程现场中,一般将土(石)方计算误差控制在5%~10%的范围内,认为是较为合理的,但也不能把计算误差看成土(石)方计算的参考值,随着土(石)方量的加大,计算误差理论上应该是越小的。就笔者经验而谈:1×104m3挖填量以内,控制在5%以内,1×104m3~10×104m3控制在3%范围内,10×104m3以上控制在1%~2%的范围内是较为合理的误差范围。
4.总论
综上所述,在我们的实际工作中,若较为准确计算出土(石)方挖填客观实际计算量,必须经过以下过程:
(1)客观准确地加密地形点,尤其是陡坎、坡面等。这往往是地形点较为缺失的地方,也是土(石)方计算的决定性特征。
(2)建立DTM数据模型。根据所反应的特征与实地对照,反复增加地形点,直到模型与实地一致。
(3)选择多种土(石)方计算方法,择其优者,得出结论。
(4)土(石)方计算的误差率,应该随着土(石)方计算量的增大而减小。
参考文献:
[1]《Cass91 For Aotocad 2008》广州南方数码科技有限公司编著,2012版.
[2]《工程测量规范》GB50026-2007,国家技术监督局和中华人民共和国建设部联合颁布.
[3]《1∶500_1∶1000_1∶2000外业数字测图技术规程》GB14912-2005中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会发布.
[4]万义有,李勇华,王小卫.土方量计算中的方格网法边长最优选择分析[J].科技资讯,2018(19):65-68.
[5]田旦,成国辉,徐景,熊仕稳.方格网法土方计算精度提高的改进方法[J].城市勘测,2017(03):148-150+170.
[6]邱文双.方格网法在复垦工程土方量计算中的应用[J].矿山测量,2017,45(03):114-116.
[7]杨永平,陈占,张晓伦.关于方格网法计算土方公式的探讨[J].昆明冶金高等专科学校学报,2016,32(05):57-61.
[8]曾怀恩,葛奎.利用方格网法计算复杂地形开挖土方量[J].地理空间信息,2016,14(09):82-84+8.
[9]张衡,李通,肖鹏,吴学超,徐花芝.利用方格网法计算土石方量的探讨[J].山西建筑,2016,42(04):217-218.
[10]刘宏宏.方格网法土石方计算与高程中误差关系的探讨[J].江西测绘,2016(01):57-58.
[11]廖小延,熊俊杰.方格网法计算土方量的应用分析[J].城市勘测,2015(01):155-158.
[12]粟晟,欧陆.南方CASS计算两期间土方与方格网法土方计算相结合准确计算土方量[J].中国井矿盐,2013,44(05):32-34+37.
[13]曹祥寅,赵崇阳.浅谈方格网法土石方算法在土石方工程中的应用[J].广东科技,2013,22(02):86-87.
[14]黄红镇.土方工程计算若干问题的思考——以FastTFT方格网法为例[J].中外企业家,2018(23):113.
[15]徐剑,王振.方格网法土方计算在公路服务区场地计算中的应用[J].工程与建设,2018,32(01):33-36.
[16]劉士霞.基于CASS方格网法土方量计算应用[J].水土保持应用技术,2018(01):34-35.

