员工脱岗与煤矿企业安全检查的演化博弈研究
宁 静,聂方超
(1.中国矿业大学(北京)能源与矿业学院,北京 100083;2.中煤科工金融租赁股份有限公司,北京 100031;3.中国矿业大学(北京)应急管理与安全工程学院,北京 100083)
矿工脱岗对于煤矿事故发生有直接影响,且一旦引发事故后果严重,因此降低矿工脱岗概率的研究十分有必要[1](本文所指“脱岗”还包括虽坚守岗位但并未尽到相应的职责)。安宇[2]通过统计分析某矿业公司违章记录,得出在该公司出现次数最多的不安全行为中,脱岗排在第6位。魏京天等[3]设计了一种脱岗检测系统,能够及时准确发现离开工作岗位的不安全行为,但是无法监测坚守工作岗位但并未尽到相应职责的脱岗。对于不安全行为,我国学者常用模糊聚类[4-5]、因子分析[6-7]、结构方程模型[8-9]等宏观方法展开研究,而对具体行为研究较少。
博弈论是研究具有竞争现象的数学理论和方法,近年来在不安全行为研究中有着广泛应用。如盖丽丽[10]通过构建矿工和检查人员的动态博弈模型,得出奖励约束机制具有一定的延续积累特性,为煤矿企业以奖代罚的管理方式提供理论基础。杨雪等[11]以进化博弈论为基础,得出矿工情绪监管与不安全行为的关系。矿工脱岗行为符合博弈论的基本特征,可以将演化博弈理论应用到矿工与煤矿企业的策略选择中去,因此,本文基于演化博弈理论寻找矿工脱岗行为的原因,进而分析从根本上降低矿工脱岗概率的方法。
1 演化博弈
矿工在岗的稳定状态即矿工与煤矿企业在一定约束条件下的有限理性均衡博弈。因此做出如下假设:①博弈双方(煤矿企业,矿工);②博弈双方行为集合,A1={矿工脱岗,矿工在岗},A2={煤矿企业检查,煤矿企业不检查};③矿工收入W;④矿工脱岗行为导致事故的可能性为q,发生事故后脱岗矿工和企业的损失分别为L、B;⑤煤矿企业对脱岗矿工的处罚为H;⑥在岗矿工因脱岗矿工的影响,外部损失为K;⑦煤矿企业正常收入为S,检查矿工脱岗的成本为F。综合以上因素,建立两博弈方的收益矩阵(图1)。

图1 双方收益Fig.1 Benefit of two parts of game
假设矿工在岗概率为x,煤矿企业检查脱岗概率为y,则矿工脱岗与否的效用、平均期望、在岗的复制动态方程见式(1)。
τ在岗=y(W-K)+(1-y)(W-K)=W-K
τ脱岗=y(W-H-qL)+(1-y)(W-qL)=
W-yH-qL
τ平均=τ在岗x+τ脱岗(1-x)=
(1-x)(W-yH-qL)+x(W-K)
x(x-1)(K-qL-yH)
(1)
同理煤矿企业检查与否的效用、平均期望、检查的复制动态方程见式(2)。
π不检查=xS+(1-x)(S-qB)
π检查=x(S-F)+(1-x)(H+S-F-qB)
π平均=yπ检查+(1-y)π不检查

(2)
命题1:当K=qL+yH,即矿工外部损失与矿工脱岗损失期望、矿工被检查处罚的期望之和相等时,无论矿工是否脱岗获得的收益都是一样的,所以矿工无论脱岗与否均为稳定状态。当K>qL+yH,即矿工外部损失大于矿工损失期望与矿工被检查处罚的期望之和时,x=0即矿工为获取最大的收益而采取脱岗行为,而后达到稳定状态;当K 命题2:当F=(1-x)H,即煤矿企业检查脱岗成本与矿工脱岗被处罚期望相等,无论煤矿企业是否检查脱岗企业获得的收益都是一样的,所以无论企业是否检查均为稳定状态。F>(1-x)H,即煤矿企业检查脱岗成本大于矿工脱岗被处罚期望,y=0即煤矿企业为避免过大的检查成本而采取不检查措施为稳定状态;F<(1-x)H,即煤矿企业检查脱岗成本小于矿工脱岗被处罚期望,y=1,即煤矿企业成本可通过对矿工的处罚来弥补而采取检查脱岗措施为稳定状态。 综上分析可知,矿工与煤矿企业选择是动态变化的一个过程,矿工在岗概率x与煤矿企业检查概率y双向影响,且二者稳定状态由惩罚力度F、在岗外部损失K、事故发生后矿工损失L、检查成本F等因素共同决定。 命题3:依据上述分析,矿工和煤矿企业博弈存在相关影响,为进一步分析建立系统,见式(3)。 (3) 系统平衡点有A点(脱岗,不检查)、B点(脱岗,检查)、C点(在岗,不检查)、D点(在岗,检查)、E点((H-F)/H,(K-qL)/H)。各假设条件的多样性导致平衡点E的不确定性。考虑E点在坐标轴中位置的各种情况,分析可知系统最终收敛于A点、B点、C点,即博弈双方演化过程的稳定点为A点(脱岗,不检查)、B点(脱岗,检查)、C点(在岗,不检查)。 某煤矿共有矿工约200人,矿工年收入为8万元,煤矿收益为每年15 000万元,煤矿企业检查脱岗成本为15万元,依据式(4)可得出脱岗导致事故先验概率的极大似然估计值是0.08,且事故总损失为1 000万元,该矿管理方式以惩罚为主,对于脱岗矿工的罚金为30万元。综合以上分析可确定各假设条件(单位:万/a):W=8,q=0.08,L=150,H=30,K=10,S=15 000,F=15,B=1 000。此时平衡点E点为(0.5,-0.07),由上述参数可得博弈双方收益见图1,其中-2>-4,因此矿工选择在岗时收益大,在此条件上,15 000>14 985,即煤矿企业选择不检查的收益最大,此系统最终收敛于(不脱岗,不检查)。 k=1,2,…K (4) 式中:I(yi=ck)指示函数,yi=ck为真,输出1,yi=ck非真,则输入0。 从演化规律来看,矿工在岗概率x与平衡点E横坐标存在两种关系。 1) 当x>E点横坐标时,以0.55为起点,0.75为终点,步长为0.05,取不同的x值。 (5) 将x分别代入式(5)并积分,可以得出x不同取值下煤矿企业检查脱岗概率随时间变化曲线。由图2可以看出,x>0.5(E点横坐标)时,煤矿企业刚开始检查脱岗,但矿工脱岗概率较低,设置脱岗检查实属浪费资源,经过长期博弈,煤矿企业会逐渐趋于不检查。此外可以看出矿工脱岗的概率越大时,即x越小,煤矿企业收敛于不检查的速度就越慢;矿工在岗的概率越大时,即x越大,煤矿企业就能在短时间内达到不检查的稳定状态;可见对于矿工脱岗的不同概率值,演化博弈趋向稳定的速度也不同。 2) 当x 将x分别代入式(5)并积分,可以得出x不同取值下煤矿企业检查脱岗概率随时间变化曲线。由图3可以看出,x<0.5(E点横坐标)时,脱岗情况严重,大部分矿工选择脱岗,这对企业的正常运营产生严重的影响,煤矿企业会从刚开始的不检查逐渐趋于检查,以减小矿工脱岗行为的发生。此外可以看出矿工脱岗的概率越大时,即x越小,则煤矿企业趋向于检查脱岗所用的时间就越短;矿工在岗的概率越大时,即x越大,则煤矿企业达到检查矿工脱岗的稳定状态所用的时间就越长;可见对于矿工脱岗的不同概率值,演化博弈趋向稳定的速度也不同。 图2 x>0.5时煤矿企业策略随时间变化关系Fig.2 Relationship between corporate strategy and time(x>0.5) 图3 x<0.5时煤矿企业策略随时间变化关系Fig.3 Relationship between corporate strategy and time(x<0.5) 3) 为了分析检查成本F、脱岗矿工处罚H分别对煤矿企业策略的影响,取x为0.5。F对煤矿企业策略影响:将案例H数值代入式(3)F(y),可知此系统平衡点为F=15,F分别取不同的值,代入式(3)F(y)并积分可得不同F值下煤矿企业检查脱岗概率随时间变化曲线。由图4(a)可知,当F值大于平衡点时,y最终趋于0,即当检查脱岗成本F过大时,煤矿企业为了节省成本倾向于不检查;而且随着检查成本F值的增大,倾向不检查所用的时间越短。由图4(b)可知,当F值小于平衡点时,y最终趋向于1,即当检查脱岗成本F不大时,煤矿企业为了防止脱岗情况的出现倾向于检查。随着检查成本的减小,倾向检查所用的时间越短。H对煤矿企业策略影响:将案例F数值代入式(3)F(y),可知此系统平衡点为H=30,H分别取不同的值,代入式(3)F(y)并积分可得不同H下煤矿企业检查脱岗概率随时间变化曲线。由图4(c)可知,当H值大于平衡点,y最终趋于1,即当对脱岗矿工的处罚H可以填补检查脱岗所需成本F值时,煤矿企业倾向于检查;H值越大,到达稳定状态所用的时间越短。由图4(d)可知,当H值小于平衡点,y最终趋向于0,即此时的H值不足以弥补检查带来的成本问题,为了节省资金倾向于不检查。H值越小,到达稳定状态所用时间越短。 图4 不同F值、H值时煤矿企业策略随时间变化关系Fig.4 Relationship between corporate strategy and time with different F value or H value 1) 将案例参数代入式(3)可得式(6)。由式(6)可知,y的取值对于dx/dt的正负无影响,以0.1为起点,0.9为终点,0.2为步长,取不同的y值。 (6) 将y分别代入式(6)并积分,可得y不同取值下矿工在岗概率x随时间变化曲线。由图5可知,不管煤矿企业检查概率是多少,矿工都是趋于在岗。煤矿企业检查力度越大,即y越大,矿工趋于在岗所用的时间就越短。 2) 为分析K对矿工策略的影响,取y=0.5。将q、L、y、H数值代入式(3)F(x),可知此系统平衡点为K=27,K取不同值代入式(3)F(x)并积分,得到不同K值下矿工策略随时间变化关系。由图6(a)可知,当在岗矿工因脱岗矿工影响其外部损失K过大时,x最终趋于0;即在岗矿工为了降低外部损失对自身的影响,而选择脱岗;且K越大,趋于稳态时间越短。由图6(b)可知,K不大时,在岗矿工可以忽略K对自身的影响,而选择坚守岗位;且K越小,矿工达到坚守岗位的稳态所用的时间越短。为分析L值对矿工策略的影响,取y=0。将q、K代入式(3)F(x),可知此系统平衡点为L=125,L取不同值代入式(3)F(x)并积分,得到不同L值下矿工策略随时间变化关系。由图6(c)可知,L值大于平衡点时,x最终趋于1,即矿工为了避免事故后过大的个人损失而选择在岗,而且L值越大,对矿工的“震慑”作用越大,达到在岗稳定状态所用时间越短。由图6(d)可知,L值较小时,x最终趋向于0,即较小的L值对矿工影响也较小,为获得较大收益,而选择脱岗。 图5 矿工策略随时间变化关系Fig.5 Relationship between miner strategy and time 图6 不同K值、L值时矿工策略随时间变化关系Fig.6 Relationship between miner strategy and time with different K value or L value 1) 由分析可知,上述实例中无论煤矿检查与否,矿工均趋于在岗,仅存在收敛速度的差别。其中起决定性作用的是K(10) 2) 煤矿企业还可以从降低外部影响K。本文分析以负向激励惩罚为主,煤矿企业应统计矿工在岗情况并归档,对于长期坚守在工作岗位的矿工进行奖励,即间接降低在岗矿工的外部性损失,矿工就会选择忽略外部性损失K,进而选择坚守岗位。 3) 在本案例中煤矿企业检查与否对矿工脱岗概率影响不大,但是当K>qL时,为了达到K 1) 矿工与煤矿企业演化博弈是一个动态的过程,可知矿工是否脱岗和煤矿企业检查概率y、外部影响K、脱岗引发事故概率q、矿工事故损失L、惩罚力度H等因素密切相关。 2) 对于最终收敛于A点(脱岗,不检查)的系统,这种稳定状态如果长期不打破的话,会威胁矿工的安全和煤矿企业的发展,双方需要及时改变策略。如煤矿企业可以从降低检查成本F和外部影响K入手,前者可以使得煤矿企业趋于检查,后者可以使得矿工趋于在岗。 3) 惩罚变量H的引入填补企业损失的缺口,也间接增加了不脱岗矿工收入,所以企业需要及时处理脱岗事故,以制止脱岗事故发生。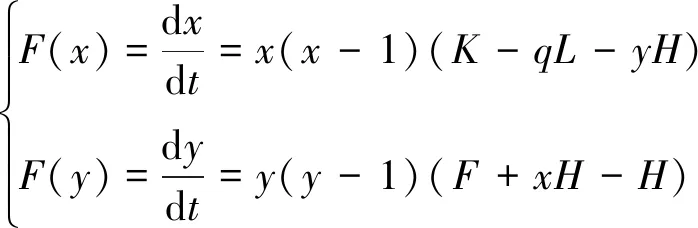
2 实例分析
2.1 案例概况
2.2 煤矿企业策略分析




2.3 矿工策略分析



3 改善措施
4 结 论

