基于AE-CNN的手势识别算法

付 优 任 芳

1(山西建筑职业技术学院计算机工程系 山西 晋中 030600)2(陕西师范大学数学与信息科学学院 陕西 西安 710061)

0 引 言

在机器学习领域中，深度学习是一个崭新的研究方向，其本质是一个具有多隐层的非线性网络模型：对大规模原始数据样本进行训练，然后通过网络模型对原始数据样本的特征进行提取，最终实现对原始数据进行预测或分类。

在计算机视觉和图像识别领域，卷积神经网络(CNN)取得了显著的成绩[1-3]。此外，深度学习广泛应用于数据挖掘、自然语言处理[4]、行人检测[5]、手势识别[6]和语音识别[7]等领域。与深度置信网络[8]、S层自动编码[9]等其他深度神经网络相比，CNN可以直接处理二维图像。当二维图像转换为一维信号时，会损失输入数据的空间结构特征，而通过CNN算法进行处理时可避免这种损失。因此，基于CNN的识别算法是目前流行的图像识别方法之一，并且其识别结果更加可靠。

手势识别是人机交互系统发展的一个重要领域。常见的手势识别方式很多，如：基于几何特征的识别方法通过提取手势的几何特征信息进行识别，具有良好的稳定性，但其不能通过提升样本量的同时进行识别率的提升[10]；基于隐马尔科夫模型的识别方法虽然具有描述手势时空变化的能力，但是该方法的识别速度却不尽如人意[11]。随着卷积神经网络在计算机视觉的迅速发展，卷积神经网络在手势识别上的应用有着突破进展，如：Takayoshi[12]在输入卷积网络之前讨论了预处理过程和手势识别过程的融合，实现了端到端手势识别，并使得手势识别率得到了提升；Barros等[13]创造性地使用立体声卷积核进行手势识别，获得了更好的手势识别识别率。虽然上述方法取得了良好的识别结果，但它们仍存在收敛速度慢、识别率低的问题。

为了进一步提高CNN的收敛速度，降低训练难度，本文提出了一种AE-CNN算法。通过对CNN的特征提取和分类过程的研究，分析分类错误的原因，最终提出了一种基于AE-CNN的手势识别算法。首先，通过神经网络的识别和连续迭代对特征残差进行特性提取；然后进行局部自适应增强；最后，特征参数通过隐层的反向反馈，进行有效地训练。同时，为了解决样本数量少的问题，本文提出了一种新的样本扩增方法，即通过对原样本进行平移、旋转、缩放和波纹形变等处理，增加了样本量。

1 基于AE-CNN的手势识别算法

1.1 前向过程分析

在CNN前向过程中，特征提取操作实现了卷积和池化效果。假设有m个卷积层，第i个输入特征为Mi，对应的卷积核为Ci。偏值为B1，激活函数为f，则卷积层的输出特征Fc表示为：

(1)

式中：con表示卷积函数。

对卷积输出特性进行池化操作，进一步减小维数；然后，通过对全连接层进行权值变换和激活，可获得分类结果。全连接层的分类函数可表示为：

Fo=f(WT+B2)

(2)

式中：T是完全连接层的输入特性；W是相应的权重；B2是偏差值。

1.2 反向过程分析

分类误差在CNN的反向过程中被传播到隐层，实现了卷积核和全连接矩阵权值与偏置的更新。更新后的参数用于下一次迭代的前向过程，因此CNN的迭代更新提高了识别率。假设步长为η，在CNN隐层中，权值ω和偏差b由ω1、b1更新为ω2、b2，更新函数如下：

ω2=ω1-η▽ω

(3)

b2=b1-η▽b

(4)

1.3 AE-CNN的算法实现

AE-CNN结构如图1所示。前向过程中包含了目标分类和提取特征。误差的反向反馈包含在反向过程中。输入数据经过前向处理后进行分类，获得分类结果。每个结果对应一个唯一的分类。输入数据真实属于的类别称为真值类别，真值类的对应值为1，另一个类的对应值为0。

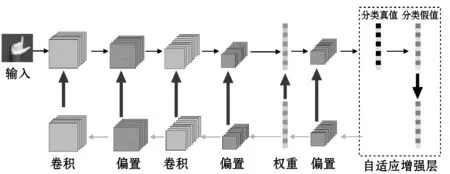
图1 AE-CNN的结构

在隐层中，目标误差函数E(ω,b)用于度量每个参数对输入数据的学习效果。为了使分类yi尽可能接近真值分类y′i，在CNN的前向与反向过程之间增加自适应增强模块。在增强模块中，对分类结果进行特征分析，然后通过调整增强系数对特征误差进行自适应地调整。最后，通过反向过程将增强后的特征误差反馈到隐层，达到降低目标错误函数输出和提升下一次分类效果的目的。当相近的两个误差输出不大于阈值时，则可以判断收敛和学习任务均已实现。关于一个n的分类问题，它的目标错误函数表示如下：

(5)

式中：j表示分类个数；err是其分类误差。根据梯度下降法，权值和偏值的梯度变化可表示为：

(6)

(7)

d=(yj-y′j)f′=errj·f′

(8)

式中：d是剩余值；x是输入特性中的值；f′是激活函数f的导数。

2 算法步骤

基于AE-CNN手势识别算法的步骤为：

1) 分类误差的计算。分类结果通过CNN的前向处理得到，然后将分类真值与分类结果进行对比，可计算得出分类误差。

2) 分类结果特征的提取。分析输出层分类结果，将分类结果的两个最大值设为特征值。

3) 计算增强系数。增强系数是由基于迭代的时间和前向的分类结果计算得到。若分类正确，则与分类特性对应的错误值将增加α1倍。相反，当分类错误时，其会增加α2倍。因此，自适应增强系数α可以表示为：

(9)

式中：k是乘积系数；g是当前迭代的时间；θ是修正系数；c是常数。根据不同的数据集，用式(9)计算α1和α2的值。

4) 自适应增强分类特征对应的误差值。假设err是分类特性的错误值，s是大小写正确分类中的标志。此时，增强函数err′s由下式计算得到：

err′s=αs·errs

(10)

5) 增强残差的计算。增强残差包括剩余误差的残差和特征误差后的残差，由式(8)表示。

6) 将增强后的残余反馈给隐层。在隐层中，权值和偏差按式(6)和式(7)计算。

7) 更新模型。最后利用式(3)和式(4)中的函数更新隐层的权值和偏差。

3 实 验

在实验部分，将从算法的收敛性能、识别率和训练时间三个方面对本文算法进行验证。

3.1 实验设置

实验采用了Jochen Triesch数据库(JTD)。这个数据库包含10个手势，来自24个不同背景的人，一个亮的，一个暗的，在复杂背景前完成的。所有图片的大小为128×128,并集中在手势。JTD数据库的示例如图2所示。

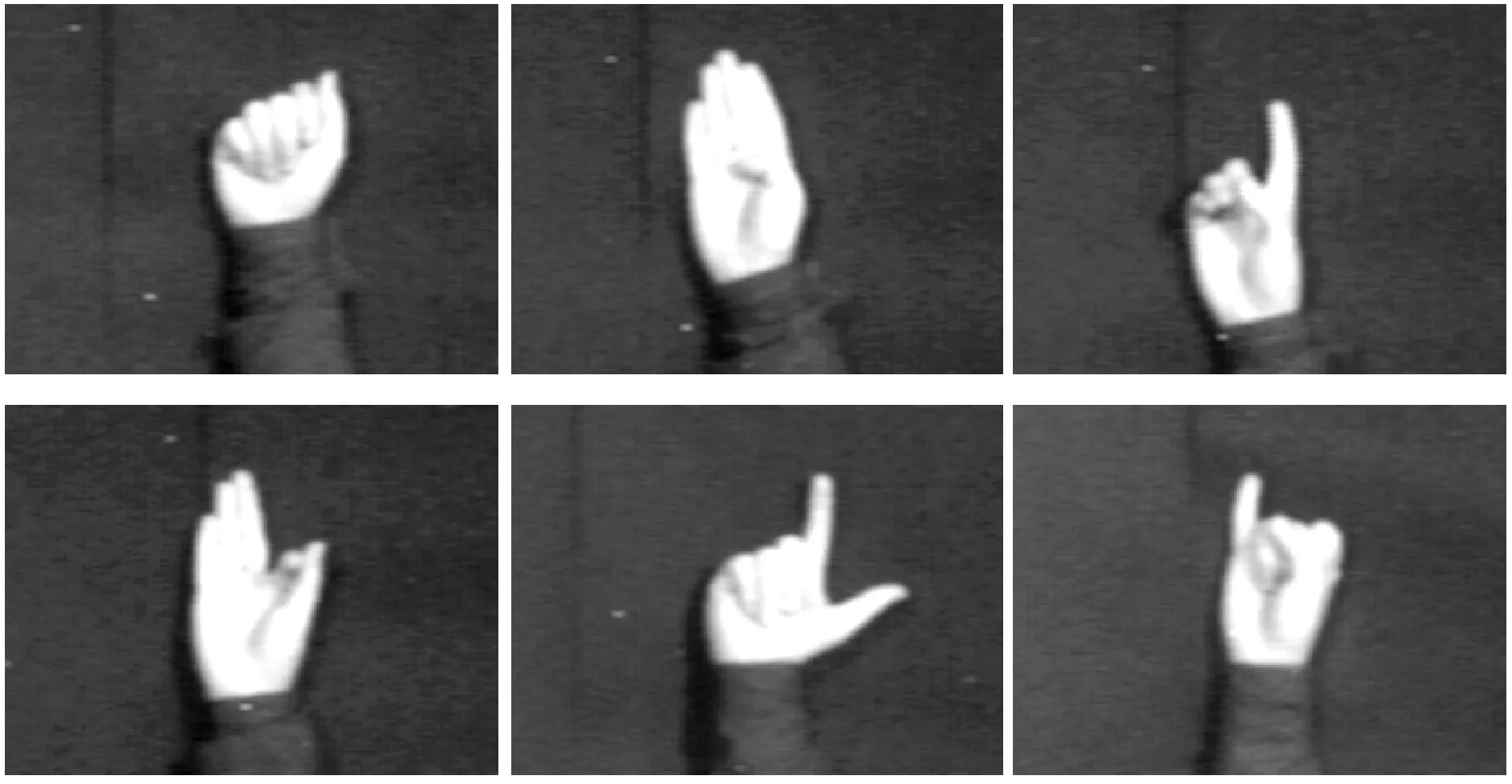
图2 实验所用的的手势示例

在样本集上执行二进制处理和边界删除。最后，大小统一为28×28像素。CNN采用随机梯度下降算法。在两个卷积层中，卷积核的个数分别设为6和72。其他参数设置如表1所示。

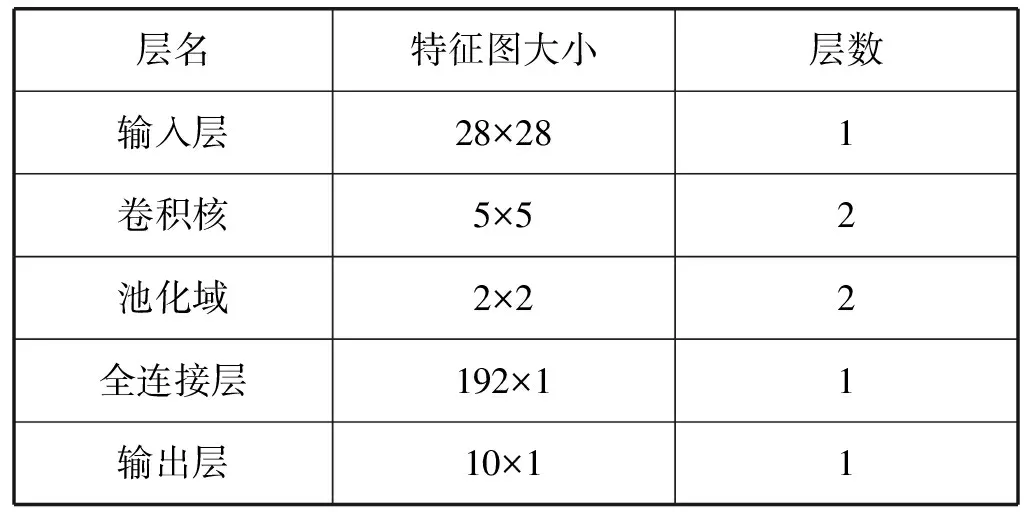
表1 卷机神经网络参数

实验中使用的自适应增强系数为α1、α2，表达式如下：

(11)

(12)

(13)

(14)

式中：g是迭代时间；θ1、θ2是相应的修正函数。

3.2 样本扩充方法

深度学习训练需要大量的样本进行训练，在样本容量缺乏的情况下，通常需要人为地增加训练样本的数量。常用的增强方法有弹性变形、噪声和仿射变换等。在不改动手势结构关系的基础上，提出了一种结合平移、旋转和缩放的波形扭曲的方法，从而实现对训练样本量的扩充。

3.3 对比实验

1) 收敛性能对比。原始CNN算法和本文算法的收敛曲线如图3所示。结果表明，原始算法的收敛性指数和算法的收敛性均随训练频率的增加而降低，并在第60次迭代中实现了收敛。因此通过对比收敛曲线可得知，本文算法在迭代过程中收敛速度快于原算法，并且收敛效果较好。

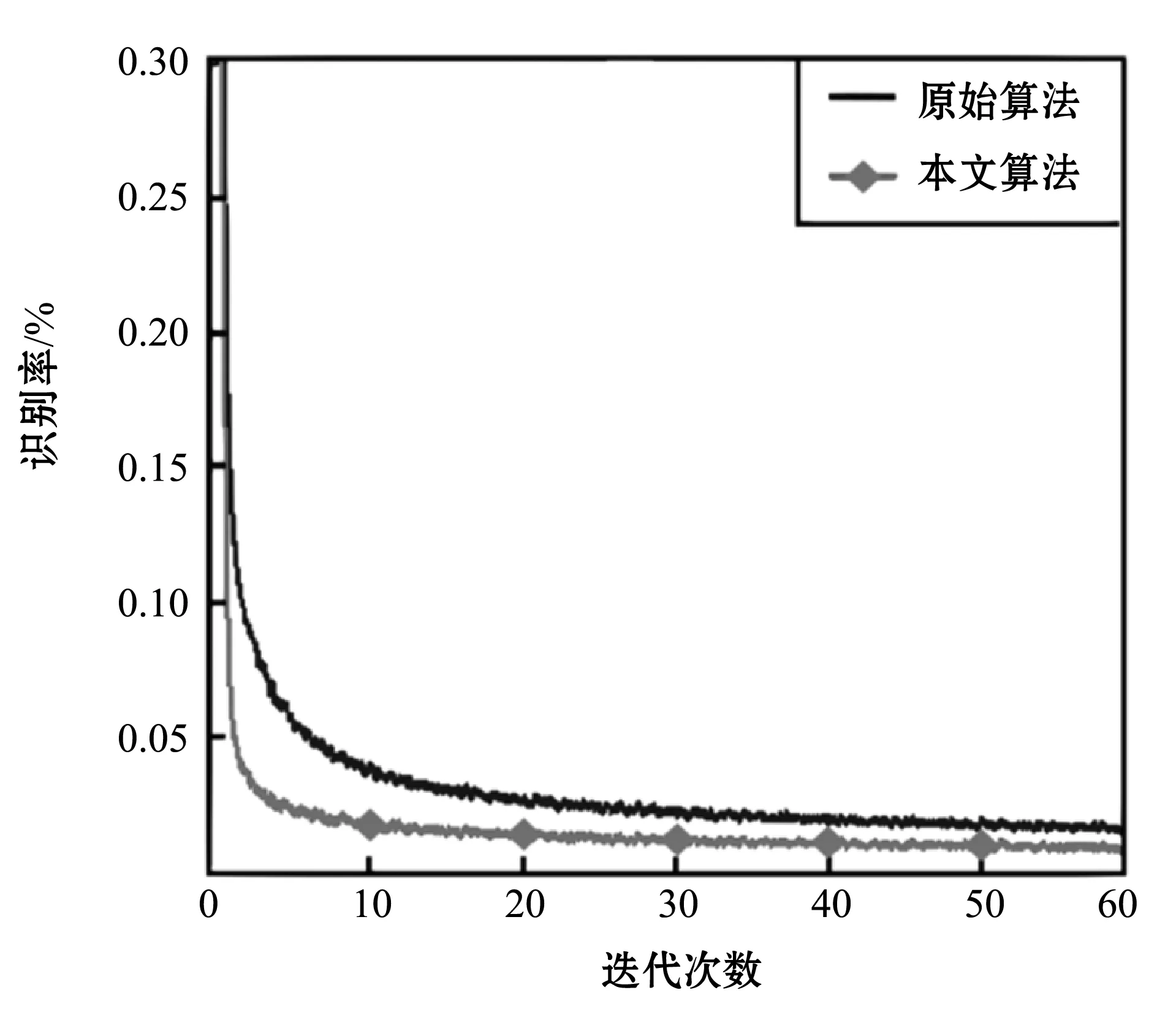
图3 原始CNN算法和本文算法的收敛曲线

2) 识别率对比。将所提出的算法与深度神经网络模型[14]中的多尺度梯度进行比较，得到的识别率如表2所示。文献[14]中使用的特征分别为一般梯度特征、多尺度梯度特征、多尺度Gabor特征要点、梯度取向直方图(HOG)以及局部二值模式(LBP)。分类器都是5层CNN。从表2中可以看出，与其他几种方法相比，本文算法的识别率得到了提高。

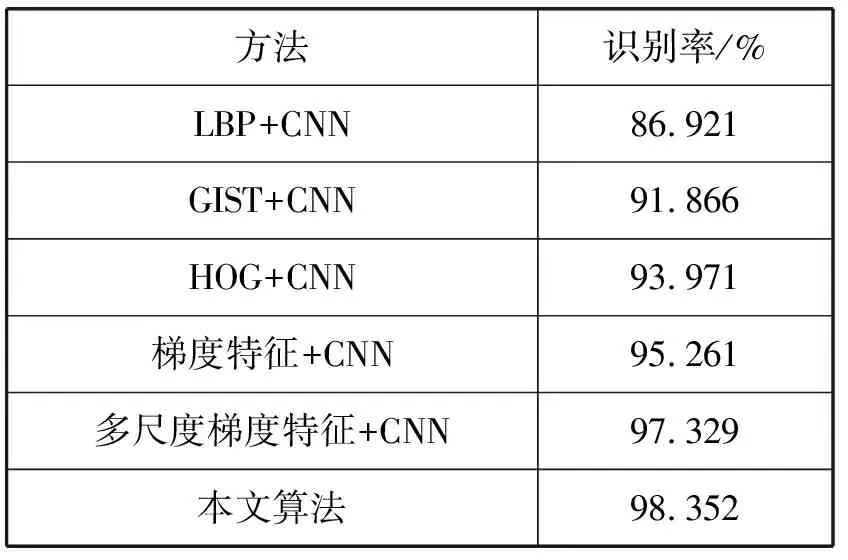
表2 不同算法识别率对比

为了加强检验算法的鲁棒性和稳定性，随机选取20个字符作为一组样本，执行4次，得到另外4组样本。然后对另外4组样本进行实验。表3所示为识别率结果，可以看出，不同样本集的识别结果是稳定的，因此提出的算法具备较强的鲁棒性。

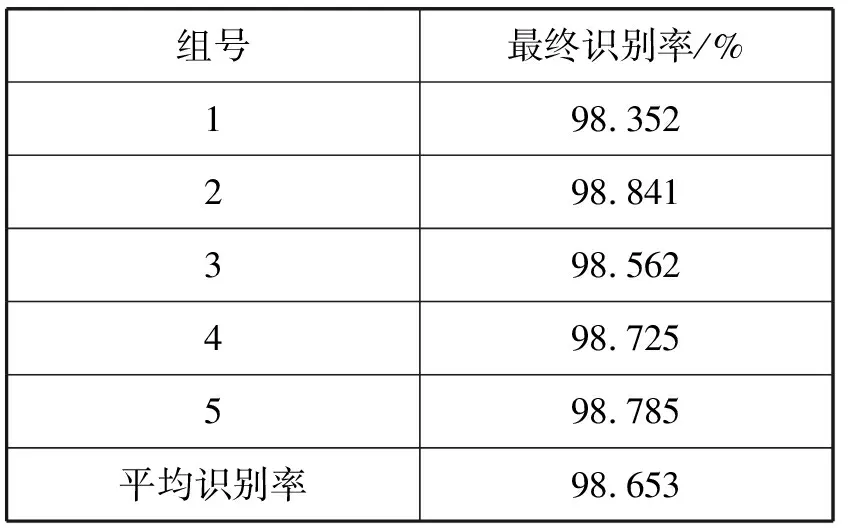
表3 多组样本情况下的识别率

3) 训练时间对比。对于5组样本，分别计算原始CNN算法和本文提出算法的训练时间。由表4可以看出，原来的CNN算法和本文提出的算法训练时间几乎是一样的，其时间差异小到可以忽略不计。

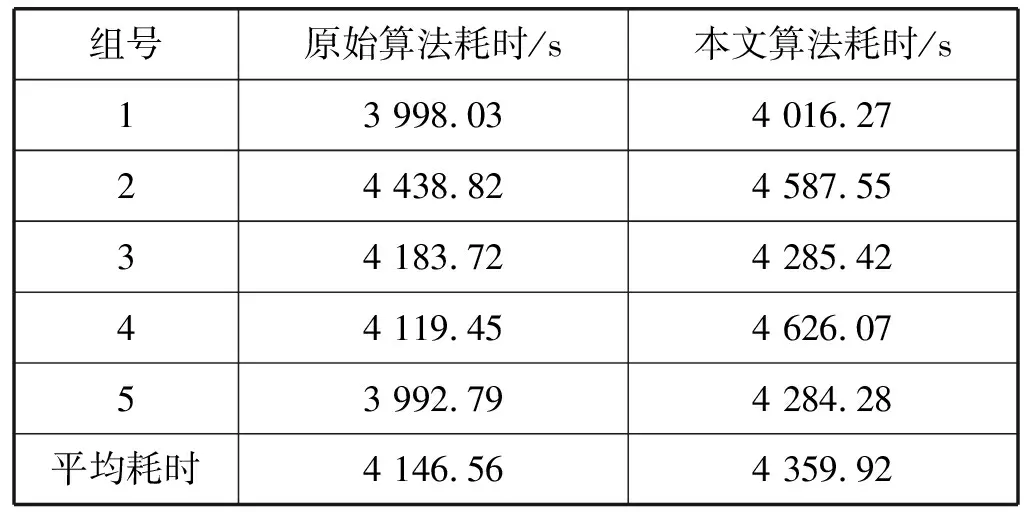
表4 多组样本情况下的训练耗时

4) 样本扩增实验。为了验证样本扩增试验的性能，对上述5组数据进行样本扩增。该算法的平均识别率和平均训练时间如表5所示。可以看出，样本扩增已延长了一定的训练时间，但它对识别率的贡献更为重要。因此，样本增强是深度学习模型训练的必要步骤。

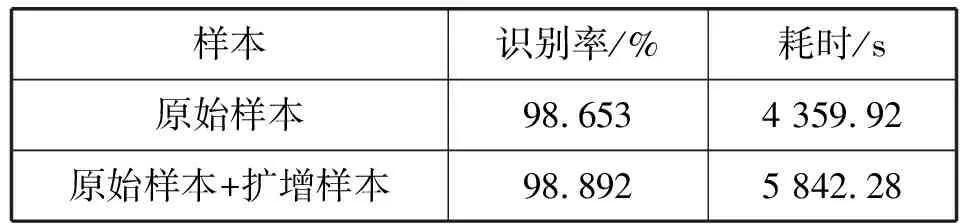
表5 样本扩增实验结果

4 结 语

通过对CNN训练过程中误差产生的原因及其反馈模型进行分析，提出了基于AE-CNN的手势算法。实验结果表明，本文算法收敛速度快、识别准确率高，并且没有明显增加识别过程的耗时性。另外，为处理样本量缺乏的难题，本文提出了一种基于波形扭曲的样本量扩增方法，进一步提高本文算法的识别率。