加性与广义加性模型回归分析
胡良平
(1.军事科学院研究生院,北京 100850;2.世界中医药学会联合会临床科研统计学专业委员会,北京 100029 *通信作者:胡良平,E-mail:lphu812@sina.com)
1 概 述[1-2]
1.1 加性模型
将多重线性回归模型进行推广,使其表达式成为下面的式(1)形式:

在式(1)中,sj(Xj),j=1,2,…,p,是 P个“光滑函数”;误差“ε”满足如下条件:它的期望为0[E(ε)=0]、方差为 σ2[Var(ε)=σ2]。为了使式(1)成为可以估计的,要求光滑函数 si(Xi)必须满足如下的标准化条件:即期望为 0,E[sj(Xj)]=0。式(1)中的P个光滑函数不以参数形式呈现,而以非参数形式呈现。
1.2 广义加性模型
在加性模型式(1)中,假定因变量y服从正态分布。然而,在很多场合下,因变量不服从正态分布,而可能服从其他某种分布。现假定式(1)中的因变量y具有下面的指数族分布密度,见式(2):
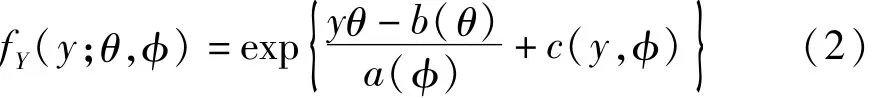
在式(2)中,θ被称为“自然参数”,φ被称为“尺度参数”;以因变量y的平均值μ为自变量构造出的函数 g(μ)被称为“连接函数”,它与协变量“X1、X2、…、Xp”之间建立了关系。下面的数量定义了“加性分量(或成分)”,见式(3):

式(3)中,S1()、S2()、…、Sp()都是“光滑函数”。μ与η之间的关系由下式来定义:

最常用的连接函数为“典型连接函数”,即η=θ。
1.3 加性与广义加性模型回归分析应用的场合
广义线性模型强调对模型中参数的估计和推断,而广义加性模型则聚焦于如何用非参数法探测数据。换言之,广义加性模型更适合于探查数据并可视化因变量与自变量之间的关系。
1.4 加性与广义加性模型回归分析的计算原理
1.4.1 加性模型回归分析的计算原理
基于加性模型式(1),可以构造如下的残差,见式(5):

式(5)被称为“第k项光滑参数与因变量y”之间的“残差”,即 Rk≈sk(Xk)。严格地说,应该有下式成立,见式(6):

由式(5)可知:对于所有其他的项“j”(j≠k),在给定“{s^j(),j≠k}”的估计值时,其观测值提供了一种用于估计每个光滑函数“sk()”的方法。依此做法求得结果的迭代过程被称为“后退拟合算法”,此法最早由Friedman和Stuetzle提出。
1.4.2 后退拟合算法
1.4.2.1 未加权的后退拟合算法
未加权的后退拟合算法步骤如下:
第1步:初始化。

第2步:迭代。令 m=m+1;让 j从1到 p循环,循环体内的计算公式为:
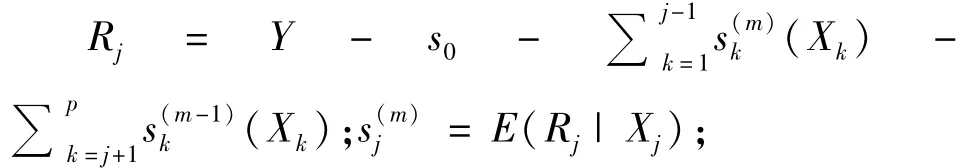
第3步:终止。

直到上式的计算结果不再下降,或满足收敛的临界值,就停止迭代。
值得注意的是:对于除正态分布之外的其他分布而言,具有权重的数值不稳定可能会引起收敛问题。即使当算法收敛时,各个个体函数并不需要彼此完全不同,即便对于同一个拟合曲面来说,由于协变量之间的依赖性会导致多于一个表达式出现。
1.4.2.2 加权的后退拟合算法
除了要对光滑器进行加权之外,加权的后退拟合算法具有与未加权的后退拟合算法相同的形式。在SAS的GAM过程步中,具体是在采用“局部计分过程”中且资料为非正态分布时,使用了“权重”。
GAM过程使用下面的“条件”作为后退拟合算法的“收敛临界值”:

此处,ε=10-8是缺省的界值。用户可以通过修改模型语句中的选项“EPSILON=”来改变此界值。
1.4.3 广义加性模型回归分析的计算原理
广义加性模型回归分析的计算原理比前面介绍的加性模型回归分析的计算原理稍复杂,其中,最关键的内容为“局部计分算法”。该算法的重要内容取决于与每个特定分布对应的“连接函数”。它们之间的关系见表1。

表1 局部计分算法涉及到的重要内容
由表1可知:一旦分布被指定,相应的“那些量”也就被定义了。于是,可按下面的步骤实施“局部计分算法”。
1.4.4 一般的局部计分算法
第1步:初始化。
si=g[E(y)],s01=s02=… =s0p=0,m=0
第2步:迭代。令m=m+1;从前一次迭代中获得各变量的相应数值,这些变量分别是:预测量η、均值μ、权重w和校正后的因变量z:

第3步:终止。直到达到收敛临界值或离差不再减少时,停止迭代。这里所说的“离差”,实际上是广义线性模型中“RSS”的一个扩展或推广。
GAM过程使用下面的“条件”作为局部计分算法的“收敛临界值”:

此处,ε=10-8是缺省的界值。用户可以通过修改模型语句中的选项“EPSILON=”来改变此界值。
算法小结:广义加性模型的估计过程由两个循环构成。在局部计分算法(外循环)每一步内部,使用加权后退拟合算法(内循环),直到收敛或RSS不再减少。然后,基于来自这个加权后退拟合算法得到的估计量,计算出一组新的权重,开始计分算法的下轮迭代。当达到收敛临界值或估计量的离差停止下降时,计分算法也就停止了。
2 基于加性模型回归分析解决实际问题[2]
2.1 问题与数据结构
【例1】下面是一个假设的来自化学试验的例子:每次试验,研究者将某种催化剂加入到某种化学溶液中,从而合成一种新化合物。其数据是测量溶液的温度(temperature)、加入的催化剂量(catalyst)和化学反应量(yield)的结果。试验数据的结构很简单,两个计量原因变量和一个计量结果变量及其取值,前6次试验数据见表2。

表2 不同“溶液温度”和“催化剂量”条件下化学反应量的测定结果
【对数据结构的分析】对于每次试验而言,可以观测到3个计量的数据,即溶液的温度(temperature)、加入的催化剂量(catalyst)和化学反应的量(yield)。
【统计分析方法的选择】若希望考察化学反应的量(yield)是如何随溶液的温度(temperature)和催化剂量(catalyst)变化而变化的依赖关系,可选择多重线性回归分析。因本例中的因变量为计量变量,故可以考虑选用“加性模型回归分析”。若因变量是定性变量或计数变量,就可能需要选用“广义加性模型回归分析”。因篇幅所限,本文只介绍如何用SAS实现“加性模型回归分析”。
2.2 基于常规方法构建多重线性回归模型[3-4]
2.2.1 创建SAS数据集
创建一个名为“ExperimentA”的临时SAS数据集所需的数据步程序:data ExperimentA;
format Temperature f4.0 Catalyst f6.3 Yield f8.3;
input Temperature Catalyst Yield@@;
x1=temperature;x2=Catalyst;y=Yield;
datalines;
80 0.005 6.039 80 0.010 4.719 80 0.015 6.301
80 0.020 4.558 80 0.025 5.917 80 0.030 4.365
80 0.035 6.540 80 0.040 5.063 80 0.045 4.668
80 0.050 7.641 80 0.055 6.736 80 0.060 7.255
80 0.065 5.515 80 0.070 5.260 80 0.075 4.813
80 0.080 4.465 90 0.005 4.540 90 0.010 3.553
90 0.015 5.611 90 0.020 4.586 90 0.025 6.503
90 0.030 4.671 90 0.035 4.919 90 0.040 6.536
90 0.045 4.799 90 0.050 6.002 90 0.055 6.988
90 0.060 6.206 90 0.065 5.193 90 0.070 5.783
90 0.075 6.482 90 0.080 5.222 100 0.005 5.042
100 0.010 5.551 100 0.015 4.804 100 0.020 5.313
100 0.025 4.957 100 0.030 6.177 100 0.035 5.433
100 0.040 6.139 100 0.045 6.217 100 0.050 6.498
100 0.055 7.037 100 0.060 5.589 100 0.065 5.593
100 0.070 7.438 100 0.075 4.794 100 0.080 3.692
110 0.005 6.005 110 0.010 5.493 110 0.015 5.107
110 0.020 5.511 110 0.025 5.692 110 0.030 5.969
110 0.035 6.244 110 0.040 7.364 110 0.045 6.412
110 0.050 6.928 110 0.055 6.814 110 0.060 8.071
110 0.065 6.038 110 0.070 6.295 110 0.075 4.308
110 0.080 7.020 120 0.005 5.409 120 0.010 7.009
120 0.015 6.160 120 0.020 7.408 120 0.025 7.123
120 0.030 7.009 120 0.035 7.708 120 0.040 5.278
120 0.045 8.111 120 0.050 8.547 120 0.055 8.279
120 0.060 8.736 120 0.065 6.988 120 0.070 6.283
120 0.075 7.367 120 0.080 6.579 130 0.005 7.629
130 0.010 7.171 130 0.015 5.997 130 0.020 6.587
130 0.025 7.335 130 0.030 7.209 130 0.035 8.259
130 0.040 6.530 130 0.045 8.400 130 0.050 7.218
130 0.055 9.167 130 0.060 9.082 130 0.065 7.680
130 0.070 7.139 130 0.075 7.275 130 0.080 7.544
140 0.005 4.860 140 0.010 5.932 140 0.015 3.685
140 0.020 5.581 140 0.025 4.935 140 0.030 5.197
140 0.035 5.559 140 0.040 4.836 140 0.045 5.795
140 0.050 5.524 140 0.055 7.736 140 0.060 5.628
140 0.065 6.644 140 0.070 3.785 140 0.075 4.853
140 0.080 6.006
;
run;
【SAS程序说明】数据中每行上有3次试验的结果,每次试验结果都有3个数据,即温度数值(temperature)、催化剂量(catalyst)与产量(yield)。
创建一个名为“ExperimentB”的临时SAS数据集的SAS数据步程序:
data ExperimentB;
set ExperimentA;
x3=x1*x1;x4=x2*x2;x5=x1*x2;x6=x3*x1;
x7=x4*x2;x8=x3*x2;x9=x4*x1;
run;
【SAS程序说明】以上SAS程序产生7个“派生变量”,它们分别为x1与x2两个原始自变量的平方项、立方项、交叉乘积项,具体地说,x3=x21、x4=x22、x5=x1×x2、x6=x31、x7=x32、x8=x21×x2、x9=x22×x1。其中,由前面的SAS程序可知:x1=temperature、x2=Catalyst、y=Yield。
2.2.2 基于常规方法构建多重线性回归模型
利用下面的两个SAS过程步程序可以创建两个二重线性回归模型:
proc reg data=ExperimentA;
model y=x1 x2/r;
run;
记以上SAS程序创建的二重线性回归模型为模型(1)。
proc reg data=ExperimentA;
model y=x1 x2/noint r;
run;
记以上SAS程序创建的二重线性回归模型为模型(2)。
经比较,模型(1)优于模型(2)。具体方法详见下文,此处从略。
引入自变量的“二次项”,利用下面的两个SAS过程步程序可以创建两个多重线性回归模型:
proc reg data=ExperimentB;
model y=x1-x5/selection=backward sle=0.05 r;
run;
记以上SAS程序创建的多重线性回归模型为模型(3)。
proc reg data=ExperimentB;
model y=x1-x5/noint selection=backward sle=0.05 r;
run;
记以上SAS程序创建的多重线性回归模型为模型(4)。
经比较,模型(4)优于模型(3)。具体方法详见下文,此处从略。
引入自变量的“三次项”,利用下面的两个SAS过程步程序可以创建两个多重线性回归模型:
proc reg data=ExperimentB;
model y=x1-x9/selection=backward sle=0.05 r;
run;
记以上SAS程序创建的多重线性回归模型为模型(5)。
proc reg data=ExperimentB;
model y=x1-x9/noint selection=backward sle=0.05 r;run;
记以上SAS程序创建的多重线性回归模型为模型(6)。
经比较,模型(5)优于模型(6)。具体方法详见下文,此处从略。
将模型(4)与模型(1)比较,得出模型(4)优于模型(1)。最后,需要将模型(5)与模型(4)作比较,具体方法如下:
模型(4)的有关信息为:SSε=128.48055(模型误差的离均差平方和)、dfε=108(误差的自由度);
模型(5)的有关信息为:SSε=78.07028(模型误差的离均差平方和)、dfε=106(误差的自由度)。
利用下面的F检验对上述回归模型(5)与模型(4)进行拟合优度比较:

对应的 F临界值 F((2,106)(0.01))<4.82,因 F=34.222>4.82,说明P<0.01,故需要选择参数多的回归模型(5)。模型(5)的输出结果如下:

根据最后的“参数估计值”,请读者写出相应的“五重线性回归模型”的表达式,此处从略。
2.3 基于加性模型构建多重回归模型[2]
利用下面的SAS程序可基于加性模型构建多重回归模型:
proc gam data=ExperimentA;
model y=spline(x1)spline(x2);
output out=a3 residual;
run;
【SAS程序说明】以上SAS程序调用GAM过程拟合加性模型。模型语句等号右边的两项分别用“三次样条函数”拟合自变量x1与x2。
【SAS输出结果及其解释】
因变量:y
平滑模型成分:spline(x1)spline(x2)
输入数据集的汇总
观测数 112
缺失观测数 0
分布 Gaussian
关联函数 Identity
以上是关于数据集一般情况的描述,并告知:假定因变量y服从正态分布(或高斯分布)、采用恒等的关联函数,实际上,就是没有对y作任何变量变换。

迭代汇总和拟合统计量
以上是关于“迭代汇总和拟合统计量”的信息,关键是倒数第二行:最终估计的偏差为68.464846,此值相当于通常回归分析给出的“模型误差的离差平方法和”。

回归模型分析
以上给出的是“加性模型”中“参数分析部分”的结果,即

平滑模型分析
以上给出的是“加性模型”中“非参数分析部分”的结果,即

将模型(7)与模型(8)合并成一个模型,见模型(9):


平滑模型分析
以上是关于加性模型中两个非参数项(即样条函数)的假设检验结果,两项各占用了3个自由度,经卡方检验,说明两个非参数项都具有统计学意义。
图1左边的曲线描述的是模型(8)中的第1项;图1右边的曲线描述的是模型(8)中的第2项。其中,第1项比第2项更复杂。

图1 两个非参数项分别与x1、x2之间的函数曲线
2.4 两类回归模型拟合效果比较
常规多重线性回归模型与加性多重回归模型对同一个资料究竟谁的拟合效果更好?这个问题尚无公认的评判方法,但可以近似地采用下面的方法进行比较:
将常规多重线性回归模型中拟合效果最好的模型(5)与加性模型(9)进行比较,用类似于模型(5)与模型(4)比较的F检验:
已知:模型(9)的 SSε=68.464856、dfε=103;模型(5)的 SSε=78.07028、dfε=106。利用下面的SAS程序可以求出检验统计量F的数值以及对应的F临界值:data abc;
v1=(78.07028-68.464856)/(106-103);
v2=68.464856/103;
F=v1/v2;
F3_103=FINV(0.95,3,103);proc print data=abc;
var F F3_103;
run;
【SAS输出结果】
Obs F F3_103
1 4.81687 2.69284
因 F=4.817>F(3,103)(0.95)=2.693,所以,P<0.05,说明不能用含参数个数少的模型(5)取代含参数个数多的模型(9)。
【结论】本例以加性模型的回归分析结果为优。
——与非适应性回归分析的比较

