光学测绘卫星星地相机夹角在轨实时定标方法

蒋唯娇，刘 薇，钱方明,3，王 慧，王柯俨

(1.西安电子科技大学 综合业务网国家重点实验室，陕西 西安 710071；2.西安测绘研究所 地理信息工程国家重点实验室，陕西 西安 710054；3.中国人民解放军信息工程大学，河南 郑州 450002)

在卫星摄影测量中，地相机的外方位角元素是影响定位精度，尤其是无地面控制点定位精度的关键因素之一[1]。通常利用星地相机主光轴之间夹角转换关系，将星相机所测量的姿态转换为地相机的外方位角元素。但由于卫星在轨运行期间受到各方复杂因素的影响，例如压力、振动、温度等，导致星地相机夹角、星相机测量数据都不可避免地含有系统性误差及随机误差，直接影响外方位角元素精度。笔者依据天绘一号卫星长期积累的大量实测数据和理论研究，对星相机的测量误差以及星地相机夹角在轨定标结果进行了分析，发现热弹性形变误差是造成星地相机主光轴夹角发生变化的最主要因素，制约了定位精度。

针对上述问题，目前的方法主要分为两类：一类是利用硬件设计提升星地相机整体热稳定性，具体为在载荷研制时对结构进行优化设计、采用耐高温材料[2]，但受限于当前工艺制造水平以及温度控制水平，这类方法对定位精度的提升有限；另一类是基于地面定标场的摄影测量标定方法，具体为在地面布设检校场，根据卫星过顶时拍摄的像片，利用摄影测量原理求解星地相机主光轴夹角变化[3]，但由于现有技术下星地相机夹角姿态稳定度不高、定标周期过长，随着卫星定位精度要求的提升，这类方法难以满足高精度测绘需求。因此，需要对星地相机主光轴夹角变化进行实时高精度的标定。

笔者提出一种可在星上实现的光学测绘卫星相机夹角实时定标方法。该方法是在星相机、地相机光学系统内部合理加装光学自准直部件，有效地利用相机原有光路，将各自相机主光轴的变化转化为光斑影像位置的变化，便可解算出相机之间夹角的变化，实现快速、高效的星上实时定标。

1 星地相机姿态测量原理

1.1 星相机姿态测量原理

星相机是一种用于测定卫星三轴瞬时姿态的高精度空间姿态测量设备。它以恒星为参照物，利用实际拍摄到的恒星影像来计算星相机在惯性坐标系中的瞬时指向，再根据星地相机之间的夹角确定地相机的外方位角元素。星相机工作主要分为星点提取[4]、星图识别[5]、姿态计算[6-7]等步骤，具体如图1所示。

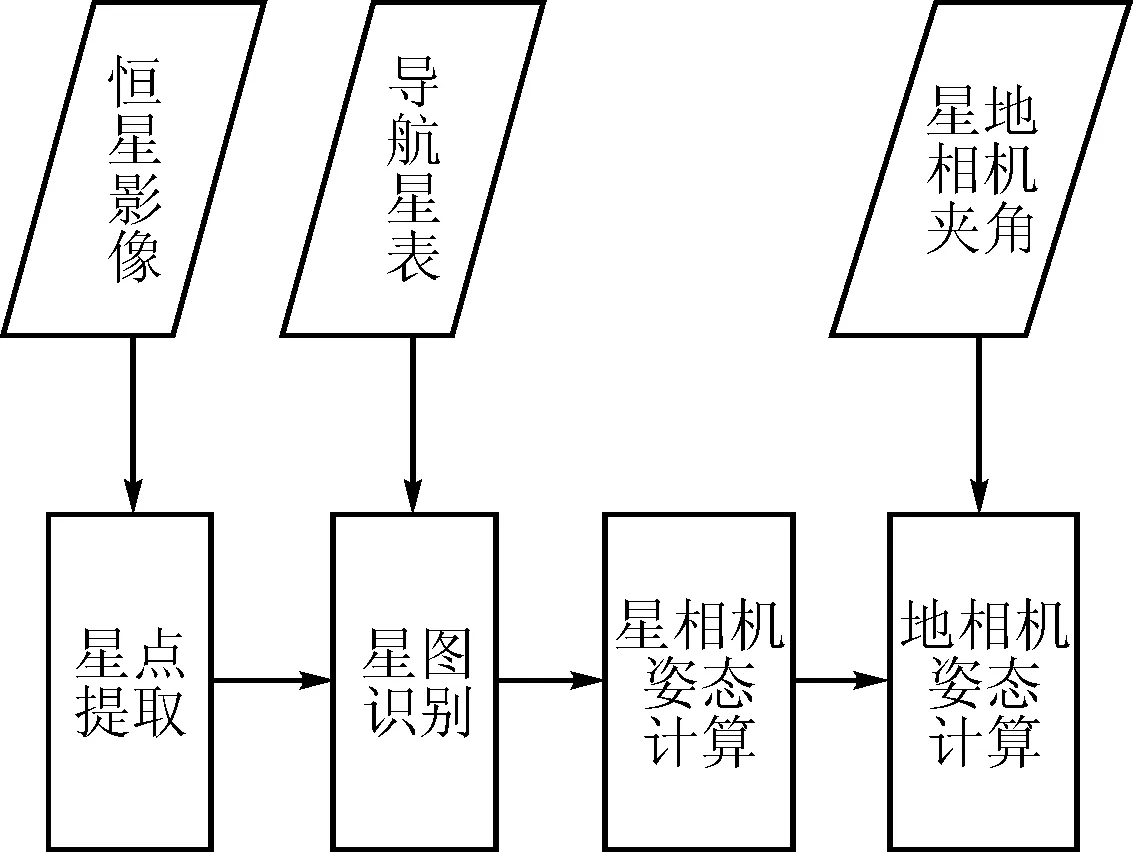
图1 星相机测量原理

图2 星相机和地相机主光轴夹角示意图

1.2 地相机外方位角元素计算

星相机测量的姿态数据是星相机测量坐标系相对于惯性坐标系的姿态，利用星地相机之间的夹角建立星相机测量坐标系与地相机测量坐标系的转换关系，从而计算当前地相机相对于惯性坐标系的姿态。星地相机主光轴夹角示意如图2所示。其中，Os-XsYsZs为星相机测量坐标系，Ot-XtYtZt为地相机测量坐标系，(φ,ω,κ)为星相机和地相机主光轴夹角，φ为俯仰角，ω为横滚角，κ为偏航角。因此，星相机测量坐标系在地相机测量坐标系中的转换矩阵 (服从Z-X-Y转序)可以表示为

(1)

根据星相机测量坐标系在地相机测量坐标系中的转换矩阵以及星相机测量坐标系在惯性坐标系中的旋转矩阵，可以计算地相机测量坐标系在惯性坐标系的旋转矩阵：

(2)

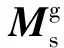
由此可以计算得到地相机外方位角元素(αt,βt,γt)：

(3)

2 星地相机夹角误差分析

选取天绘一号02星稳定运行后的星相机测量数据和基于试验场定标的星地相机主光轴夹角标定结果进行统计分析。

2.1 星相机测量误差统计

表1列出了随机抽取的2012年至2016年14个时间段星相机A和相机B进行单星相机姿态差分法的标准差统计结果。图3是对应的总误差曲线。

表1 单星相机姿态差分法标准差统计结果

从图3中可以看到，星相机测量误差是无规律的波动过程。由表1计算得到星相机的实际在轨测量误差在4.85″～9.00″范围，均高于实验室标称值5.00″。这说明星相机在轨运行时还受到了标称值误差以外的其他误差因素影响，致使卫星定位精度下降。

图3 星相机A和B的总误差曲线

2.2 基于地面标定场的星地相机夹角误差统计

同时，对天绘一号02星2012年5月20日至2016年12月14日的11次星地相机夹角误差地面标定结果进行了统计，表2为统计结果。图4为绘制的曲线。

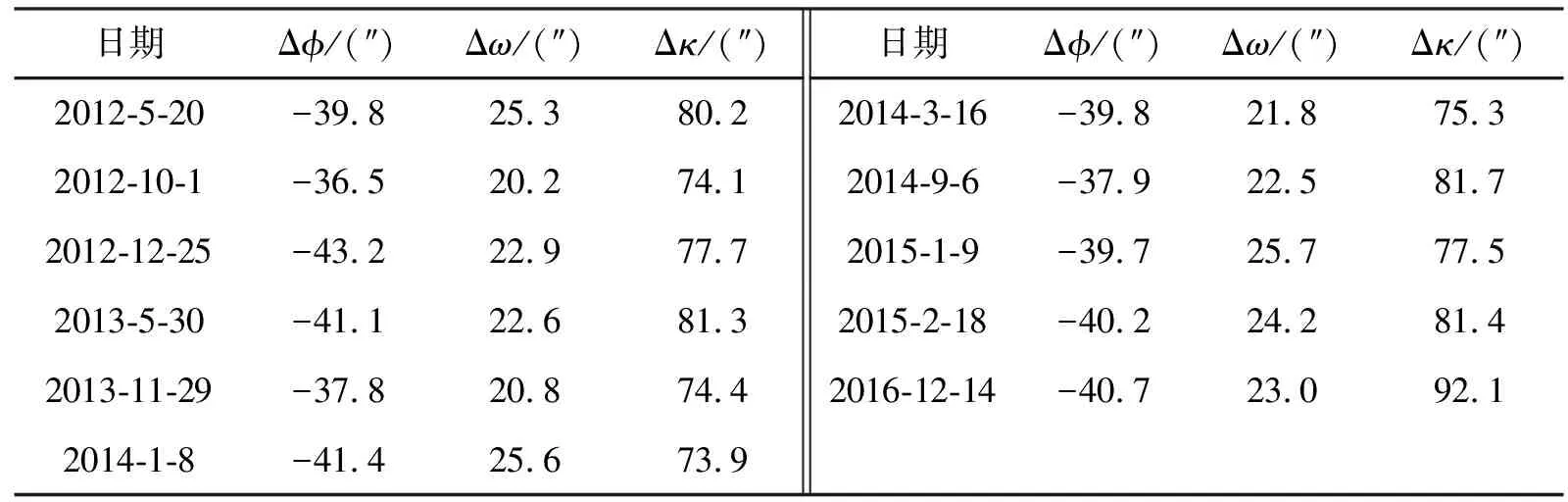
表2 星地相机夹角误差地面标定结果

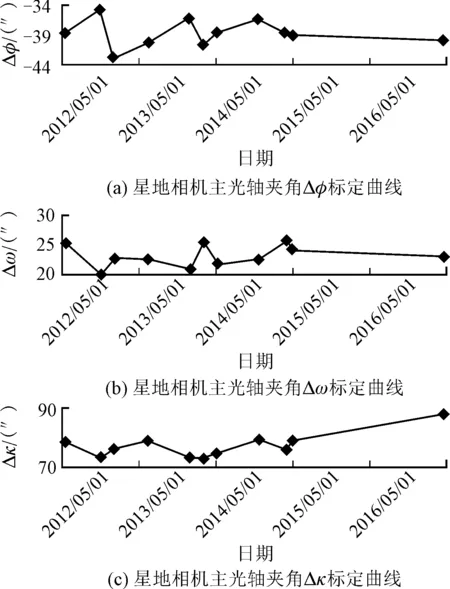
图4 基于地面定标场的星地相机主光轴夹角标定曲线

由图4可以看到，星地相机主光轴夹角变化在长期内是一个无序且缓慢漂移的过程。尽管利用地面试验场标定的方法可以解算星地相机主光轴夹角的变化量，但该方法受制于天气、地形等条件，且目前几个月一次的标定周期难以准确地反映短周期内的变化情况，限制了定位精度的提升。

2.3 误差分析

结合以上分析，参考欧洲太空总署(ESA)制定的星相机通用性能标准ECSS-E-ST-60-20C[8]，依据误差的频率特性可将星相机误差分为瞬时误差、高频误差、低频误差以及偏置误差[9-11]。高频误差可分为像素空间误差和平台高频颤震，低频误差可分为视场空间误差和热形变误差。

瞬时误差、偏置误差、像素空间误差、视场空间误差均在星相机标称模型中考虑，提高标称模型的精度[12]或采用更高精度的标定设备，如多光谱型恒星模拟器，可以对其进行有效的抑制和补偿。平台高频颤震可以通过文献[13-14]在一定程度上被抑制和抵消。随着未来减震隔离措施的改进，该误差的影响将逐步减小。但根据现有的水平，热形变误差还难以完全消除。因此笔者重点讨论分析热形变误差及标定方法。

卫星在轨运行期间，受轨道热环境、安装面边界条件、整机温度梯度和焦面材料退化等因素影响会产生星相机、地相机及其安装结构的热弹性形变误差。虽然目前航天相机的温度控制基本可以达到(20±2)℃，但经过长期的研究发现，相机镜筒及内部光学元件仍会产生非对称热形变[15]，引起镜面倾斜和镜面非轴对称，造成相机主光轴变化，星地相机主光轴之间的夹角也随之变化，且对于不同的相机设计，该变化还难以找到规律。

当前，热弹性形变误差抑制方法主要为星上设计控制，选用低膨胀复合材料，采用一体化和等温化的思想进行光机结构优化设计[2]，提高星相机及安装支架的热稳定性。但从加工制造角度来看，由于当前工艺、技术水平等限制，很难达到理想的温度水平和温度控制水平，热弹性形变误差难以抑制消除。

3 光学测绘卫星相机夹角星上实时定标

笔者提出一种将光学自准直原理应用到航天相机夹角星上监测的实时定标方法，可实现对星地相机夹角的实时定标。其基本思路是：在航天相机载荷系统内部加装准直光源、光斑成像面阵和光路传导装置等器件，通过光斑影像的变化求解出单个相机主光轴的变化，进而解求出相机间夹角的变化，实现高效、快速的星上自主标定。

3.1 单相机主光轴变化监测原理

光学自准直是一种常用的挠曲角测量方法，它的基本原理为当反射镜的法线与光轴成一定的倾角θ时，光线经过反射镜后的偏转为反射镜倾角的2倍，此时该光线的成像点与光线发射点的偏移量s为[16]

s=ftan(2θ) ,

(4)

其中，f为主距。通过测量出偏移量s，即可得到倾角θ。

笔者在前期工作中推导了单个相机星上监测的表达式[17]。图5为单相机主光轴变化监测原理示意图。激光发射装置发射出光源，经过平行光管(或导光棱镜)的传导到达反射棱镜的反射面上，光线反射进入相机镜头，再由镜头光学系统的反射与传导最终成像在光斑记录装置上。若主光轴发生改变，则光斑影像位置发生改变，通过计算额定影像位置与实际影像位置之间的距离便可以解算出相机主光轴的变化量。

主光轴发生的偏转可以分解为：在自身像空间坐标系下，主光轴绕X轴的旋转量Δβ、绕Y轴的旋转量Δα以及绕视轴的旋转量Δγ。同时该方法还可以反映出主距变化量Δf。以主光轴绕X轴旋转为例，光斑影像位置的变化如图6所示。

图5 单相机主光轴变化监测原理示意图

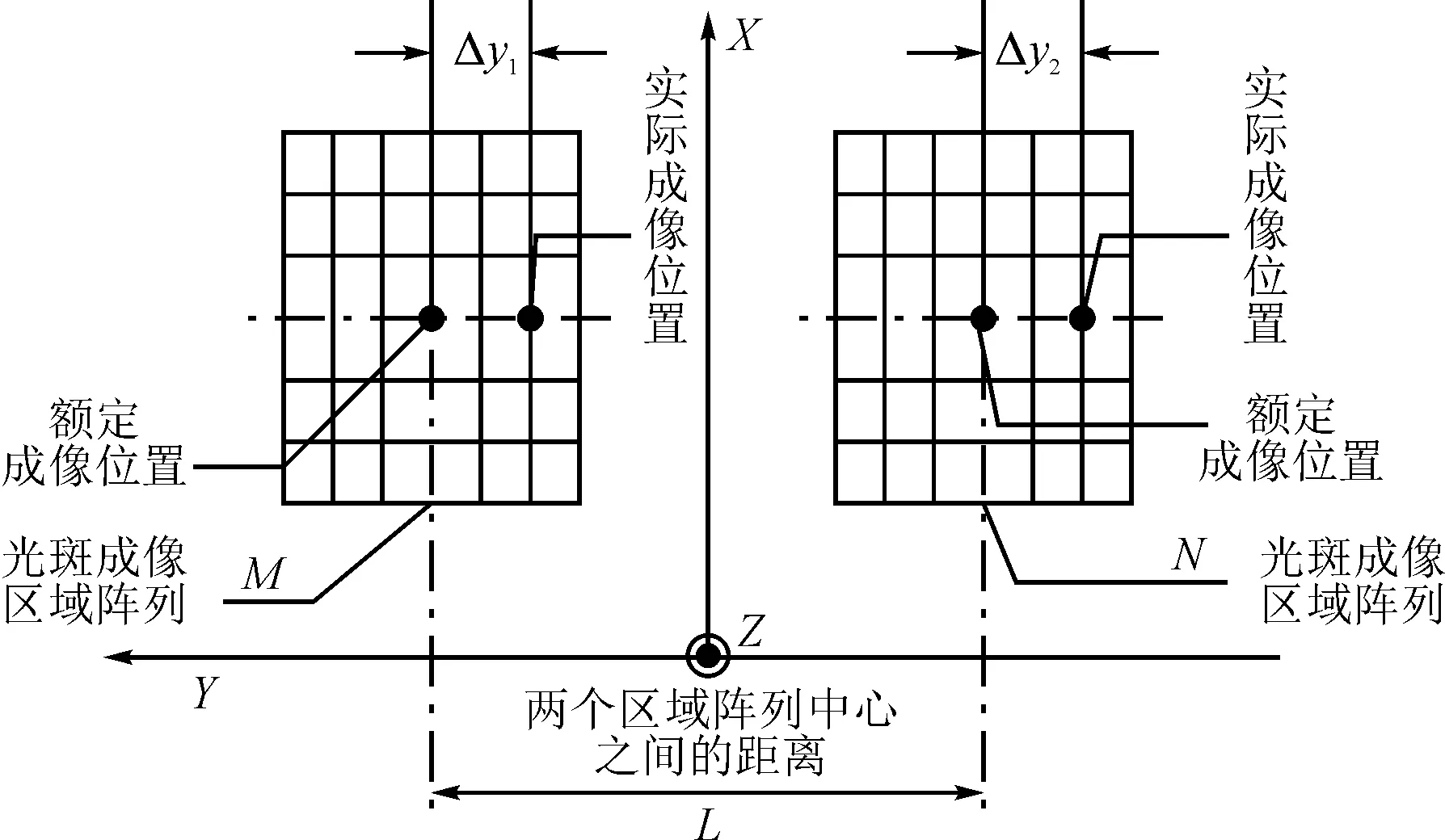
图6 光斑影像位置变化示意图

经过推导可知,在三个旋转量中，Δβ和Δf会引起光斑影像位置的Y坐标改变，Δα和Δγ会引起光斑影像位置的X坐标改变。由此可以得到单个相机主光轴综合在轨变化的表达式:

(5)

其中，δ为像素大小，f为主距，YM与YN为光斑影像位置左右区域阵列的Y轴变化量，XM与XN为光斑影像位置左右区域阵列的X轴变化量。

3.2 相机间主光轴夹角定标方案

基于节3.1所述的方法，分别对星相机和地相机主光轴进行在轨监测，标定出各相机主光轴的变化量。结合节1.2星地相机转换关系，可求出星地相机之间夹角的变化量。数据处理流程如图7所示。

图7 星地相机夹角数据处理流程

由式(1)和式(2)可得星地相机夹角变化后的矩阵：

(6)

其中，(Δαt, Δβt, Δt)为地相机主光轴绕三轴的旋转量，(Δαs, Δβs, Δγs)为星相机主光轴绕三轴的旋转量，均可由式(5)求出；为式(1)已知；MΔt、MΔs的表达式如下：

(7)

(8)

3.3 相机间主光轴夹角误差推导

根据式(5)及误差理论，可以得到Δβ、Δα、Δγ的测量误差σβ、σα、σγ表达式：

(9)

其中，σk为光斑影像位置确定的总角误差;σβ、σα、σγ表示Δβ、Δα、Δγ的测量误差。

由式(6)和式(9)推导得到：

(10)

其中，σφ、σω、σκ为Δφ、Δω、Δκ的测量误差。

进一步，得到星地相机主光轴夹角测量误差矩阵

(11)

由此便可以求出星地相机主光轴夹角测量误差σφ、σω、σκ分别为

(12)

3.4 相机间主光轴夹角精度分析

基于前期的工作[17]基础，从实验室条件和在轨失重条件两个方面对相机间主光轴夹角进行精度分析。

记录装置误差会造成光斑影像位置确定的总角误差 ，其与记录装置受温度和结构的变化有关。在实验室条件下，计算得到k约为0.430″。将其代入式(9),得到各参数计算结果如表3所示。

偏航角的定标精度相较于滚动角、俯仰角而言较差，但偏航角的误差可通过后续摄影测量处理较好地消除，因此不是关注重点。将表3中的计算结果代入式(12)，得到在实验室条件下星地相机夹角变化量的精度如表4所示。

表3 实验室条件下各参数计算结果

表4 实验室条件下星地相机夹角变化量精度

在轨失重状态下，设备在重力作用下出现的光学元件弯曲可忽略不计，进而可得到地相机定标光斑记录装置影像位置和星相机定标光斑记录装置影像位置的确定误差k约为0.145″[18]，将其代入式(9),得到各参数计算结果如表5所示。将表5中的计算结果代入式(12)，得到在在轨失重条件下星地相机夹角变化量的精度如表6所示。

表5 在轨失重条件下各参数计算结果

表6 在轨失重条件下星地相机夹角变化量精度

根据表4和表6，可以看到实验室条件下俯仰和横滚方向星地相机夹角变化量的精度约0.33″(1Hz)；在轨条件下俯仰和横滚方向星地相机夹角变化量的精度约为0.13″(1Hz)。

4 总 结

笔者结合天绘一号长期实测数据统计分析了相机及相机夹角的主要误差源，并得出由热弹性形变误差造成的星地相机主光轴夹角变化是影响卫星定位精度进一步提升的重要因素，对此提出了一种基于光学自准直原理的相机夹角星上定标方法。该方法不依赖地面定标场，不改变相机原有光路，可实现对相机夹角的星上实时自主定标，较目前常用的定标手段(精度5″左右，频率2～4次/年)，在时效性和精度上都有大幅提升。未来笔者将会基于更多的实验数据在全链路误差分析、工程可行性分析两方面进行深入的研究。