一种新的低空目标角度估计方法

黄保涛，蒋 敏，伍光新，邢文革

(南京电子技术研究所，江苏 南京 210039)

在低仰角目标探测、跟踪过程中，雷达信号在低空复杂环境中往往会受到由地、海面反射产生的多径回波的影响，此时的多径回波信号和直达信号是高度相关的，从时域、频域上都很难对两者进行分辨[1-3]。低空环境下的多径效应造成回波信号幅度的随机衰落，这种幅度畸变会使低空目标角度估计结果产生严重偏差。

当前解决低空目标俯仰角测量问题的方法主要有两类，即基于阵列信号处理的高分辨测角算法和最大似然估计算法[4]。在高分辨测角方面，近年来去除多径回波信号相关性的测角算法得到充分发展，这类算法是通过空间平滑或矩阵重构来解决相关信号造成的协方差矩阵秩亏缺问题的[5]。基于空间平滑处理的多重信号分类算法(Spatial Smoothing MUltiple SIgnal Classification, SS-MUSIC)、改进的多重信号分类算法(Improve MUltiple SIgnal Classification, IMUSIC)[6-8]是常用的相关信号角度估计算法。这类算法的估计性能易受信噪比和快拍数的影响，而在低空环境中很难获得连续的高信噪比快拍数据。文献[4]提出一种子阵级角度估计方法，但基于目标直达角度和反射角度相同的假设限制了该方法的进一步推广。文献[5]提出一种新的低空角度测量方法，通过建立微扰多径模型，划分角度空间网格构建冗余字典，再利用正交匹配追踪求解稀疏信号矩阵，以获得目标的真实角度。最大似然估计算法也可以完成低空环境下目标的角度估计，但估计性能依赖于对低空信号传播过程的精确建模，且运算量过大，无法满足实时测角的要求[9-10]。

针对多径畸变对波达角度(Direction Of Arrival, DOA)估计产生影响的问题，提出一种不借助特征分解(Without Eigen Value Decomposition, WEVD)的波达角估计算法，实现多径情形下单目标角度信息估计。该算法以三子阵天线为基础，在直达-反射两个维度上进行角度谱搜索，完成在目标反射角度和直达角度的估计。不同于传统相关信号测角算法中利用空间平滑方法实现信号去相关的思想，该算法只需借助空间平滑构建三子阵天线，对去相关性能没有要求。另外，该算法不需要对矩阵进行特征分解，也无需预先估计相关信号的信源数，避免了信源估计误差对角度测量的影响。

1 信号模型

假设阵列结构为均匀线阵，阵元数量为M、阵元间距为d。存在波长为λ、角度为θ的窄带信号入射时阵列的方向矢量：

(1)

若同时存在K路窄带入射信号，入射角度分别为θ1,θ2,…,θK，则阵列的M×K阶方向矩阵A(θ)满足

A(θ)=[a(θ1),a(θ2),…,a(θK)] 。

(2)

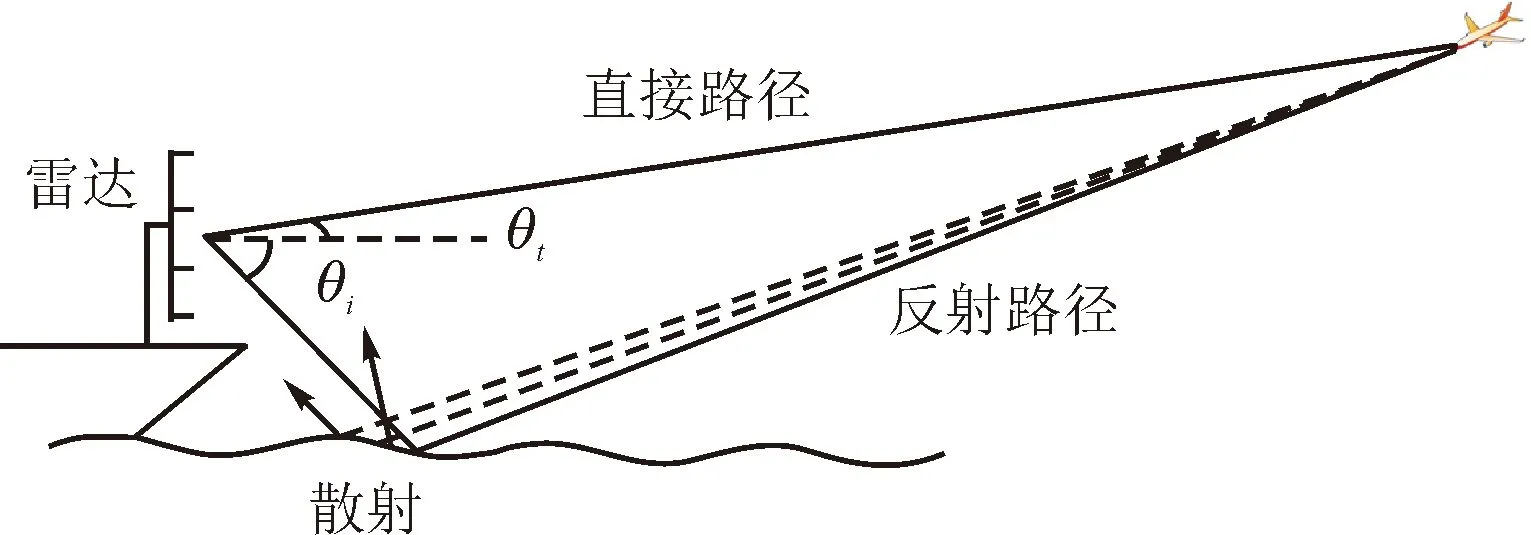
图1 海面目标多径模型

为方便阐述该算法，建立如图1所示的海面低空目标多径回波模型。回波信号中包括直接反射、镜面反射和散射3个部分。雷达回波能量主要集中在镜面反射回波和直达回波中，散射回波对角度估计影响有限，模型主要研究镜面反射干扰下的角度估计算法。

考虑雷达的发射信号为s(t)，ρ为镜面反射衰减因子，τi表示第i条路径的传输时延。根据图1所示的多径模型，阵列接收的回波信号由直达-直达、直达-反射、反射-直达、反射-反射4个部分组成，因此阵列接收信号可以简化成S(t)=[s(t-τ1),ρs(t-τ2),ρs(t-τ3),ρ2s(t-τ4)]T。此时阵列的接收信号可以表示为

X(t)=AS(t)+N(t) 。

(3)

在多径模型下，考虑回波信号的4个部分。式(3)中的方向矩阵满足A=[a(θt),a(θt),a(θi),a(θi)]，其中θt是直达回波的入射角度，θi是反射回波的入射角度。N(t)=[n1(t),n2(t), ...,nM(t)]T，为天线单元的加性噪声，服从方差为σ2的高斯独立分布。

2 低仰角估计方法

2.1 三天线阵列测角

考虑不同阵元之间的噪声信号相互独立，阵列接收信号的协方差矩阵R可以表示成

R=E[X(t)X(t)H]=AS(t)S(t)HAH+N(t)N(t)H。

(4)

信号自相关矩阵满足Rs=S(t)S(t)H, 噪声服从方差为σ2的高斯独立分布，即满足N(t)N(t)H=σ2I。进一步可以将阵列接收信号的协方差矩阵写成

R=ARsAH+σ2I。

(5)

根据式(5)可知，目标的角度信息包含在信号空间ARsAH中。在已知信号的协方差矩阵的情况下，需要寻找满足当估计角度和入射角度相等时与信号空间正交的矢量，以完成目标角度的估计。假设符合条件的正交矢量为V，则V满足

VHARsAHV=0 。

(6)

通过信号模型中的分析可得阵列方向矩阵A的具体形式。为了方便描述，令

(7)

(8)

则A可表示为式(8)的形式。令AHV= 0，当阵元数量M= 3时，可以得到符合要求的正交矢量，即

(9)

对构造的正交矢量式(9)分析可知，正交矢量V(θt,θi)与目标的直达角度、反射角度两个参数有关。获得3个天线阵列接收信号的正交矢量后，利用接收信号的协方差矩阵R对两个未知参数(目标直达角度θ1, 目标反射角度θ2)进行角度谱估计。角度谱估计的表达式为

(10)

根据构造V的约束条件(6)可知，仅当θ1=θt,θ2=θi时，角度谱P(θ1,θ2)才会在角度搜索空间中形成谱峰。角度搜索过程中对目标回波信号的直达角度维度和反射角度维度进行二维搜索处理，当两个维度分别搜索到回波信号直达角度和反射角度处时，由于V(θt,θi)与AH满足正交关系，此时谱估计表达式满足

(11)

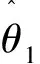
2.2 多天线阵列测角

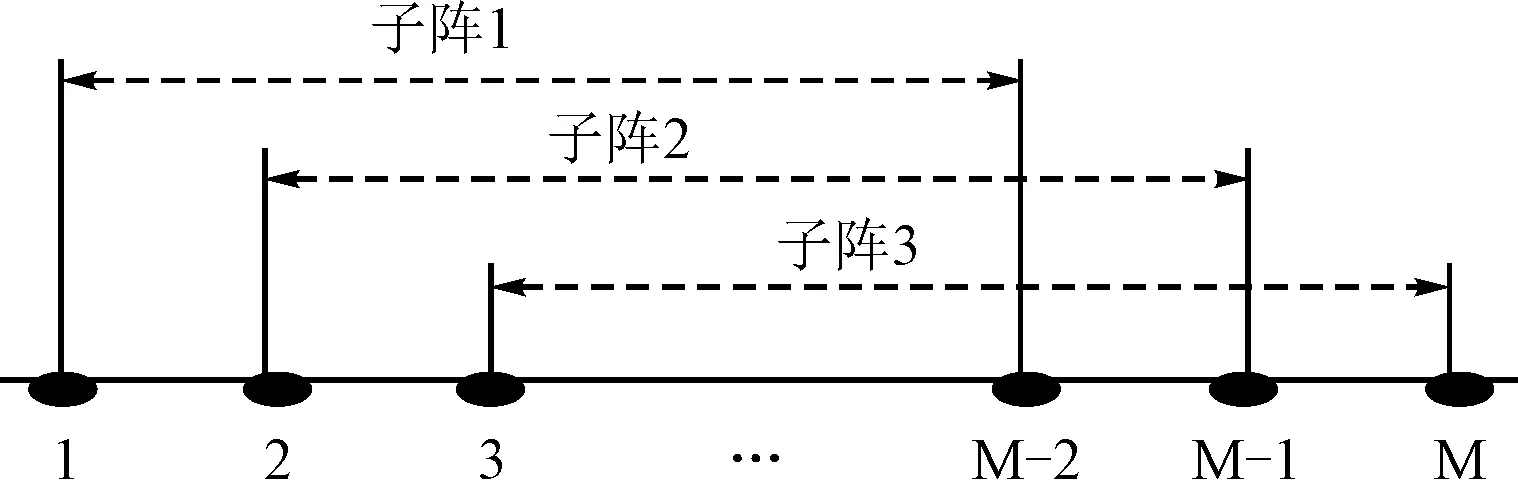
图2 多天线子阵划分处理

当接收单元的数量M> 3时，上述3个天线测角方法无法使用。此时考虑进行空间平滑处理，将多天线阵列划分成3个天线子阵。对于多接收单元的空间平滑处理如图2所示。

空间平滑后总共获得3个子阵。第l个子阵的输出可以表示为

Xl(t)=AM-2Dl-1S(t)+N(t)，l=1,2,3。

(12)

AM-2是维度为(M- 2)×K的方向矩阵，其列矢量为

(13)

式中,k= 1, 2,…,K，是M- 2维的方向矢量。

矩阵D满足

(14)

N(t)= [n1(t),n2(t), ...,nM-2(t)]T，为噪声矩阵，所以空间平滑后第l个子阵的协方差矩阵为

Rl=AM-2Dl-1Rs(Dl-1)H(AM-2)H+σ2I。

(15)

因此，得到空间平滑协方差矩阵:

(16)

经过空间平滑处理之后，将M(M> 3)天线阵列，划分成3个子阵天线阵列。将由式(16)中获得的协方差矩阵R代入到式(10)中，再通过角度谱搜索即可获得多天线单元接收时低空目标的角度信息。

进一步将模型推广到平面阵中。假设平面阵列阵元数为N×M，N为水平方向阵元数，M为垂直方向阵元数。考虑目标入射平面阵时波达方向为(θ, Ф)，其中θ、Ф分别代表目标的俯仰角和方位角。若多径回波的方位角相同，而俯仰角有θt和θi两种情况，则水平方向上N个阵元的方向矩阵为

(17)

垂直方向上M个阵元的方向矩阵为

(18)

对于二维波达角估计，在考虑多径回波影响的情况下，直接采用不借助特征分解算法进行目标角度估计时，需要在方位角度、俯仰直达角、俯仰反射角3个维度上进行角度搜索，计算复杂度显著变大。由于多径回波的方位角度相同，利用维度降低方法[11]，先在方位维度上估计目标的方位角，再利用不借助特征分解算法对垂直方向上的方向矩阵处理，可获得多径情况下目标在俯仰方位上的真实角度。

3 示例仿真

为验证上述算法的性能，实验仿真过程中分别对低空静态目标和运动目标的角度进行估计，结合SS-MUSIC测角算法[7]和WEVD算法进行对比分析。在静态目标角度估计仿真中，研究不借助特征分解算法在不同多径数下的性能。实验中，雷达工作频率fc= 10 GHz，脉冲宽度Tp= 10 μs，脉冲重复间隔Tr= 100 μs，采用线性调频信号，信号带宽B= 5 MHz，天线单元数量M= 10，单元距离d=λ/2。仿真中对静态目标回波信号进行脉压处理，运动目标回波信号进行相参积累处理，最后利用处理过的回波信号对目标的角度信息进行估计。

3.1 静止目标角度估计

当雷达高度hr= 15 m时，按照表1的多组目标参数对静态目标进行仿真分析，获得对目标角度估计的结果。

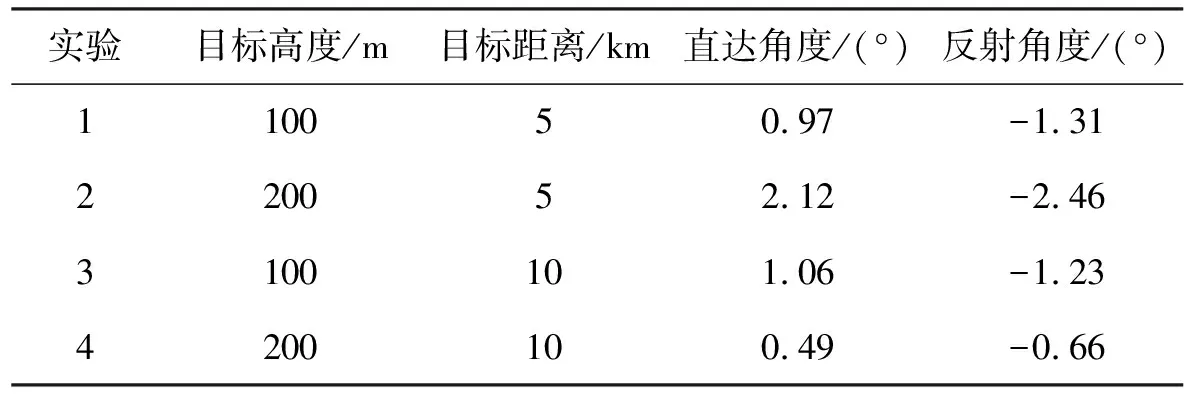
表1 仿真参数设置

对上述4种情形在信噪比为0 dB时分别使用WEVD方法和SS-MUSIC方法进行100次蒙特卡罗仿真，获得目标角度在直达-反射两个维度上的分布散点图。图3中给出仿真结果的分布情况。对估计结果进行统计分析，获得4次实验的误差分析数据，如表2所示。

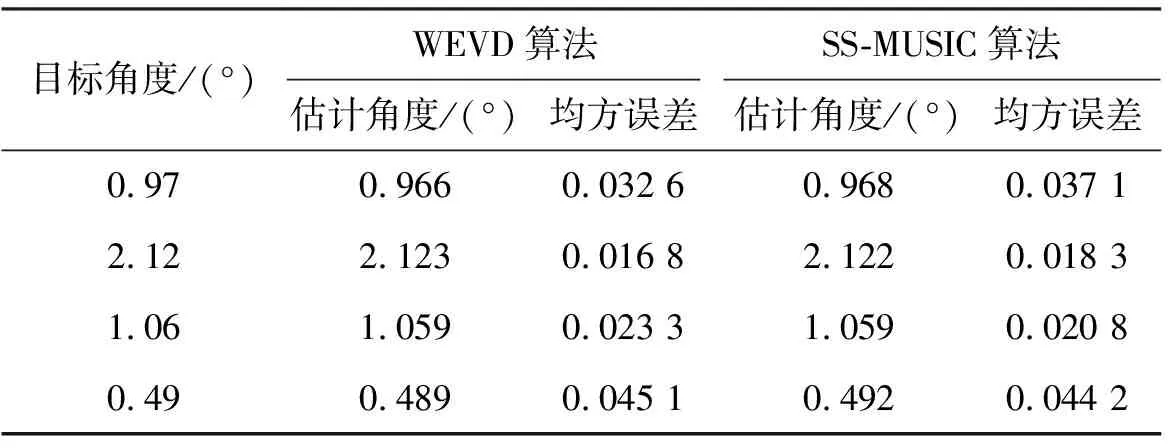
表2 静态目标仿真结果对比

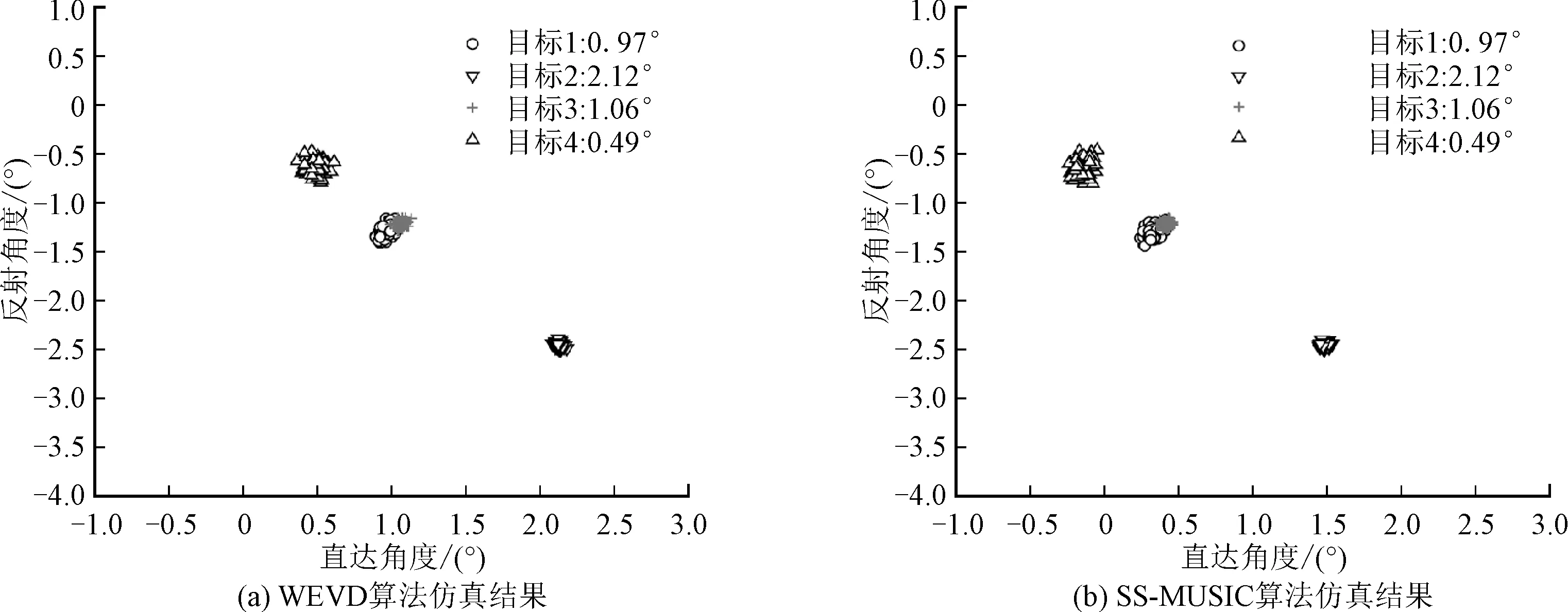
图3 静态目标100次蒙特卡罗仿真结果

根据仿真结果，SS-MUSIC算法和WEVD算法的估计均值和真实角度基本一致。可见对于静态目标，WEVD算法性能不逊于SS-MUSIC算法。但是，使用SS-MUSIC算法时，需要从多个估计值中分选出目标的直达角度，而WEVD算法在直达、反射两个维度上进行二维搜索避免了对估计角度的分选过程。在均方根误差方面，目标直达角度和反射角度越接近，均方根误差越大，说明目标角度越小，多径效应对目标角度估计的影响越大。

3.2 多径数对角度估计影响

当雷达高度hr= 15 m时，对高度ht= 100 m、距离R0= 5 km的静态目标进行目标角度估计受多径数量影响的分析。仿真中多径回波分别设置为以下5种情况：2路径，角度为{0.97°, -1.31°}；3路径，角度为{0.97°, -1.31°, -0.7°}；4路径，角度为{0.97°, -1.31°, -0.7°, -0.6°}；5路径，角度为{0.97°, -1.31°, -0.7°, -0.6°, -0.3°}；6路径，角度为0.97°, -1.31°, -0.7°, -0.6°,-0.3°, -0.9°}。当信噪比为0 dB时，进行100次蒙特卡罗仿真，分析角度估计的均方误差。

从图4中可以看出，随着多径数的增加，均方误差呈上升趋势。实验结果表明,随着环境的复杂化,角度估计性能逐渐下降。这符合仰角测量的实际情况，但当多径数增加到一定值之后,上升趋势明显减缓。

3.3 水平运动目标跟踪

当雷达高度hr= 15 m时，对高度ht= 100 m、起始距离R0= 5 km，径向速度v= 50 m/s的运动目标进行角度估计。仿真设置雷达的数据率为1 s，共对目标进行1 min的跟踪。

图5展示了水平运动目标在信噪比为-10 dB时，SS-MUSIC算法和WEVD算法对动目标角度跟踪的性能。图中虚线表示目标在不同位置处根据几何关系确定的反射角度。从仿真结果可以看出，SS-MUSIC算法在目标角度较小的情况下，由于空间平滑算法难以对回波信号进行有效的去相关，因此会产生严重抖动；而WEVD算法只利用空间平滑实现降维，不依赖于去相关效果，所以对角度抖动有明显的抑制效果。

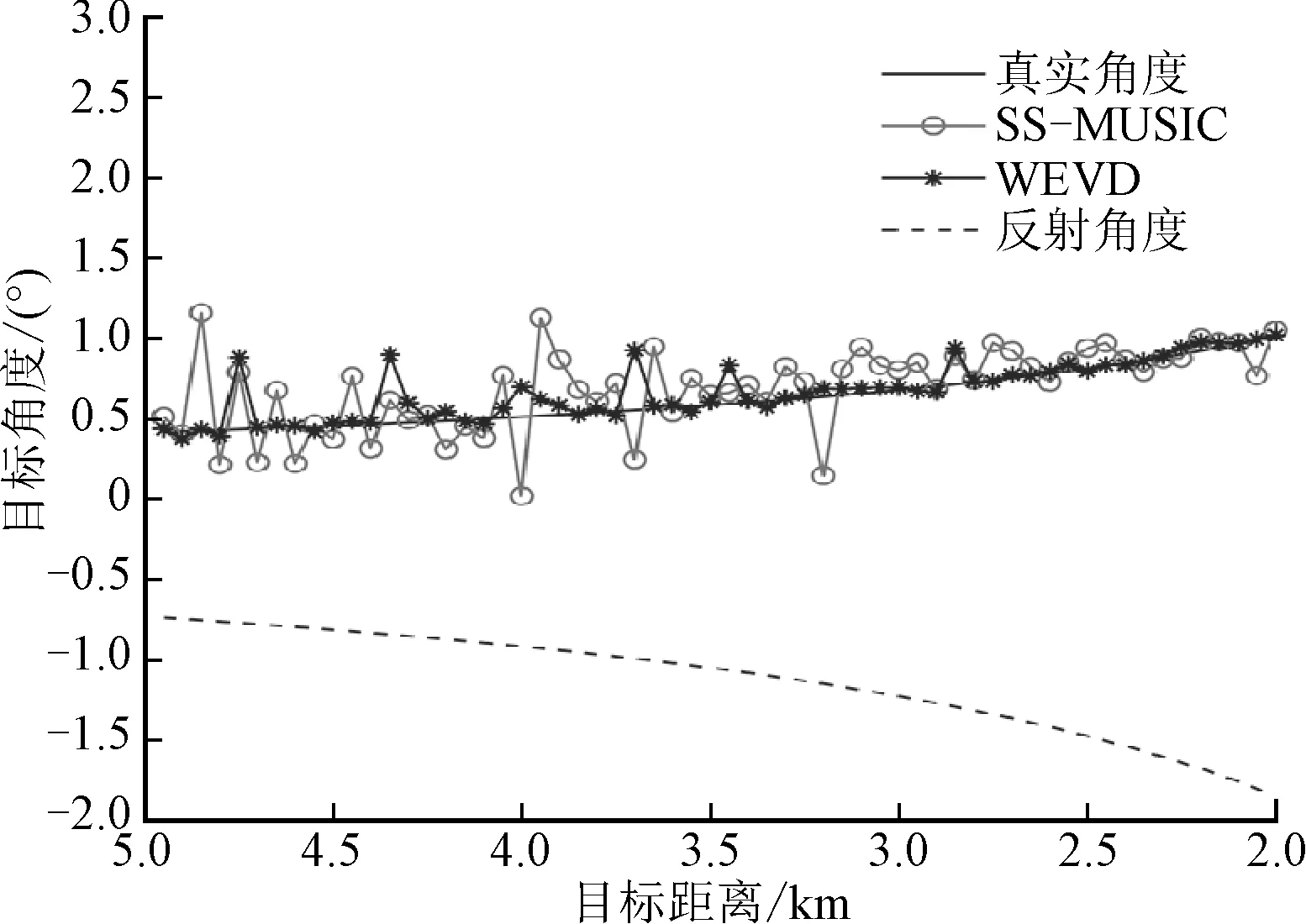
图5 信噪比为-10 dB时径向运动目标角度跟踪

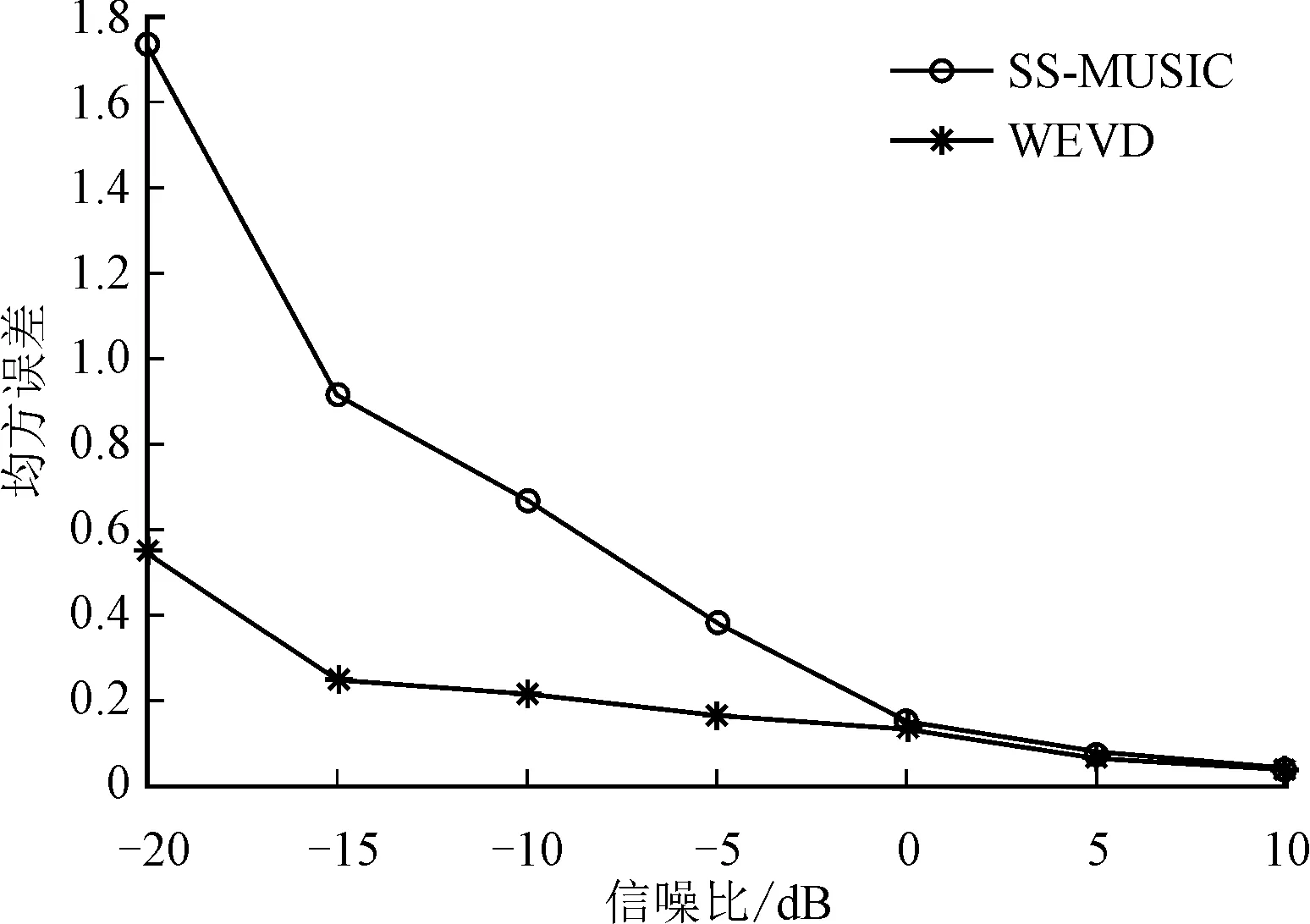
图6 径向目标角度跟踪的均方根误差

在水平运动目标角度跟踪过程中，均方根误差随信噪比的变化趋势如图6所示。显然在低信噪比时，WEVD算法效果明显优于SS-MUSIC算法的。信噪较低时，通过特征分解难以区分信号子空间和噪声子空间，导致SS-MUSIC算法失效；WEVD算法避免了特征分解划分子空间的过程，有效地提升了低信噪比环境下的角度跟踪性能。

3.4 垂直运动目标跟踪

当雷达高度hr= 15 m时，对起始高度ht= 50 m、距离R0= 5 km，上升速度v= 10 m/s的运动目标进行角度估计。仿真设置雷达的数据率为0.1 s，对目标进行15 s的角度跟踪。

分别对信噪比为 -10 dB、0 dB的对垂直运动目标进行角度跟踪。图7显示信噪比为-10 dB时，WEVD方法对垂直目标跟踪的角度效果明显好于SS-MUSIC算法的。图8中当信号的信噪比增加到0 dB时，WEVD算法在小角度时跟踪效果优于SS-MUSIC算法的。该结果与水平运动目标跟踪中对SS-MUSIC算法和WEVD算法的误差分析结果一致，说明WEVD算法在低信噪比和小角度时角度估计效果具有稳定性。

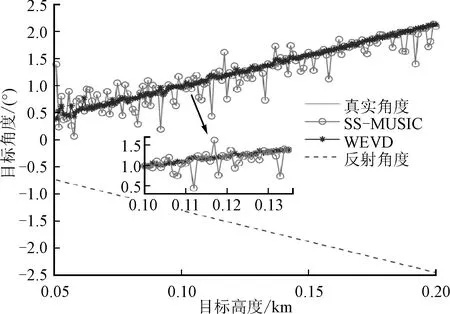
图7 信噪比为-10 dB，垂直运动目标角度跟踪

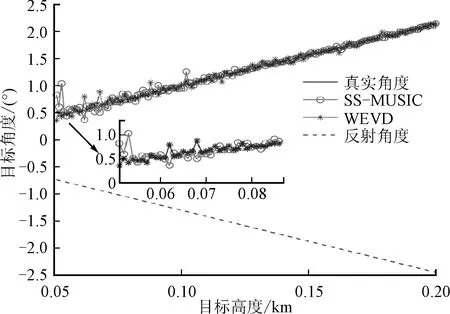
图8 信噪比为0 dB，垂直运动目标角度跟踪

4 结束语

在低空多径模型中，笔者提出不借助特征分解算法，通过构造三天线接收信号的正交矢量，完成对目标真实角度和反射角度的同时估计。该方法避免了传统方法中的特征分解、信源数量估计，减少了信噪比和信源估计对目标角度估计的影响；并且不依赖空间平滑对相关信号的去相关效果，提升了小角度目标估计的性能。通过仿真验证对于低信噪比和小角度条件下的运动目标，表明笔者提出的新型估计算法的性能比传统SS-MUSIC算法的显著优越。