WiFi指纹定位中改进的加权k近邻算法

王博远，刘学林，蔚保国，贾瑞才，甘兴利，黄 璐

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001；2.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；3.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081)

由于室内环境中卫星导航信号的可用性无法得到保证，全球导航卫星系统在室内定位领域的应用受到限制[1]，因此建立一套准确可靠的室内定位系统以满足室内位置服务的需求非常重要。随着智能手机的快速发展，WiFi信号接收模块已内置于智能手机中，同时在一些公共场所，如办公楼、车站、商场等，无线局域网也已经实现了广泛的覆盖，WiFi信号指纹定位已成为目前最流行的室内定位方案之一。WiFi指纹定位可大体分为离线阶段和在线阶段。在离线阶段，工作人员在实际场地采集WiFi指纹，包括每个参考点的位置坐标及每个参考点处的接收信号强度值。每一对接收信号强度值和位置坐标确定了一个独一无二的参考点，并按照一定的数据格式存入指纹数据库中[2]。在在线阶段，用户在接收端获得当前位置的信号强度，通过搜索指纹库找到与信号强度读数最匹配的几个参考点，将匹配到的参考点坐标进行平均或者加权平均，估计出用户当前的位置坐标。

现存的WiFi指纹定位方法大都采用确定性方法，包括最近邻算法，k近邻算法和加权k近邻算法。微软公司设计的RADAR系统[3]是较早使用WiFi指纹定位的室内定位系统，其利用k近邻算法使得系统可以满足房间级别的定位精度。为了提高WiFi指纹定位系统的定位精度和系统稳定性，研究人员提出了许多WiFi指纹定位算法。文献[4]针对定位系统因多路径效应等因素所导致定位精度降低的问题，提出了一种基于到达时差的混合定位算法。文献[5]根据位置距离使用相似性传播聚类对最近邻参考点进行聚类。通过比较聚类中心和在线接收信号强度读数之间的信号距离以及参考点的数目，保留可能性最大的参考点类别，然后使用加权k近邻算法估计用户位置。文献[6]通过对室内环境的分析，利用信号传播损耗模型建立了似然函数模型，运用马尔可夫蒙特卡罗算法对似然函数中的位置坐标进行了估计，具有快速收敛和高精度的优势。文献[7]采用k均值算法把在每个参考点处来自每个无线接入点的一组信号作为一个类进行计算，将不属于该类的数据剔除掉，从而提高了WiFi指纹数据库的质量。文献[8]指出在WiFi指纹定位中小的接收信号强度值具有和大的接收信号强度值同等的意义，以用来表示与无线接入点距离的不同，因此不应该简单地将数值小的接收信号强度舍掉。文献[9]设计了3种不同加权距离的k近邻算法，发现基于曼哈顿距离的k近邻算法性能最好。文献[10]通过实验证明，传统的加权k近邻算法将参考点接收信号强度与测试点接收信号强度差值的倒数作为参考点的权值进行加权平均，这并不符合WiFi信号具有不均匀空间分辨率的特性，因而降低了定位精度。根据上述提到的方法可知，现存的基于最近邻机制的定位方法大都利用不同点间的信号距离来判断相互之间的物理距离，并将其作为指纹匹配和位置估计的依据。然而，由于室内环境会受到反射、折射以及多径效应的影响，WiFi信号具有很强的波动性，这将给信号距离的计算带来误差。同时根据WiFi信号的损耗模型可知，接收信号强度的变化值与传播距离呈对数关系，即两者的关系是非线性的[11]。因此，为了解决WiFi指纹定位系统中由于WiFi信号的波动性和衰减特性导致传统的信号距离不能很好地反映物理距离的问题，笔者提出了一种改进的加权k近邻算法。将WiFi信号的波动性以及接收信号强度与物理距离的非线性关系引入到信号距离的计算中，给不同的信号强度差值分配不同的加权系数，使用信号的加权欧氏距离作为加权k近邻算法的距离度量，提高传统的加权k近邻算法的定位精度。

1 指纹数据库构建

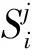
(1)

(2)

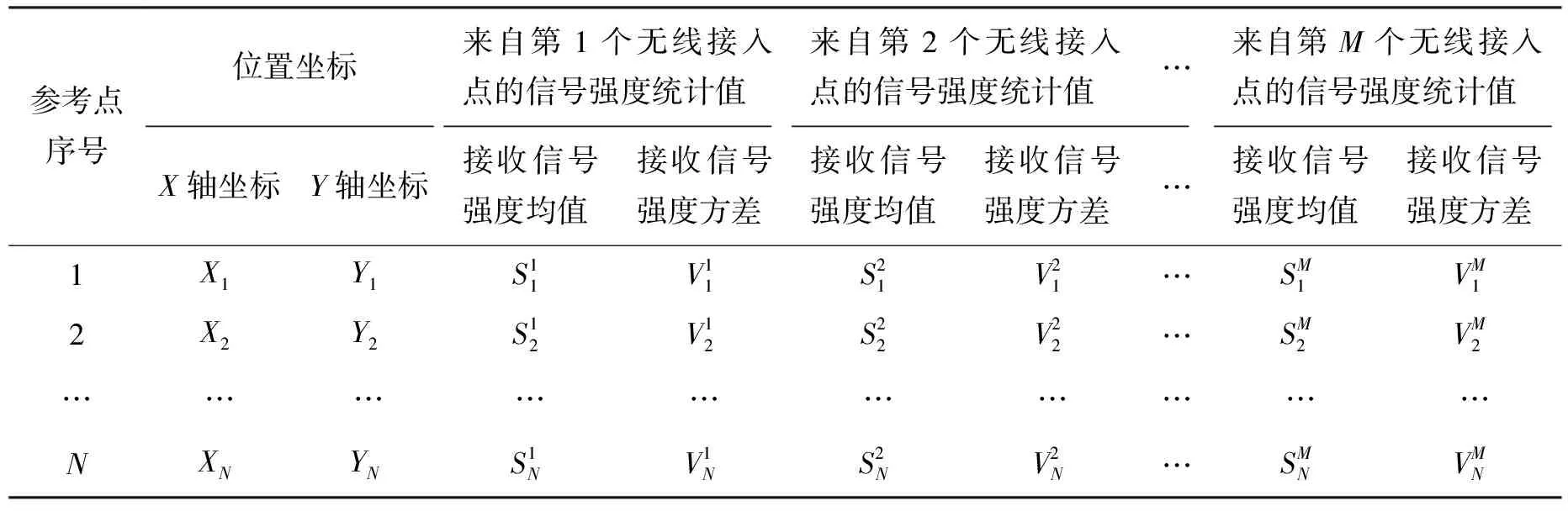
表1 指纹库数据格式

2 改进的WiFi指纹定位算法

根据室内WiFi信号的波动性、接收信号强度与物理距离的非线性关系，使用信号加权欧氏距离作为加权k近邻定位算法的距离度量，提出了一种改进的加权k近邻算法。现存的加权k近邻算法大多利用参考点和测试点之间的信号欧氏距离来判定其间的物理距离di,可表示为

(3)

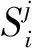
(4)

(5)

经典信号对数损耗模型[12]可表示为

PL(d)=PL(d0)-10ηlg(d/d0)+χσ,

(6)

其中，PL(d)表示距离无线接入点为d处的信号强度值；d0为参考距离，一般设为1 m；PL(d0)为参考距离处的信号强度值；η为路径损耗指数；χσ代表标准差为σ的高斯随机变量。

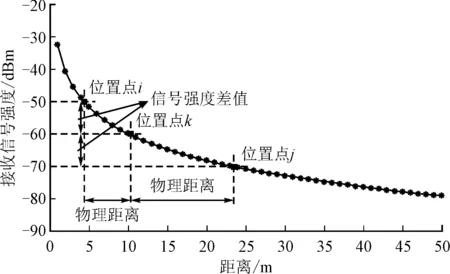
图1 接收信号强度与物理距离的关系示意图

理想WiFi信号环境下的信号损耗曲线如图1所示，其中d0=1 m，PL(d0)=-31.7 dBm，路径损耗指数η=2.76[13]。如式(3)所示，现存的信号欧氏距离只考虑了信号强度差值。然而从图1可以看出，信号强度差值与物理距离关系是非线性的，随着离无线接入点的距离的增加，信号衰减速度变慢，相同大小的信号强度差值也可以代表不同的物理距离。因此要想使信号距离更准确地反映物理距离，不仅要考虑信号强度的差值，还要考虑每一对位置点信号强度值的总体大小。因此，文中设计了一种加权欧氏距离，通过给不同的信号强度差值分配不同的权值来平衡信号距离和物理距离之间的差异，计算如下：

(7)

(8)

(9)

根据测试点与所有参考点的信号加权欧氏距离的大小，选出距离最小的k个参考点作为最近邻参考点估计用户的位置：

(10)

(11)

其中，(X,Y)为估计的位置坐标，(Xi,Yi)为第i个参考点位置坐标，ωi为第i个参考点位置坐标的权重。相比于现存的加权k近邻算法，使用加权欧氏距离选出的最近邻参考点以及参考点的坐标权重更加合理，可以大大提高定位精度。

为了确定提出的算法满足实时定位需求，可计算算法的时间复杂度：

(1)计算测试点与N个参考点的信号强度平均值以及来自不同无线接入点的信号强度差值的加权系数，时间复杂度为O(N+NM)，即O(NM)。

(2)计算测试点与N个参考点的加权欧氏距离，时间复杂度为O(N)。

(3)对所有加权欧氏距离排序，时间复杂度为O(NlbN)。

(4)计算k个最近邻参考点的坐标权重以及对最近邻参考点坐标进行加权平均，时间复杂度为O(k)。

传统的加权k近邻算法的时间复杂度为O(NlbN)+O(k)。因此，只有当M>lbN时，所提出算法的时间复杂度O(NM)+O(k)才会大于传统的加权k近邻算法的，但仍可以满足实时定位的需求。在其他情况下，文中所提出的算法的时间复杂度为O(NlbN)+O(k)，与传统算法处于同一个量级。

此外，为了更直观地说明所提出的加权欧氏距离的优势，笔者基于仿真数据对比了改进的加权k近邻算法与传统的加权k近邻算法。考虑一维坐标系中的2个无线接入点、2个参考点和5个测试点，根据式(6)的信号对数损耗模型，可以得到不同距离处的各点接收信号强度值，模型参数设置与图1相同。表2列举了5个测试点与2个参考点间的信号欧氏距离和信号加权欧氏距离，以及每个测试点与2个参考点的两种信号距离的比值。可以看出，相比于传统的信号欧氏距离，测试点与两个参考点的信号加权欧氏距离的比值更接近于相应的物理距离的比值。这说明加权欧氏距离更能反映位置点间的物理距离，因此在寻找最近参考点以及计算不同参考点的坐标权重的过程中，其定位性能优于传统的加权k近邻算法的。

表2 基于仿真数据的测试点与参考点间信号欧氏距离和信号加权欧氏距离

3 实验结果及评估

3.1 实验环境及实验设置

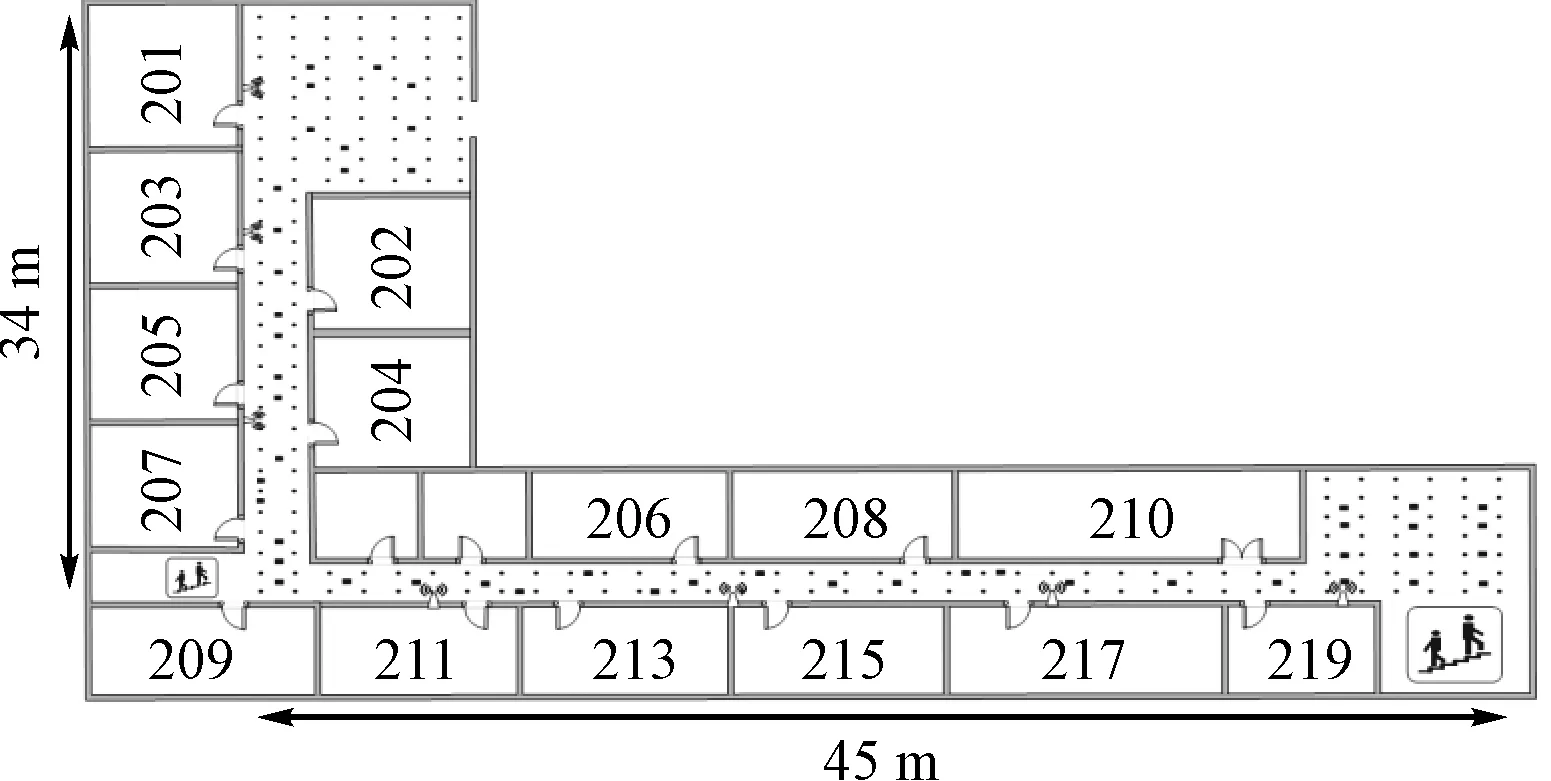
图2 WiFi指纹定位实验环境

为了验证文中提出的定位方法性能，在某实验楼2楼进行WiFi指纹室内定位实验。如图2所示，实验场地内共布置7个无线接入点，200个参考点和50个测试点，相邻参考点的距离为1.2 m。实验设备为小米MIX 2智能手机，WiFi信号采样频率为1 Hz。每个测试点处采集接收信号强度数据的时间为60 s，并取其平均值作为在线接收信号强度量测值。

3.2 实验结果分析

为了验证WiFi信号的衰减特性，笔者采集了所有无线接入点在不同距离处的信号强度值，每个距离处采集时间为60 s，平均后的信号强度值如图3所示。

图3 无线接入点1～3在不同距离处的信号强度值

图4 无线接入点4～7在不同距离处的信号强度值

从图3和图4可以看出，由于在室内环境中WiFi信号受到反射、折射、绕射以及多径效应的影响，实测的接收信号强度值呈现出波动性，但仍然可以很好地逼近WiFi信号损耗模型曲线，即随着距离无线接入点距离的增加，信号衰减速率变慢。这证明了笔者提出的信号加权欧氏距离能够适用于真实的定位场景。

为了更直观地展示改进的加权k近邻算法在搜索最近邻参考点和位置加权估计的优势，随机选择了5个参考点，比较了改进的加权k近邻算法和基于欧氏距离的加权k近邻算法的最近邻参考点选择以及定位误差。表3根据参考点与测试点信号距离由小到大的顺序，列举了前4个最近邻参考点以及相应的归一化物理距离。可以看出，对于基于欧氏距离的加权k近邻算法所选择的最近邻参考点，其与测试点的物理距离排序与信号欧氏距离的排序并不一致。而对于改进的加权k近邻算法所选择的最近邻参考点，其与测试点的物理距离排序与信号加权欧氏距离的排序基本一致。话句话说，信号加权距离越小代表物理距离也就越小。因此，使用加权欧氏距离可以提高指纹匹配的准确度，赋予最近邻参考点坐标更合理的权重，可提高位置估计的精度。

表3 两种加权k近邻算法的最近邻参考点选择和定位误差

为了验证所提出的算法能够显著提高定位精度，比较了3种基于不同距离度量的加权k近邻算法的定位误差：基于欧氏距离的加权k近邻算法、基于曼哈顿距离的加权k近邻算法和文中提出的基于加权欧氏距离的改进的加权k近邻算法。3种算法在选取不同数量的最近邻参考点下的平均定位误差如图5所示，选取的最近邻参考点个数等于4时的定位误差累计概率分布如图6所示。可以看出，所提出的改进的加权k近邻算法的定位误差明显小于其他两种算法的。

图5 不同最近邻参考点个数下的平均定位误差

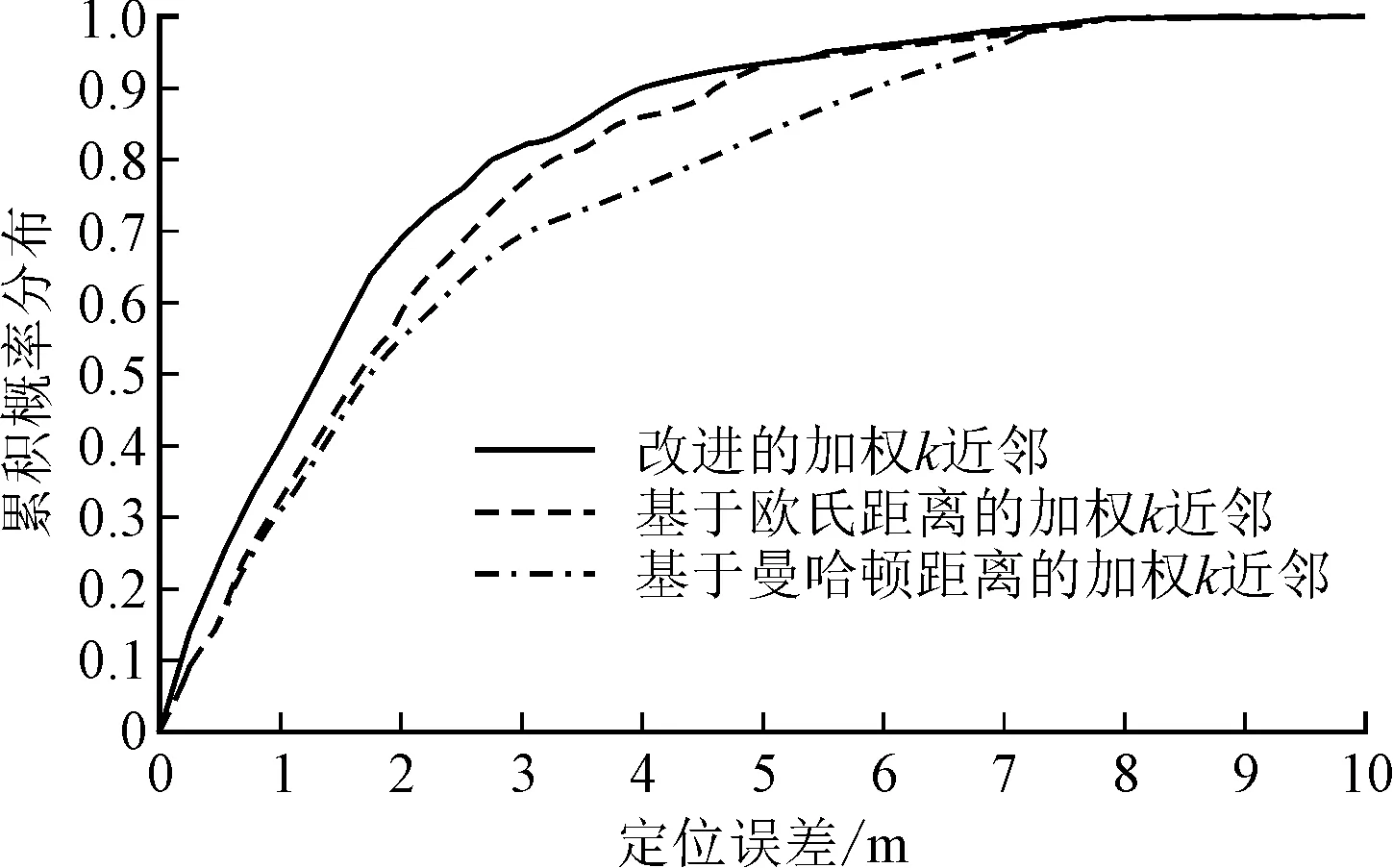
图6 最近邻参考点个数为4时定位误差累计概率分布

表4改进的加权k近邻算法和传统的加权k近邻算法的定位误差统计m

方法50%定位误差75%定位误差平均定位误差均方根定位误差改进的加权k近邻算法1.352.481.821.51基于欧氏距离的加权k近邻算法1.762.912.291.95基于曼哈顿距离的加权k近邻算法1.813.692.612.14

从表4列出的定位误差统计值中可以得出同样的结论，即相比于传统的基于欧氏距离和曼哈顿距离的加权k近邻算法，所提出的改进的加权k近邻算法具有更小的定位误差。相比于基于欧氏距离的算法，其平均定位误差提升了20.5%，均方根误差提升了22.6%。相比于基于曼哈顿距离的算法，其平均定位误差提升了30.3%，均方根误差提升了29.4%。

4 结束语

笔者通过分析室内WiFi信号的波动性,在信号距离计算中引入了接收信号强度方差，并根据WiFi信号的衰减特性给不同的接收信号强度差值分配权值，提出了一种改进的加权k近邻算法。实验结果表明，所提出的信号加权欧氏距离能够更准确地反映各位置点间的物理距离，提高了指纹匹配的准确度和定位精度。改进的加权k近邻算法的平均定位误差可达1.82 m，相比于传统的基于欧氏距离和曼哈顿距离的加权k近邻算法，其平均定位误差分别约提升了20.5%和30.3%，能够满足用户在室内的高精度定位需求。