地铁隧道施工引起邻近埋地管道位移计算的传递矩阵法

王海涛,金 慧,2,张景元,何 永,闫 帅

(1.大连交通大学 土木工程学院，辽宁 大连 116028; 2.北京交通大学 土木建筑工程学院，北京 100044；3.浙江铁道建设工程有限公司，浙江 杭州 310020)

盾构法隧道施工凭借施工扰动小、不影响城市交通等优点，成为城区内修筑地铁的主要建设方法之一。由于盾构开挖洞体和盾构衬砌结构之间存在一定的建筑间隙，尽管可以采用壁后注浆手段进行孔隙填充，但盾构掘进过程中仍会不可避免地扰动隧道周围土体，诱发地面和隧道上覆土体产生沉降和变形，进而引发邻近管道等埋地构筑物、建筑物受地层荷载作用而发生变形，严重时影响管道的正常使用功能，甚至爆裂诱发地层坍陷等严重事故。国内外学者针对隧道施工，采用模型试验、理论分析、数值模型和经验分析等方法对管道变形规律进行了较广泛的研究，并取得了一定的成果。理论研究的重点在于建立管道力学模型，研究隧道扰动区内地层外荷载与管道变形曲线的关系，研究成果可以较便捷地应用于实际工程，为实际施工控制与防护提供指导性建议。文献[1]在弹性地基梁模型基础上，采用能量法推导隧道在管道下方穿越时管道竖向位移的理论解析式，并在此基础上得到双线隧道穿越时管道竖向位移的解析解。文献[2]考虑地层中管道和土体的相互作用与弹性半空间上梁弹簧模型的差异，进一步考虑地层中管道埋深的影响，修正Winkler地基基床模量的计算公式。文献[3]考虑地层地基基床系数沿管道的不均均分布特性，认为管道沉降区和隆起区的地基基床模量存在一定差异，并给出参考取值，在此基础上推导出管道竖向变形的解析函数。文献[4]采用边界元思想，通过位移控制两阶段分析方法考虑具有不同土性的分层土体，研究隧道施工扰动区地层中管道的变形规律。文献[5]采用有限差分方法，在考虑土体分层效应的基础上，将柔性接口管道的接头简化为塑性铰，研究分层土体荷载作用下管道的力学响应。文献[6]采用Pasternak地基模型，考虑土弹簧间的剪切作用和埋深对地基反力模量的影响，修正水平受荷桩桩侧位移的计算方法，认为Pasternak地基模型在水平桩剪切模量较大土体侧向位移的测量精度上有一定的提高。文献[7]通过对管道变形规律的研究，同样认为Pasternak地基模型更适合应用于土体剪切模量较大的地层。在进行管道变形曲线微分方程求解时，往往求解规模大、过程繁琐复杂、待定参数较多，因此Pasternak地基模型难以直接应用于工程实际中。

针对以上不足，本文提出一种更为便捷且精确的管道竖向位移计算方法。将管道视为Winkler地基上的弹性地基梁，采用两阶段分析方法，分别对地层沉降函数和管道变形函数进行傅里叶级数展开，推导出地层沉降和管道变形间的力学关系，并定义位移传递矩阵，提出基于地层沉降的管道位移预测公式；同时对影响管道位移的相关参数进行分析，建立综合考虑多种影响因素的埋地管道最大位移预测公式，以期为地铁隧道施工安全控制与防护提供参考。

1 位移传递矩阵法

1.1 计算模型

隧道下穿管道计算模型如图1所示。假定地层为均一土性地层，隧道垂直下穿既有管道，地层中管道埋深为zp，隧道开挖半径为R，隧道轴线位置埋深为h，地层中未埋设管道时管道埋深处地层受隧道开挖扰动产生的最大沉降为Smax(x)，管道变形范围计算长度的一半设为l，经计算，当l取20R时可以满足计算精度要求。本文仅就土体竖向沉降对管道竖向变形的影响进行研究，忽略管道接头处刚度的折减效应，认为埋地管道为刚度连续的地基梁结构。

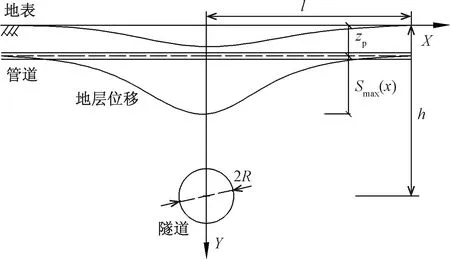
图1 隧道下穿管道计算模型

1.2 地层沉降和管道位移傅里叶变换

通过傅里叶变换可将任意地层沉降函数表示为三角函数叠加的形式，通过求解三角函数形式地层荷载作用下的管道变形，即可将隧道施工时复杂模式的地层沉降作用下管道变形问题转化为可求解问题。文献[8]通过理论分析推导出隧道开挖扰动下周围土体的竖向位移解析公式，见式(1) ，本文将式(1)作为盾构施工扰动产生的地层沉降函数进行管道变形的求解。

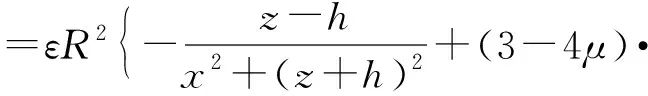
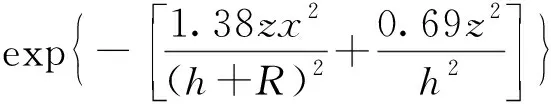
(1)

式中：S(x)为地表以下深度z处的地层沉降函数，m；x为计算点与隧道轴线间的水平距离，m；μ为地层内土体泊松比；ε为隧道施工产生的地层损失率。

设管道位移函数为Sp(x)，对地层沉降函数和管道位移函数进行傅里叶级数展开，并分别表示成向量相乘的形式，即

S(x)=XTb

(2)

Sp(x)=XTa

(3)

式中：向量X中的各个元素为傅里叶级数展开式的基函数；向量b和a中各个元素为对应基函数的常系数。

bn(n取0～20)可通过式(4)进行计算求取，当展开项数n值达到10时，第n项基函数所对应的常系数已经非常小，但为了保证计算精度要求文章中n取值为20。

(4)

1.3 管道位移的传递矩阵法求解

两阶段分析方法是目前解析隧道施工对埋地管道变形影响的主要方法之一，其研究思路分为两步：第一步，不考虑地层中埋设的管道，直接计算未埋设管道土体在隧道施工扰动下的地层沉降S(x)；第二步，把地层假设为地基弹簧，通过地基基床反力模量，把上述地层沉降转化为地层荷载并作用于管道上，在上述地层荷载和地层反力作用下，管道完成与土体的变形协调，即实际上管道和土体发生的共同位移Sp(x)。基于上述管道和土体的相互作用过程，通过Winkler地基模型构建管道变形平衡微分方程

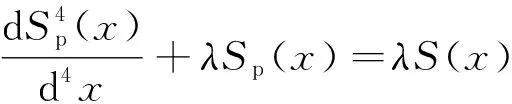
(5)

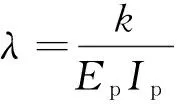
(6)

式中：λ为埋地管道相对于土体的柔度系数；k为隧道周围土体地基基床反力模量，kN/m2；Ep为管道的弹性模量；Ip为管道的截面惯性矩。

考虑到管道在地层中有一定的埋深，与弹性半空间上的梁弹簧模型存在差异，故本文采用文献[2]推导出的考虑管道埋深影响的Winkler地基基床反力模量的修正公式

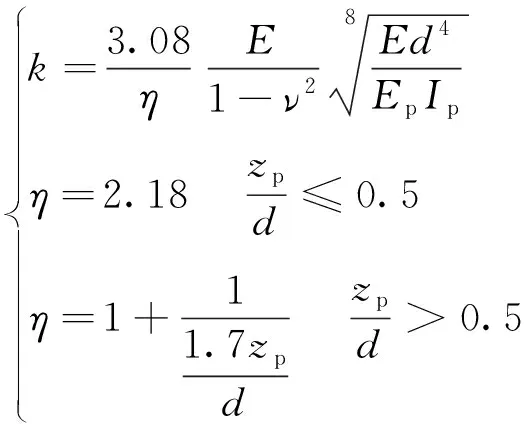
(7)

式中：ν为管道所在位置土体的泊松比；E为管道所在位置土体的弹性模量；d为管道直径；η为管道埋深修正系数。

将式(2)、式(3)代入式(5)，整理得

X(4)T+λXTa=λXTb

(8)

通过计算整理得

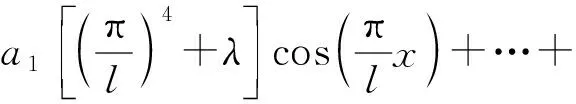
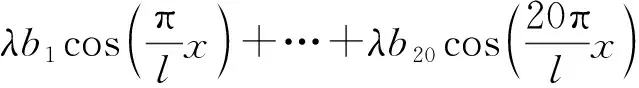
(9)

要保证式(9)成立，等号两侧各项基函数的常系数应对应相等，则可以整理得到一组方程，见式(10)，将该方程组用矩阵形式表示得式(11)。

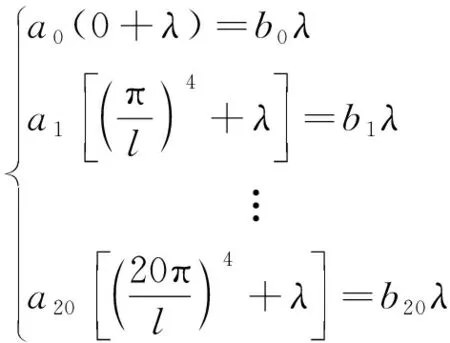
(10)

(11)

为描述土体位移与管道位移之间的相互作用和传递关系，定义式(11)中的对角矩阵为位移传递矩阵K，则式(11)可进一步表示为式(12)。在地层沉降常系数向量b和传递矩阵K已知的情况下，可直接求解得到管道位移常系数向量a。将式(12)代入式(3)，进行矩阵运算可得到近似的管道位移函数，见式(13)。

Ka=b

(12)

Sp(x)=XTK-1b

(13)

可利用Matlab软件进行编程，快速计算求解。

2 算例验证

2.1 现场实测

文献[9]经现场实测对某沿海城市软土地区地铁隧道工程引起地层及管道的变形情况进行深入研究，隧道参数如下：隧道外径为6.2 m，内径为5.5 m，埋深为15.12 m；地下有多种管道密布，将球墨铸铁材质煤气管道作为分析对象，其直径为0.3 m，埋深为0.9 m，抗弯刚度为15.2 MN·m2，管轴线与隧道轴线的相交角约为88°，可以近似认为管道与隧道正交。经勘测，地层主要由饱和黏性土、粉性土和砂性土组成，管道所在土层的参数：土体弹性模量取上覆土层的加权平均值4.44 MPa，泊松比为0.3，文献[10]对此类工程进行了统计分析，结果显示类似工程的地层损失率通常小于5‰，故本文选取地层损失率为5‰进行计算。

图2为本文计算方法与实测结果的对比。从图2可以看出，虽然本文方法的最大下沉位移较实测结果偏大，管道的上升位移较实测偏小，但管道沉降槽形状较接近实测，二者变形特性基本相符。差异的可能原因是：管线所在土层为人工素填土，土质情况较差，计算时高估了土质条件，导致管道相对于土体的柔度系数偏大，抗弯能力较差，因此出现管道下沉位移值偏大，没有明显上升变形的现象。

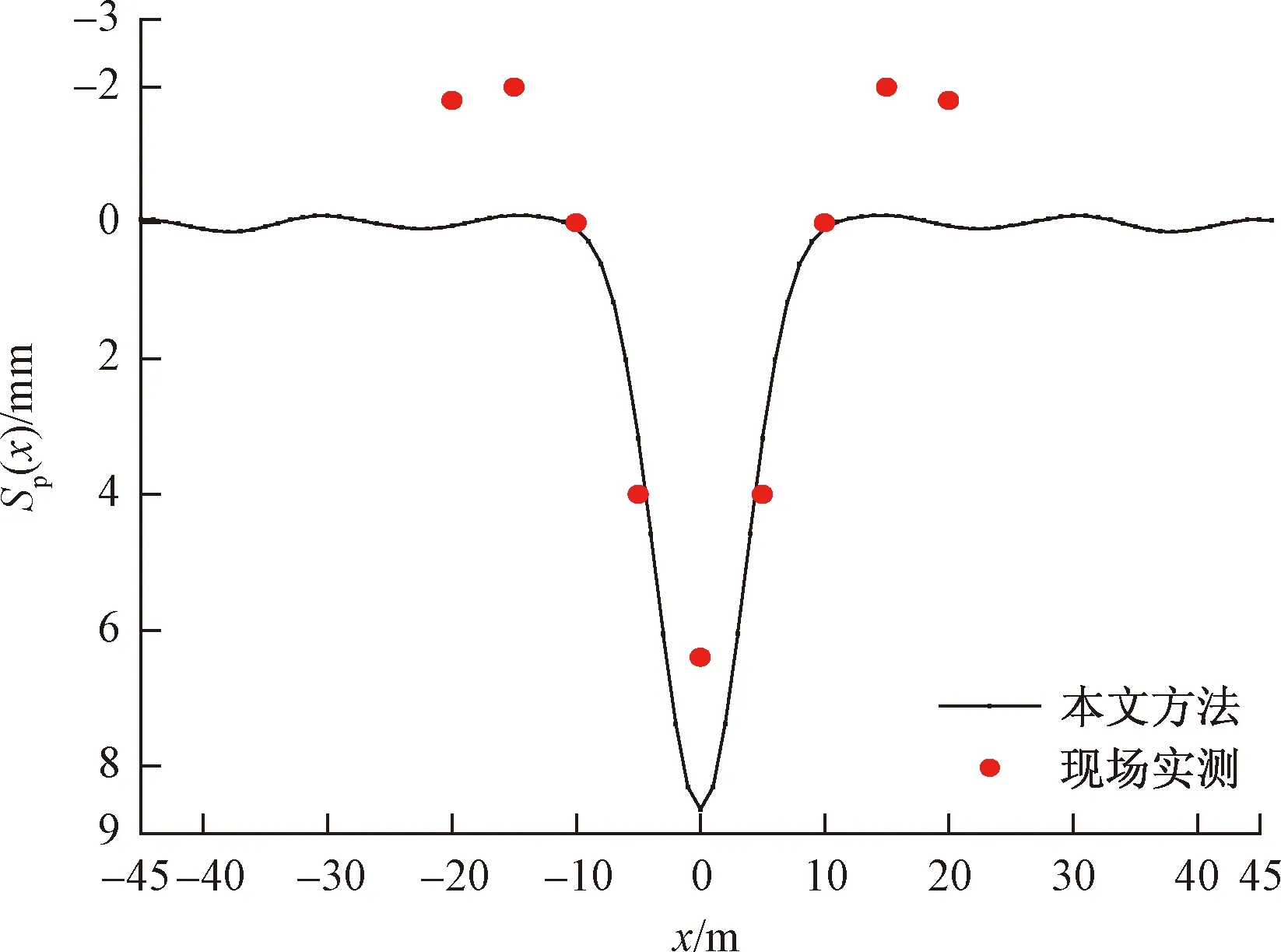
图2 本文计算方法与现场实测对比

2.2 模型试验

文献[11]通过开展离心模型试验，监测加速度取75g时几种不同地层损失率管道的变形规律。选取地层损失率为2%时的一组试验数据与本文理论计算结果进行对比分析。通过相似比换算得到原型试验对应的参数：砂土弹性模量为19.52 MPa，砂土泊松比为0.3；隧道直径为4.5 m，隧道轴线埋深为11.25 m；管道直径为1.19 m，管道截面刚度为3 363 MN·m2，管道埋深为4.165 m。

图3为本文方法计算结果与试验数据的对比图。从图3可以看出，本文方法可以精确地反映试验中管道的变形规律，进一步验证了本文方法的可靠性。

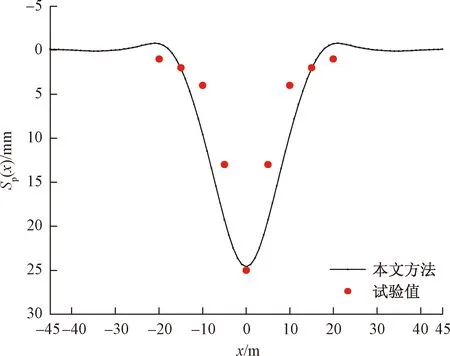
图3 本文计算方法与试验对比

3 因素分析

3.1 管道埋深

基于2.1节实例，对不同埋深对管道位移的影响情况进行分析，见图4。从图4中可以看出，管道埋深对管道位移和管道沉降槽宽度的影响并不明显，原因可能有以下两点：其一，通过对管线所在地层位移的计算发现地层位移随埋深增加而产生的增量较小；其二，随着管道埋深的增加，土质条件变好，管道相对土体的刚度减小，柔度增大，抗弯能力减弱。为描述这一特征，基于本文理论，对管道最大位移Sp,max与管道埋深的关系进行曲线拟合，见图5，可以看出拟合曲线斜率较小。

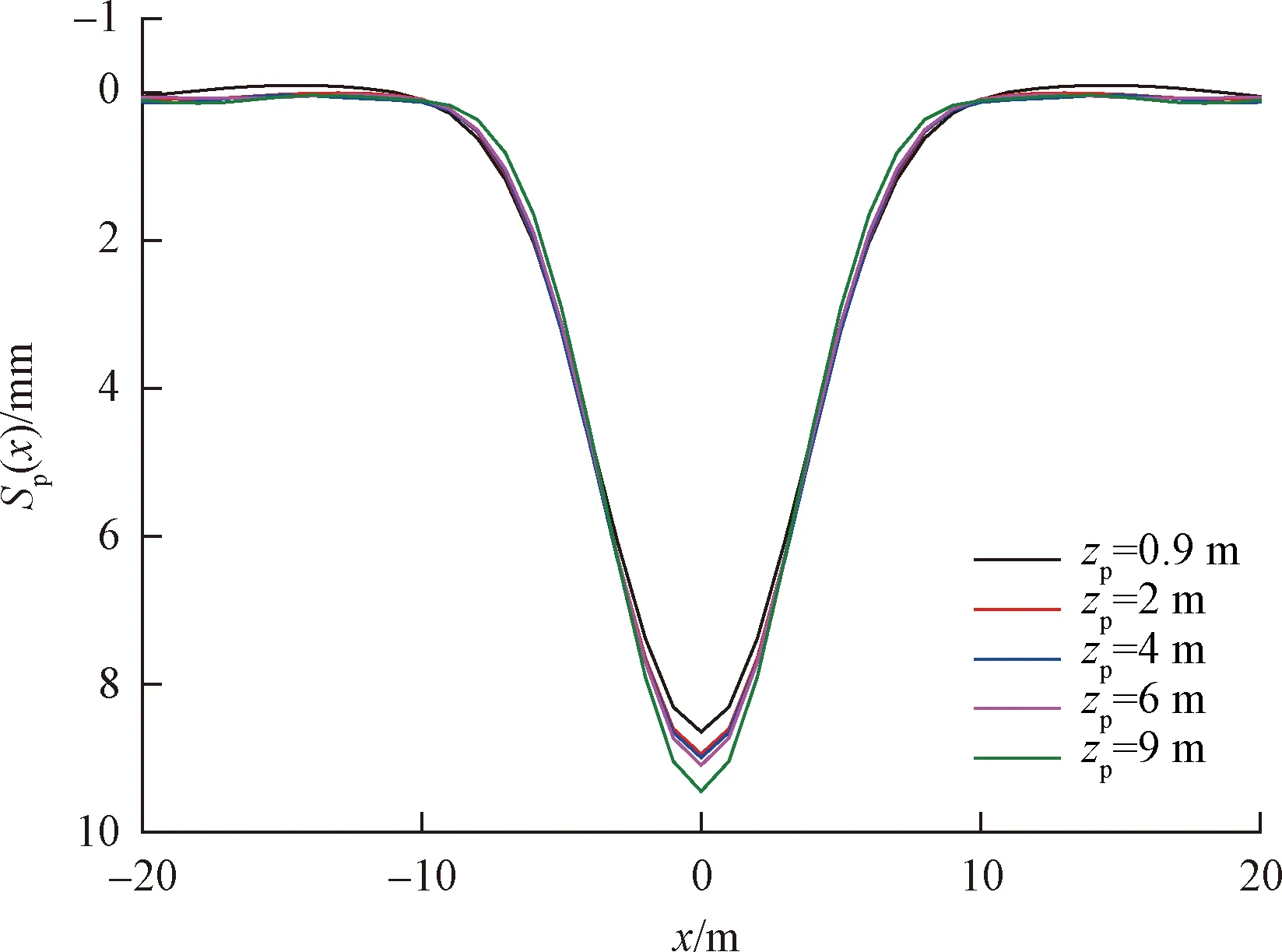
图4 管道埋深对管道位移的影响

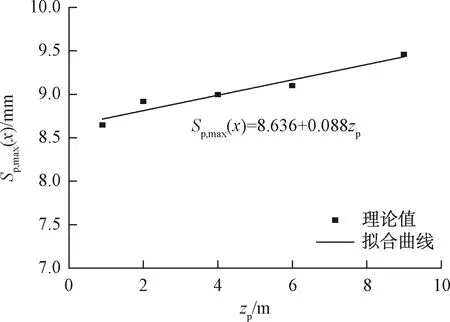
图5 管道最大位移与管道埋深的关系

3.2 管道刚度

基于2.1节实例，假设管道截面直径不变，以钢管、混凝土管道、PVC-U管道等为模型基础，对不同截面刚度的管道进行分析研究，见图6。从图6可以看出：管道最大位移随管道截面刚度的增加而减小，管道沉降槽宽度随管道截面刚度的增加而增大，同时，随着截面刚度的增加，沉降槽开口位置处管道的上拱现象更加明显，且上拱范围明显增大。通过对管道最大位移理论计算值与管道截面刚度的相关性进行拟合，得到管道最大位移关于管道截面刚度的预测曲线，见图7。实际工程中，不同用途的管道其材质、直径、管壁厚度等参数均有所不同，本文仅对直径0.3 m管道进行了说明，借助本文方法，可以对不同截面尺寸、相同材质管道进行规律性分析研究，以便对地铁隧道施工进行设计指导。

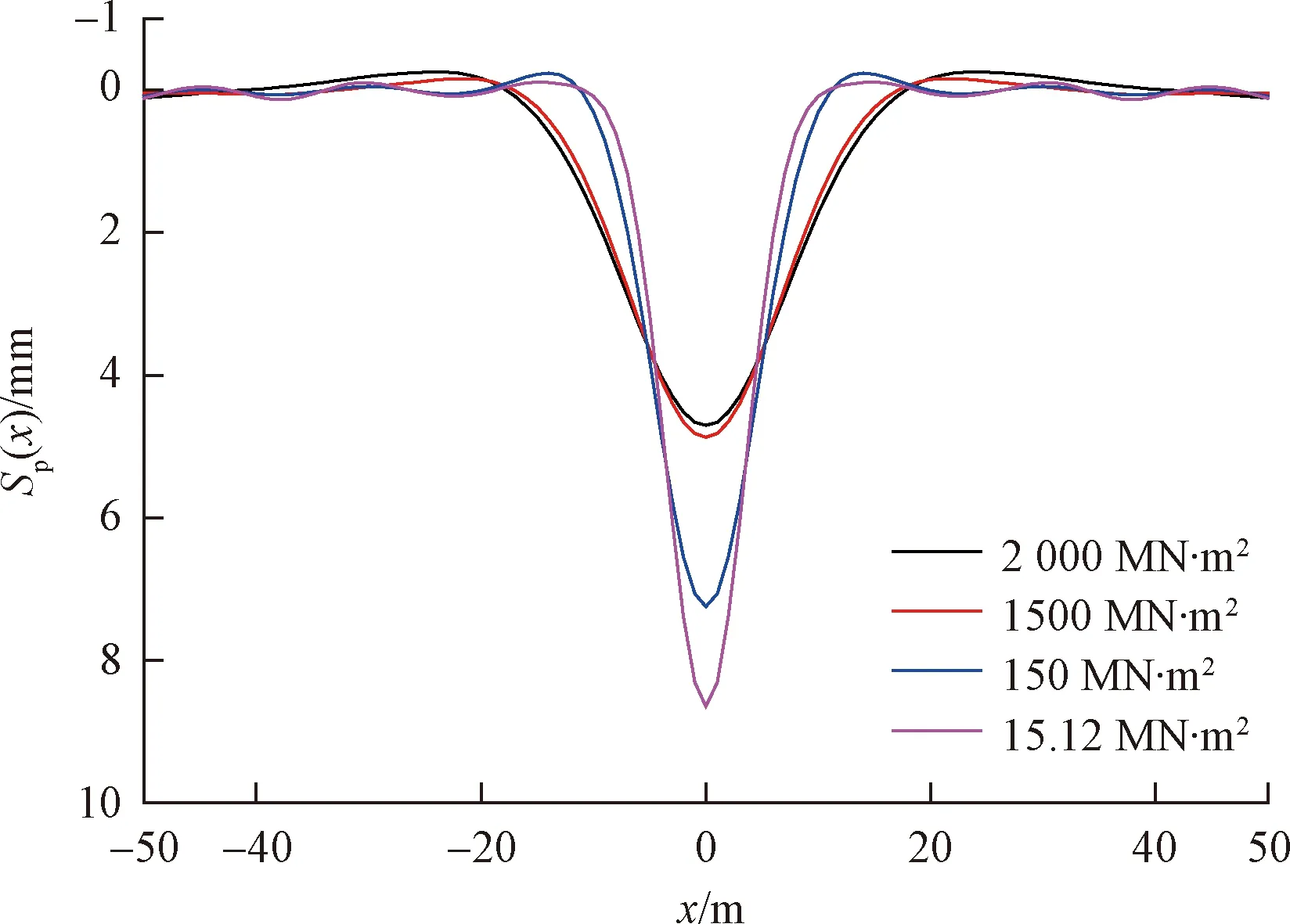
图6 管道截面刚度对管道位移的影响

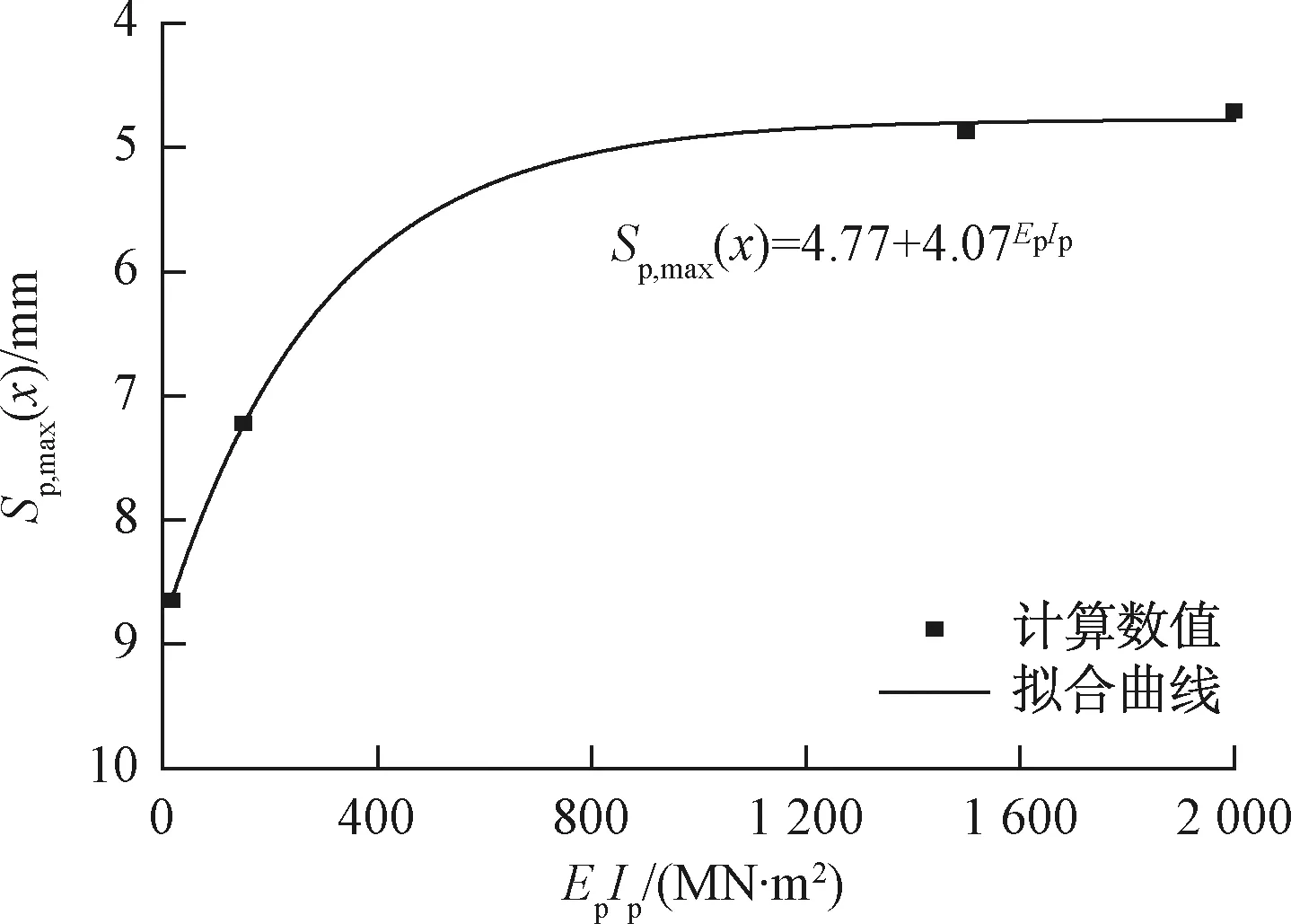
图7 管道最大位移与管道截面刚度的关系

3.3 土体损失率

基于2.1节实例，对不同地层损失率时的管道位移进行分析研究，见图8、图9。从图8、图9可以看出：地层损失率对管道位移的影响较明显，在隧道埋深和半径不变的情况下，管道最大位移与地层损失率近似呈正比例增长关系。其原因可能是实例中管道的刚度较小，管道位移模式主要受地层位移模式控制，在地层位移较大时，管道表现出较弱的抗弯能力，因此控制隧道施工诱发的地层损失对控制管道位移是至关重要的。

图8 管道位移与地层损失率的关系

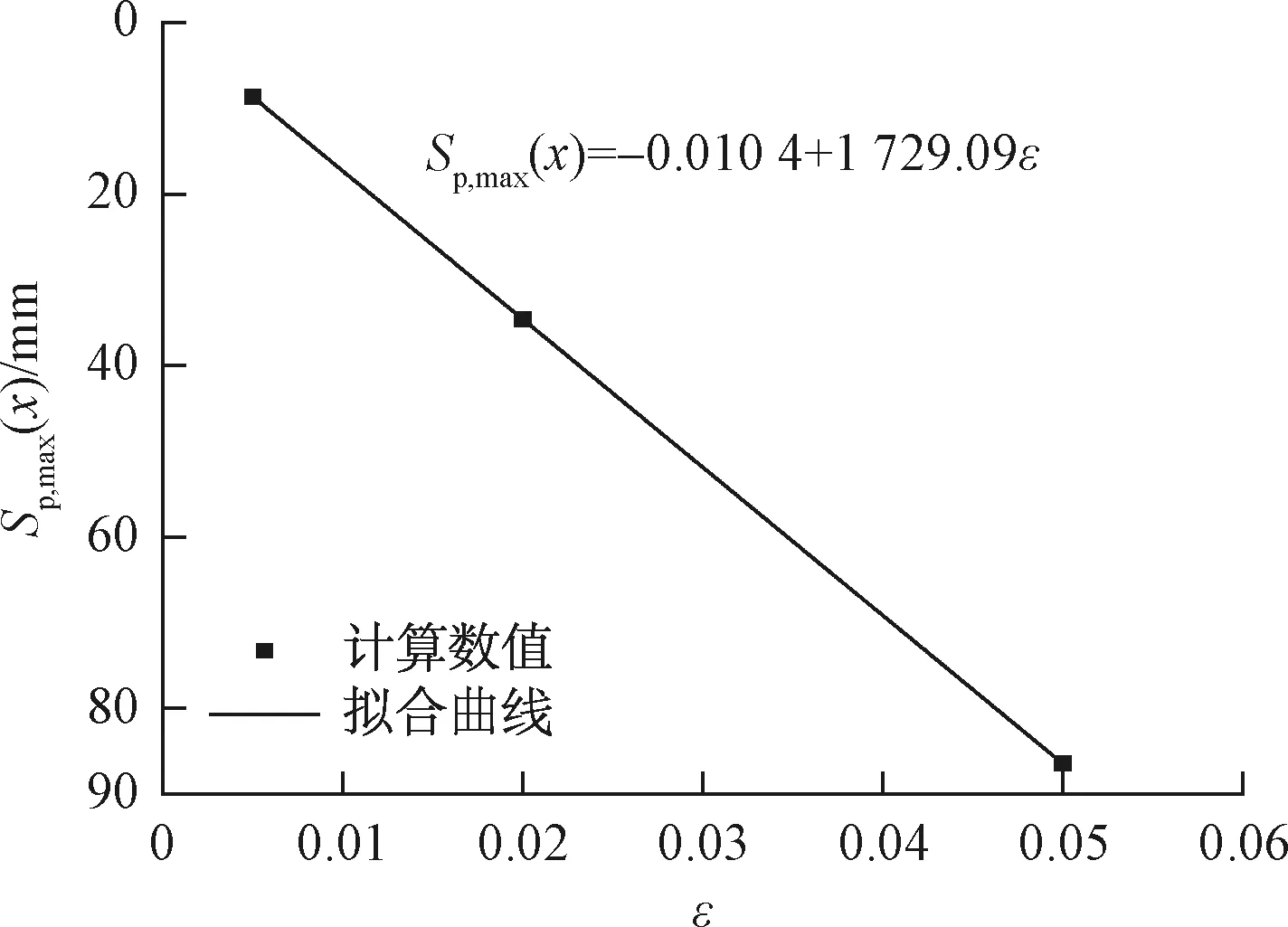
图9 管道最大位移与地层损失率的关系

3.4 管道最大位移值与管道相对柔度系数的关系

管道位移规律是多种影响因素综合作用的结果，因此某单一因素引起的变化规律在工程应用中有一定的局限性。由以上分析可知管道相对柔度是管道截面刚度、截面尺寸、管道埋深、土体弹性模量、泊松比等因素在管道相对抗弯刚度上的综合反映，管道埋深处地层位移是隧道埋深、隧道半径、地层损失率等因素在管道附加荷载大小上的综合反映，为全面考虑多因素影响下的管道位移变化规律，定义最大位移传递系数Kmax，见式(14)，同时，通过对理论计算值λ与Kmax的统计分析，建立最大位移传递系数关于管道柔度系数的预测式，见式(15)、图10。可知当λ→0时，管道刚度趋于无穷大，管道位移趋于0，Kmax→0；当λ→∞时，管道与土体协调变形，不存在相互作用，管道位移趋于地层位移，Kmax→1；当λ∈(0，∞)时，Kmax呈对数分布，事实上，当λ→0.84时，就有Kmax→1。

Kmax=Sp,max/Smax

(14)

Kmax=1.012+0.068ln(λ-0.001)

(15)

图10 Kmax与λ关系

为进一步验证式(15)的可靠性，对2.2节实例中最大位移传递系数进行了计算，见图10中红点，计算值基本与理论值吻合。本文提出的预测公式可以综合反映不同地质条件、隧道埋深及直径、管道材料及截面特性等多种因素影响下，管土相互作用强弱对管道位移与地层位移传递关系的影响，实现了地铁隧道施工引起邻近埋地管道最大位移的超前预测。

4 结论

(1)本文考虑管道埋深对地基基床反力模量的影响，修正了Winkler地基模型，采用两阶段分析法和傅里叶变换，推导出地层沉降与管道变形间的力学关系，并定义了位移传递矩阵，提出了基于地层沉降的管道位移预测公式。

(2)通过算例分析，将本文理论计算结果与现场实测和模型试验进行对比，理论计算结果与现场实测和模型试验数据吻合良好，证实了本文方法具有较高的精度。

(3)通过对管道埋深、管道截面刚度和地层损失率对管道位移影响的分析，认为在一定范围内，管道位移与管道埋深和地层损失率线性正相关，与管道截面刚度呈斜率逐渐减小直至趋于零的指数函数关系；在此基础上，定义了最大位移传递系数，建立了综合考虑多因素影响的管道最大位移预测公式。