考虑齿轮传动系统的重载电力机车轴重转移研究
王自超,陈再刚,翟婉明,张 杰,王开云
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都 610031; 2. 中国铁路设计集团有限公司,天津 300308)
黏着利用率对重载电力机车的动力学性能有直接的影响。机车牵引做功时,其动力输出从电机传至轮对,依靠轮对与轨道间的静摩擦产生牵引力驱动机车运动,在力的传递过程中,转向架各车轴的轴重分配(施加在车轴上的载荷)相对于静态轴重,会发生瞬时变化,有的增大,有的减小,这种现象叫做轴重转移。轴重转移会对重载机车黏着利用率造成较大影响。我国DF系列等早期型号的内燃机车,在某些特殊工况下,机车轴重转移达到了20%以上,这对机车的牵引效率造成了严重影响。机车轴重转移产生的根本原因是由于动力传递过程中牵引电机、齿轮啮合等产生的力与力矩作用,而且轴重转移的大小与转向架的结构形式和电机的布置方式有关[1]。
20世纪中期,国内外学者纷纷展开了机车轴重转移的理论研究。例如,瑞士Borgeau等[2]基于数学分析法研究了机车轴重转移特性,并提出了相应的轴重转移补偿技术。孙翔[3]分析了衡量机车轴重转移特性的相关指标,获得了轴重转移计算公式。陈大瀛等[4]在分析了DF(东风)型内燃机车的轴重转移情况后,提出了机车轴重转移的近似解和精确解两种方法。易理明等[5]计算了SS3(韶山)型电力机车的轴重转移结果,通过改进并简化常用的理论分析方法,重新对机车动力学参数和牵引力变化情况下,机车轴重转移的直接表达式进行了推导。龚积球等[6]综合分析了各种理论计算方法求得的机车轴重转移结果,在此基础上提出了轴重转移极限值。陈石华等[7]以某2(B0-B0)轴式机车为例,提出了八轴机车轴重转移的数值计算模型。王珏等[8]基于空间耦合动力学理论研究了机车轴重转移特性,分析了变速工况以及二系纵向刚度的影响,获得了牵引电机在车体半悬挂方式下的轴重转移特性。吴安伟等[9]建立了精确的数学计算模型,并对某B0-B0-B0型电机轴悬式机车的轴重转移进行了计算,结果表明,机车的最佳黏着利用率出现在名义牵引点与最佳牵引点等高工况。杨勇军等[10]对DF、CKD、DF型机车在坡道上的轴重转移进行了计算,采用的方法包括精确法和简化法,结果表明,坡道对机车轴重转移的影响很小,当坡道上的车钩牵引力与直线上的车钩牵引力相同时,机车轴重转移会略有增加。罗洪文等[11]推导了2(B0-B0)轴式机车轴重转移的理论计算模型,进而研究了转向架轴距、牵引点高度、悬挂系统刚度等对黏着利用率的影响。王艳等[12]通过分析C0-C0电机轴悬式机车轴重转移结果,研究了牵引传动系统悬挂方式对机车轴重转移的影响,结果表明,牵引传动装置的布置方式对C0-C0轴悬式机车的轴重转移影响较大,如果牵引传动装置布置方式不合理,机车的黏着利用率可能低于90%。伍泓桦等[13]对33 t轴重的电力机车轴重转移进行了分析,采用的方法包括多体动力学和数值分析法,分析了悬挂系统参数、牵引点高度及悬挂形式对机车轴重转移的影响。
在计算机设备发展成熟之前,国内外针对各种类型的机车轴重转移,大多只能采用静力学的方法研究[14]。随着计算机软硬件的进步,近年来采用多体动力学的方法进行机车轴重转移的研究越来越多,但这些研究大都存在一个共同的缺点——简化了牵引传动系统,忽略齿轮传动装置内部动态激励的影响,未考虑电机动力通过齿轮传动装置传至轮对的过程[15]。Chen等[16-17]建立了一种包含传动系统的机车-轨道垂向耦合动力学模型,对齿轮装置内部激励对机车动力学性能的影响进行了分析,研究表明,轮轨接触激励和齿轮啮合激励对机车-轨道耦合动力学系统具有不同程度的影响。综上所述,在机车轴重转移的研究中,考虑牵引传动装置的齿轮啮合过程以及传动系统的内部动态激励,是非常有必要的。
机车牵引传动系统的主要激励源包括齿廓误差、时变啮合刚度、齿面振动冲击,开展这方面研究工作的学者越来越多。Chen等[18]、Shao等[19]建立了一种齿轮时变啮合刚度分析模型,并以此为基础建立了齿根裂纹故障计算模型,指出,机车牵引传动系统动态响应的另外一个主要激励源是齿形误差,为了计算齿根裂纹及齿廓修形对齿轮时变啮合刚度的影响,又建立了齿轮时变啮合刚度与齿形误差相互影响的计算模型[20]。
基于上述分析,本文在某型重载电力机车多体动力学模型中,引入了完整的齿轮传动系统。该模型能够准确地仿真机车动力传递过程,尤其适用于变速变载等复杂工况下的机车及其传动系统动力学仿真分析。此外,由于充分考虑了齿轮箱内部的齿轮啮合过程,该模型还可用于揭示内部、外部动态激励同时作用下的车辆系统与传动系统之间的动态相互作用,为研究机车实际运行过程中的瞬时轴重转移奠定了基础。
1 重载机车-齿轮传动系统动力学模型
为研究牵引传动系统对机车轴重转移的影响,进而分析轮齿系统对机车动力学性能的影响,本文采用SIMPACK多体动力学软件建立了完整的含有齿轮传动系统的重载机车动力学模型,齿轮传动系统模块基于SIMPACK软件包中的225:Gear Pair力元,该力元可以对齿轮副的阻尼、摩擦、变位、啮合刚度等进行详细建模;在求解过程中,使用软件包自带的SODASRT 2积分方法。机车动力学模型如图1所示,其主要悬挂参数如表1所示。图2为建立的对称布置轴悬式牵引传动装置模型,其齿轮传动设计参数如表2所示。图3所示为该型机车的牵引特性曲线。

图1 机车动力学模型
需要指出的是,本文研究的机车齿轮传动系统中齿轮副属于变位齿轮,相对于标准齿轮,变位系数将通过改变齿轮啮合刚度从而影响齿轮传动系统动态特性[21]。因此,本文建立的机车动力学模型也考虑了齿轮变位系数对时变啮合刚度激励的影响。
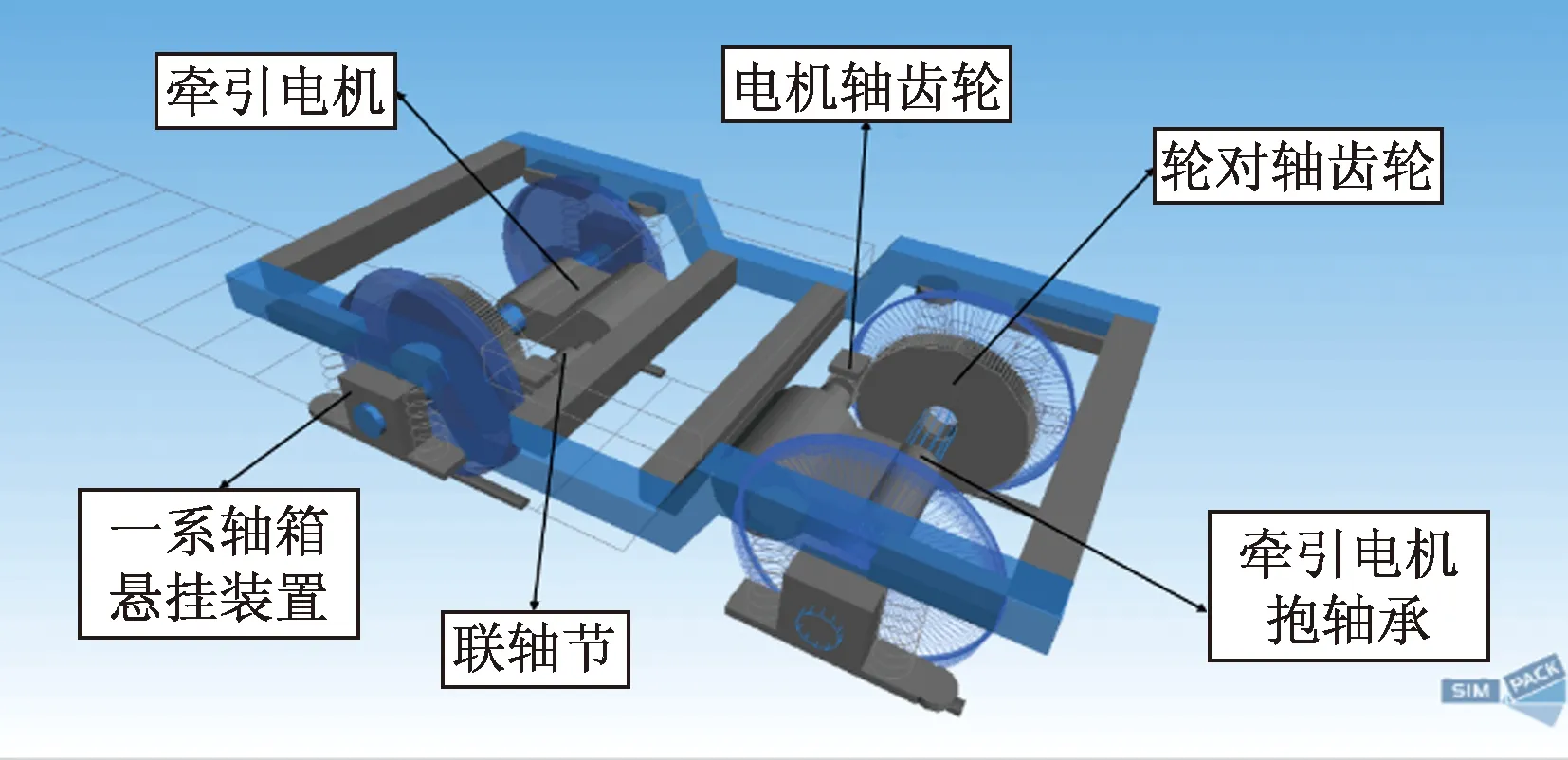
图2 机车齿轮传动系统动力学模型

图3 机车牵引特性曲线
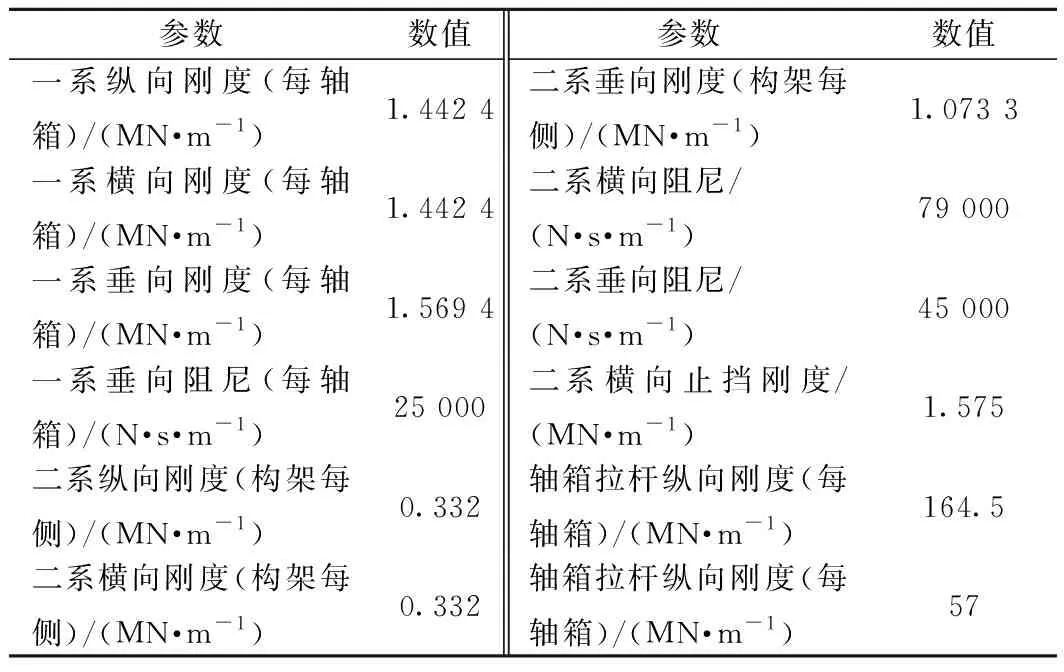
参数数值参数数值一系纵向刚度(每轴箱)/(MN·m-1)1.442 4二系垂向刚度(构架每侧)/(MN·m-1)1.073 3一系横向刚度(每轴箱)/(MN·m-1)1.442 4二系横向阻尼/(N·s·m-1)79 000一系垂向刚度(每轴箱)/(MN·m-1)1.569 4二系垂向阻尼/(N·s·m-1)45 000一系垂向阻尼(每轴箱)/(N·s·m-1)25 000二系横向止挡刚度/(MN·m-1)1.575二系纵向刚度(构架每侧)/(MN·m-1)0.332轴箱拉杆纵向刚度(每轴箱)/(MN·m-1)164.5二系横向刚度(构架每侧)/(MN·m-1)0.332轴箱拉杆纵向刚度(每轴箱)/(MN·m-1)57
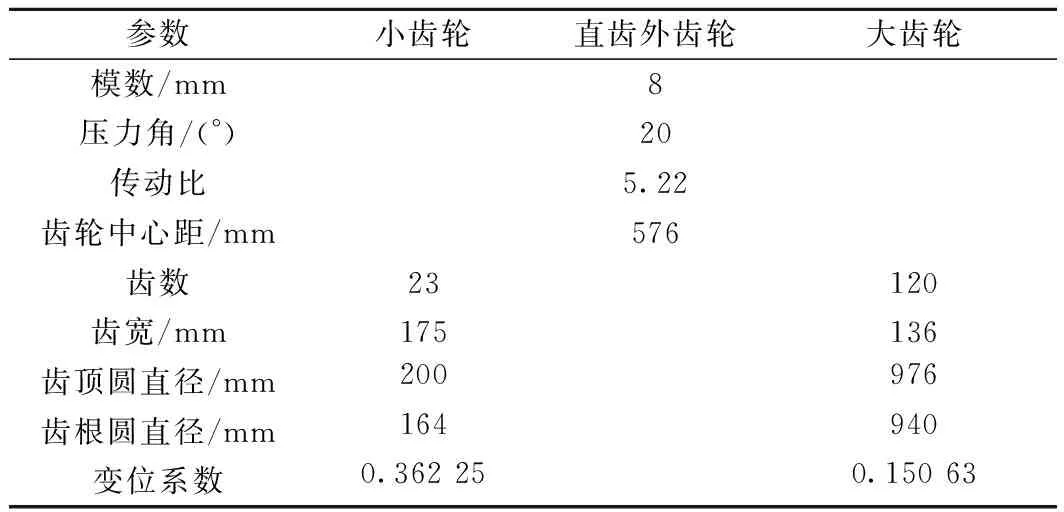
表2 齿轮传动设计参数
2 机车轴重转移理论解析计算模型
传统轴重转移计算中忽略了牵引动力经齿轮传动系统传递过程的影响,本节在文献[1]中的方法基础上,详细考虑了牵引动力通过齿轮传动系统传递的影响,进一步改进了机车轴重转移的理论计算方法,推导了轴重转移解析计算公式,其能够准确地反映机车轴重转移的特性与规律。
该型机车为重载货运电力机车,轴重约为25 t,轴式为2(B0-B0),牵引传动装置采用轴悬式对称布置,通过抱轴承及吊杆分别与车轴和构架相连,如图4所示,图中模型参数见表3。
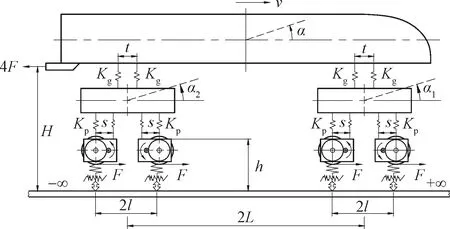
图4 机车轴重转移计算分析模型

参数数值转向架轴距之半l/m1.300二系圆簧间距t/m0.360转向架中心距L/m5.030轮径D/m1.250二系左右两圆簧垂向刚度Kg/(kN·m-1)1 073.3一系每轴箱圆簧垂向刚度Kp/(kN·m-1)3 138.8车钩中心线距轨面高度H/m0.880牵引电机转矩T/(kN·m)10.925电机悬挂点距车轴中心距s/m1.110牵引点高度h/m0.800
设ΔP1~ΔP4为第1轴至第4轴每轴轴箱圆簧的增载量;ΔR1~ΔR4为每轴轴重转移,其中ΔRi为正表示减载,为负则表示增载;ΔG1~ΔG4为转向架左右两个圆簧之和的增载量;而α、α1、α2则分别为车体以及前、后构架的倾角。根据转向架一系、二系圆簧的变形条件,可以得到方程
ΔP2=ΔP1+2Kplα1
(1)
ΔP4=ΔP3+2Kplα2
(2)
图5为车体与前后构架的几何关系示意图,由该图可以得到方程
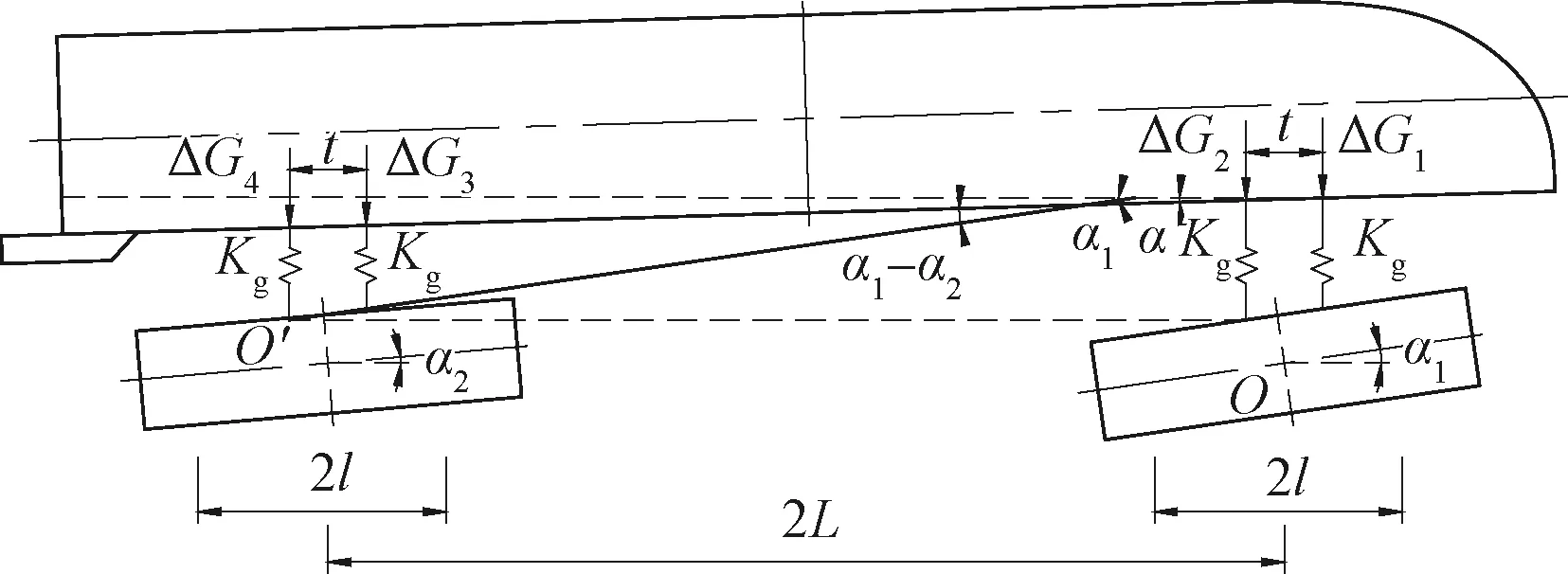
图5 车体及构架受力变形的几何关系
(3)
ΔG3=ΔG1-[(ΔP3-ΔP1)/Kp-
(l-t/2)(α1-α2)-2Lα]Kg
(4)
ΔG4=ΔG1-[(ΔP3-ΔP1)/Kp+t(α2-α)-
(l-t/2)(α1-α2)-2Lα]Kg
(5)
且有
ΔR1=ΔP1+ΔQ1
(6)
ΔR2=ΔP2+ΔQ2
(7)
ΔR3=ΔP3-ΔQ3
(8)
ΔR4=ΔP4-ΔQ4
(9)
对各主要部件进行受力分析,分析过程如图6、图7所示。
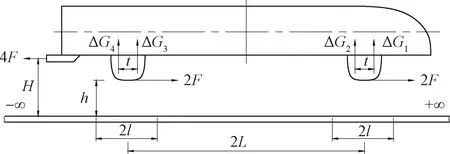
图6 车体受力分析示意图
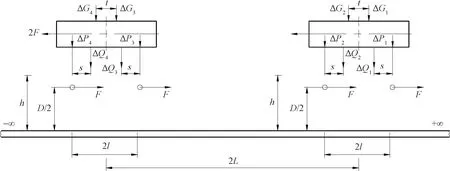
图7 构架受力分析示意图
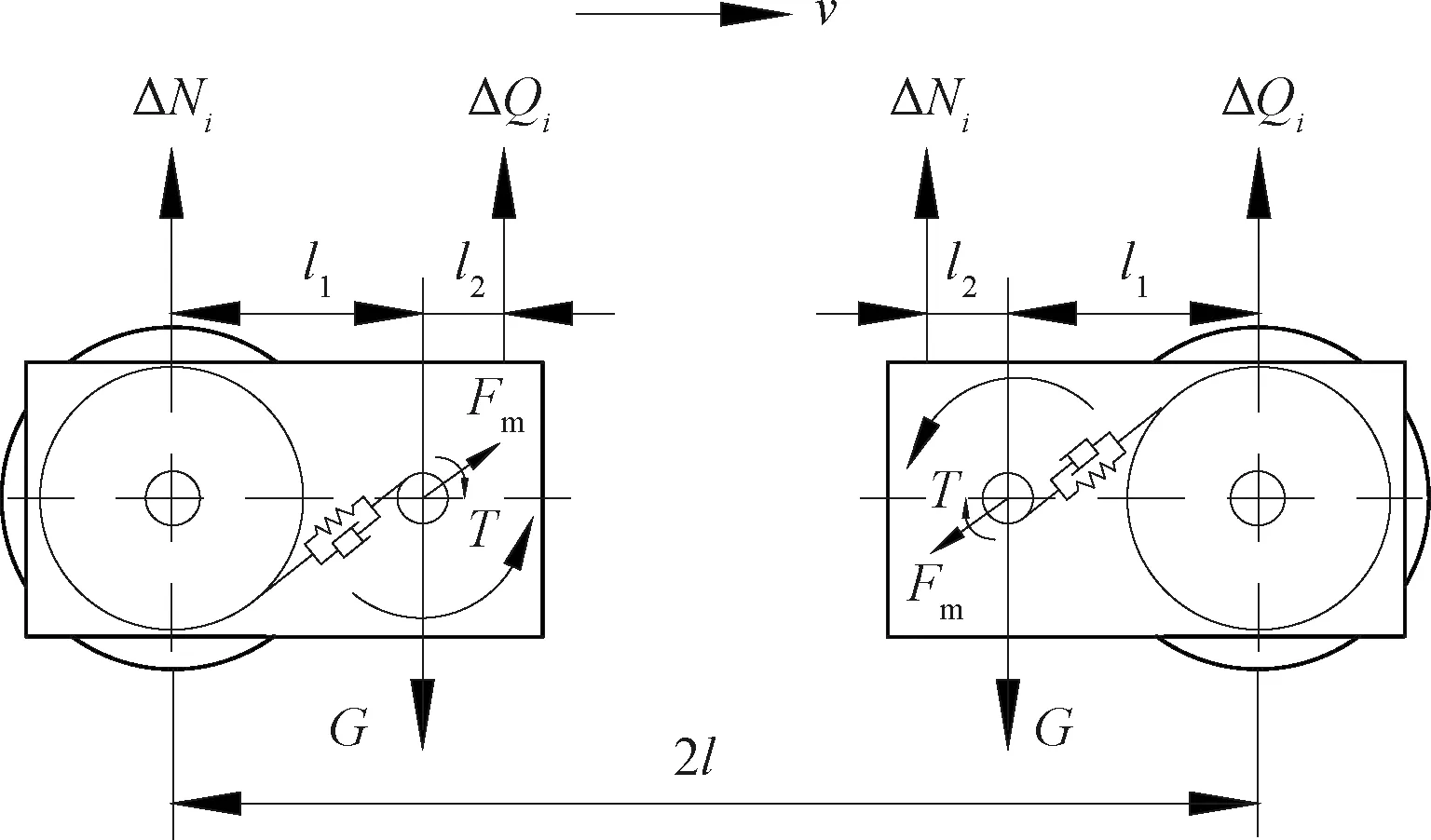
图8 齿轮传动影响下的牵引电机受力分析示意图
根据车体受力分析可以得到方程
ΔG1+ΔG2+ΔG3+ΔG4=0
(10)
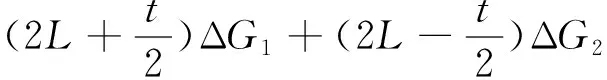
(11)
根据前构架受力分析可以得到方程
ΔG1+ΔG2+ΔP1+ΔP2+ΔQ1+ΔQ2=0
(12)
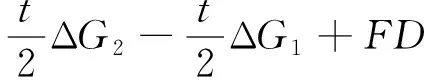
(13)
根据后构架受力分析可以得到方程
ΔG3+ΔG4+ΔP3+ΔP4-ΔQ3-ΔQ4=0
(14)
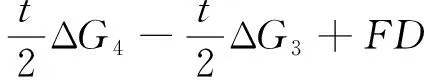
(15)
根据牵引电机受力分析,可以得到以下力平衡方程
ΔN1+ΔQ1-Fmsinαn-G=0
(16)
ΔN2+ΔQ2+Fmsinαn-G=0
(17)
ΔN3+ΔQ3-Fmsinαn-G=0
(18)
ΔN4+ΔQ4+Fmsinαn-G=0
(19)
ΔNi·l1+ΔQi·l2=0i=1,2,3,4
(20)
Fm=T/r
(21)
式中:Fm为齿轮啮合力;r为小齿轮基圆半径;αn为压力角;G为电机重力。
由此可见,方程式(1)~式(15)共15个,而未知数也为15个,因此,将这些方程改写成AX=B的矩阵形式,通过输入已知机车力和结构相关参数,可求解获得所有未知数的精确值。
3 考虑齿轮传动的机车轴重转移与理论解析计算结果对比分析
本节基于某型HX重载电力机车动力学参数,利用推导获得的机车轴重转移理论解析计算方程,以及建立的考虑齿轮传动系统的重载机车动力学模型对机车轴重转移进行了计算与仿真分析。
在准静态工况下(速度为5 km/h),采用本文推导获得的轴重转移理论解析计算方法获得的机车轴重转移结果,如表4所示。
表4 机车轴重转移理论解析计算结果(5 km/h)

轴号 1 23 4载荷/kN-22.598+21.541-21.541+22.598转移率/%-9.2+8.8-8.8+9.2
为了进一步解释齿轮传动系统对轴重转移的动态影响规律,仿真和计算了机车从静止分别加速至40、60、80、100 km/h共4种工况下的动态响应以及轴重转移,结果表明,4种工况下两种方法获得的机车轴重转移规律类似。表5为机车从静止加速至80 km/h的理论解析法计算结果。
表5 机车轴重转移理论解析计算结果(80 km/h)

轴号12 34载荷/kN-12.85+12.24-12.24+12.85转移率/%-5.2 +5.0 -5.0+5.2
相同工况下,即机车从静止加速至80 km/h,考虑齿轮传动系统动态影响下的机车运行速度时程曲线如图9所示。由图9可以看出,本文建立的考虑齿轮传动系统动态效应的机车动力学模型能够更加真实地模拟变速、变载等极端工况下的机车动力学响应,这为进一步揭示传动系统与车辆系统之间的耦合振动机理打下理论基础。
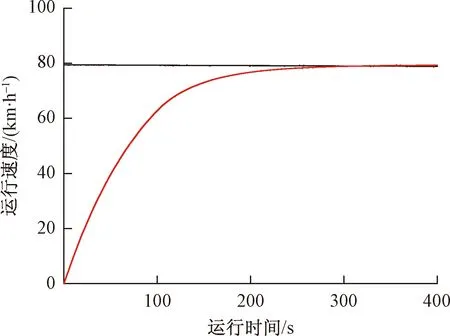
图9 机车运行速度变化曲线
该工况下,机车加速运行至80km/h后进入平稳运行阶段,采用本文建立的重载机车动力学模型仿真获得的4个轮对垂向力时程响应结果如图10和图11所示。由图可知,1、3位轮对减载,2、4位轮对增载,且减载轮对垂向力波动幅度较增载轮对的轮对垂向力更大。
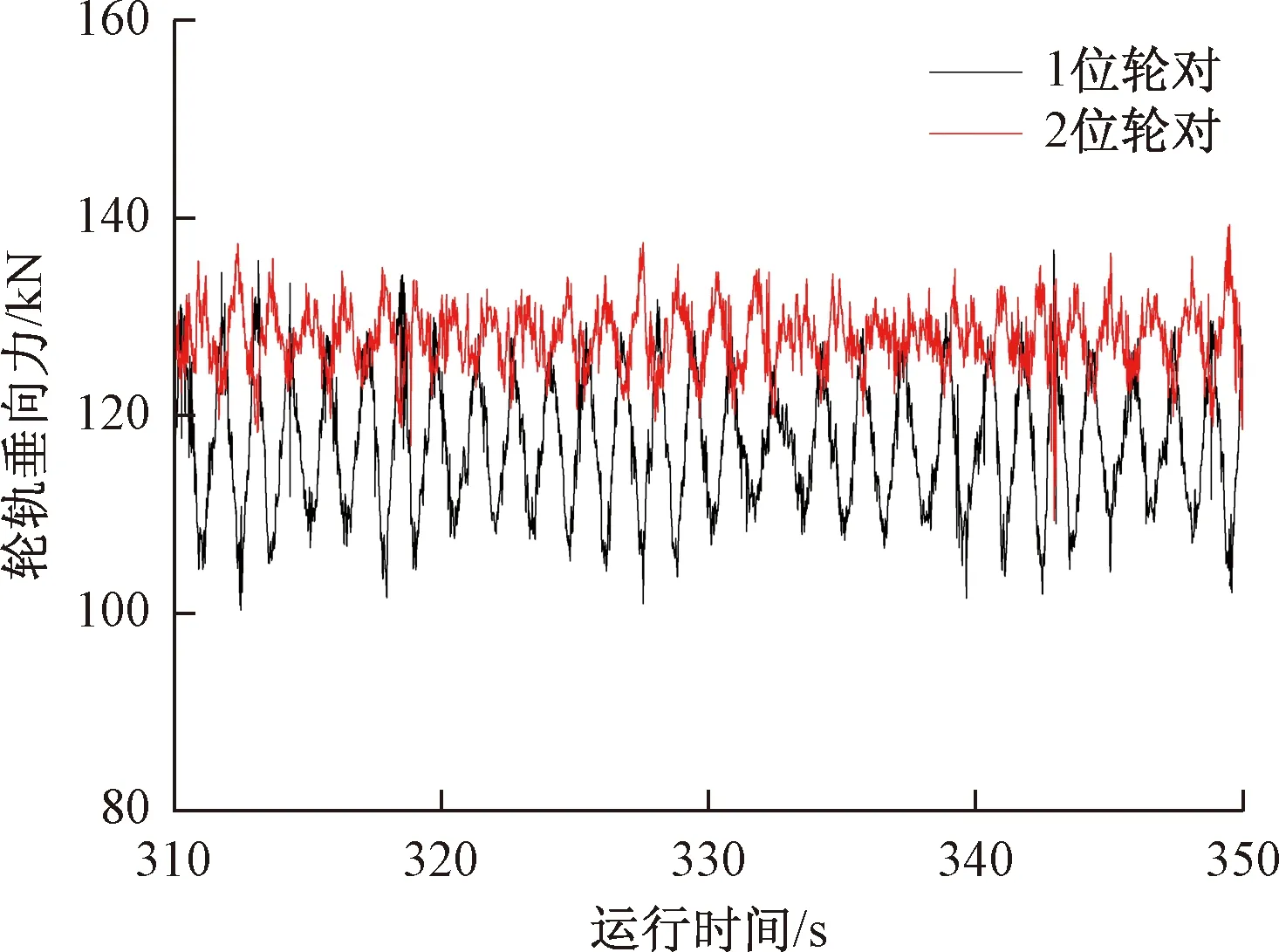
图10 1、2位轮对轮轨垂向力仿真计算时程曲线
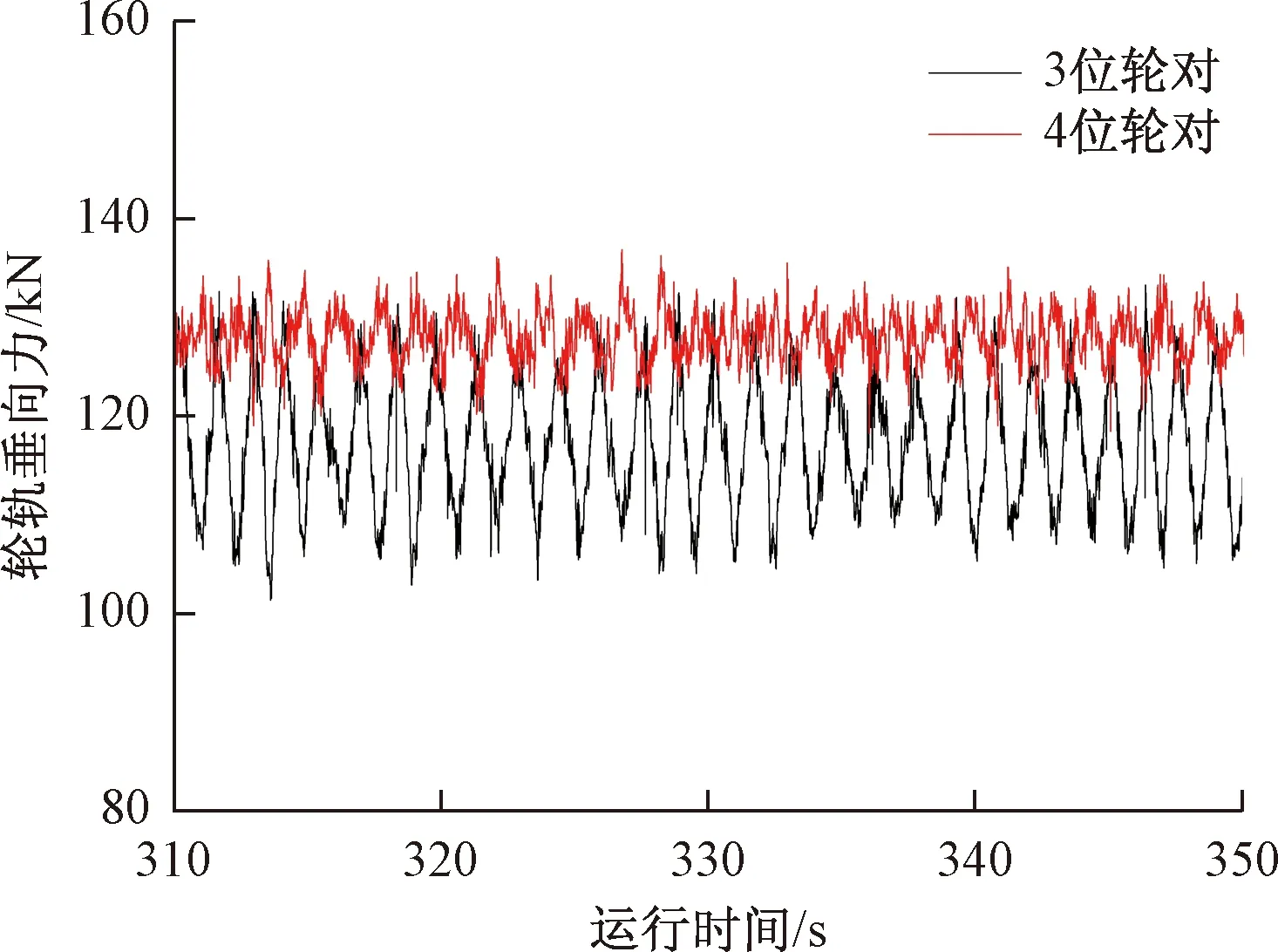
图11 3、4位轮对轮轨垂向力仿真计算时程曲线
类似地,提取图10、图11中轮轨垂向力仿真计算结果的均值,得到4个轮对单侧轮轨垂向力变化规律及对应的轴重转移情况,统计分析结果见表6。

表6 机车轴重转移动力学仿真结果
由表5和表6中的统计结果可知,本文提出的两种方法,即考虑齿轮传动系统动态效应的机车动力学模型法和轴重转移理论解析计算公式法,二者计算获得的轴重转移结果吻合较好,说明了本文建立的两种方法的可靠性。
4 结束语
本文针对某型HX重载电力机车,在传统机车多体动力学模型的基础上,建立了完整的考虑齿轮传动系统动态效应的机车动力学模型,该模型能够更加准确和真实地仿真分析变速变载等复杂工况下的系统主要部件动态响应特性。同时,通过与本文推导获得的轴重转移理论计算公式计算结果进行对比,验证了所建立模型的正确性,结果表明:机车轴重转移理论解析计算公式能够准确地计算机车的轴重转移情况;机车动力学模型与理论解析计算公式计算获得的轴重转移结果吻合较好;考虑齿轮传动系统动态效应后的机车动力学模型能够更真实地仿真分析变速变载等非稳态运行条件下的机车系统动态响应特性。

