含分布式电源的交直流混合配电网潮流分析

郑 眉，陆 翌，许 烽，倪晓军，孟显海

（1.国网浙江省电力有限公司电力科学研究院，杭州 310014；2.浙江大学，杭州 310058；3.南京邮电大学，南京 210023）

0 引言

当前电力系统面对的主要挑战是如何在配电系统中以可持续、安全和有竞争力的方式满足不断增长的对更高质量和可靠性电力的需求。电力电子技术、分布式电源、柔性交流输电系统、能量存储系统以及基于信息和通信技术的高级控制策略方面的重大进步促进了混合交直流配电网的发展[1-2]。而且，混合交直流配电网可控直流输出型分布式电源和直流敏感负荷的显著增长，影响到配电网优化运行状态，产生不平衡负载引起的不对称电流问题等[3]。VSC（电压源换流器）技术的发展，可有效解决混合交直流配电网问题，其具备如下优点：成本低、可减少换流器的数量、对交流系统的依赖性低[4-5]。随着VSC 技术的发展，配电网MTDC（多端直流）的扩展是近年来备受关注的研究方向[6]。

针对VSC-MTDC 已有多方面研究，如稳定性分析、控制策略优化、直流故障定位和保护、动态仿真建模等。文献[7]提出以换流站损耗最小和直流电压偏差最小为目标函数的最优潮流优化方法，并建立了换流站损耗数学模型，可有效减小换流站损耗。文献[8]针对含有PET（电力电子变压器）的交直流混合配电网络，考虑低压交流系统三相负荷不对称的运行模式，提出基于PET 的电压不平衡优化抑制方法，建立了计及换流器损耗的多端口PET 稳态模型，提高了系统运行的经济性和可靠性。文献[9]提出多端互联的交直流配电网分层潮流控制策略，针对交直流配电网的特点，提出高斯-牛顿交直流混合潮流算法，提高了算法的收敛性能，实现了交直流电压的有序控制。文献[10]为防止多端直流输电过程中交流系统故障引起直流母线电压波动进而造成系统失稳，设计了基于无模型自适应技术的VSC。文献[11]运用潮流分析的稳态建模法来解决基于VSCMTDC 的混合交直流配电网系统，对比了连续法和统一法在交流和直流网络方程积分过程中的不同。连序法提出了一种适用于不同VSC 互连配置的综合多端VSC-HVDC 牛顿功率流模型。其中，VSC 被当作复合变压器器件，设计时要考虑它们的电感和电容功率设计极限以及开关损耗和欧姆损耗。

本文分析了VSC 的数学模型，建立了考虑换流器损耗的模型，建模过程依据换流器相电流的多项式函数，而且考虑换流器作为整流器或逆变器时的损耗类型差异。此外，围绕能否有效减少网络损耗问题，研究了在适当位置进行DG（分布式电源）连接时混合交直流配电网络中的换流器损耗对潮流解决方案的影响。通过修改IEEE 33总线AC/MTDC 网络实现了2 种不同的网络场景，以此来验证结果。

1 VSC 换流站模型分析

VSC 换流站由连接交流和直流网络的所有元件组成，基于这些操作特性，分析多端柔性直流配电系统潮流分布。

1.1 VSC 分类

基于MMC（模块化多电平换流器）的VSCMTDC 技术具有降低谐波等优点，可望成为支持VSC-MTDC 网络的新技术[12]。VSC 通常使用绝缘栅双极晶体管，电压波形通过PWM（脉宽调制）与相电抗器、直流电容器和低通滤波器合成，这对于阻止高次谐波流动至关重要。PWM 基于两级或三级VSC 拓扑结构，可实现受控的二级或三级电压输出。

1.2 VSC-MTDC 功率注入建模

在VSC-MTDC 混合交直流配电系统中，VSC换流站组成交直流配电网基本链路[13]。相电抗器和滤波器母线通过变压器连接到AC 网络，并且功率可以在两个方向上流动。当有功功率从AC侧取出并注入到DC 网络时，换流器作为整流器工作；当有功功率从DC 侧反向流到AC 网络时，换流器作为逆变器工作[14]。图1 展示了VSC 换流站的等效电路模型，它包含交流母线、换流变压器、相电抗器、交流滤波器、交流和直流侧换流器模块以及直流母线等不同组件。

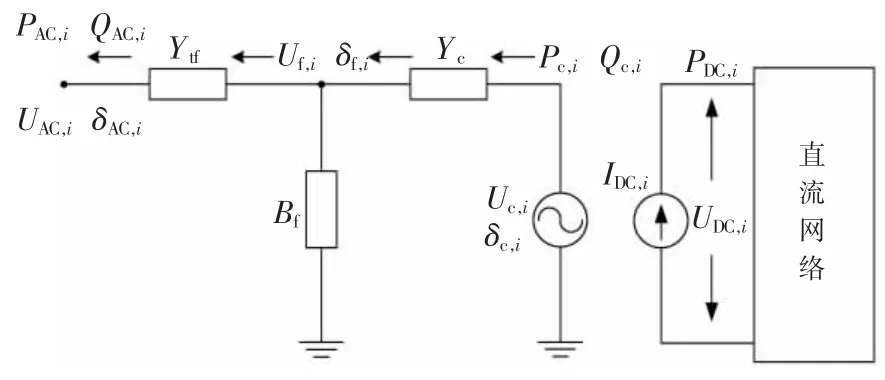
图1 VSC 换流站等效电路模型

根据图1 的等效电路模型，在相电抗器后面的VSC 表示的是可控电压源，，通过复数导纳法求得Yc=Gc+jBc。低通AC 滤波器表示为电纳jBf。换流器变压器接口母线到AC 网络由复数导纳表示为Ytf=Gtf+jBtf。AC 和DC 母线上电网侧电压输出分别表示为和UDC。因此，AC 滤波器总线电压和接口变压器电压可以分别表示为。注入AC 网络的功率为PAC和QAC，从换流器侧流向交流网络的功率是PC和QC，从换流器侧流向直流网络的功率是PDC，根据电压关系可知注入交流电网的有功和无功功率为：

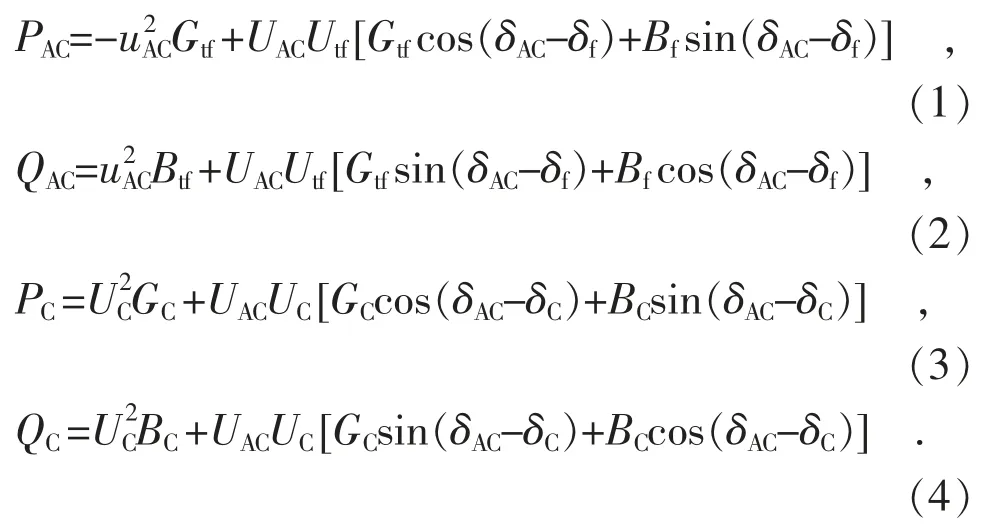
通过上述方程可以相应地实现变压器导纳或滤波器导纳修改。

1.3 换流器损耗建模

考虑到滤波器损耗、相电抗器损耗和变压器阻抗下降这些因素，换流器损耗大小取决于换流器电流Ic的平方，换流器电流大小取决于流经换流器的有功和无功功率，如式（5）所示[15]：

式（6）所示的总换流器损耗Ploss是由常数和可变分量组合而成。恒定损耗是与器件的关断状态相关联的电路损耗，而线性损耗是与电流状态相关的开关损耗，可变损耗与生成的热损耗和反向恢复损耗相关联。

式中：A，B和C代表单位损耗系数，并取决于VSC 损耗的测试数据。

对于交流系统来说，VSC 独立控制有功功率和无功功率来实现多种控制模式，可以通过以下不同方式表示有功功率和无功功率控制模式。

（1）恒定PAC控制模式：换流器控制其恒定的有功功率注入PAC，并注入交流电网。

（2）恒定UDC控制模式：换流器控制其恒定的直流母线电压UDC，无论换流器的有功功率是否注入PAC。

（3）恒定QAC控制模式：换流器控制其恒定无功功率注入QAC，并注入交流电网。

（4）恒定UAC控制模式：换流器通过调节无功功率注入QAC来控制其恒定的交流总线电压UAC。

2 混合交直流配电网连续潮流算法

2.1 连续潮流算法流程

连续潮流算法包含估计、校正、参数化和步长控制等基本步骤，连续潮流计算是混合交直流配电网分析的重要工具，对提高计算可靠性和计算效率有重大意义，有助于大型电力系统的电压稳定性分析。混合交直流配电网连续潮流算法运用在与VSC 结合的混合交直流配电系统上，对于分析含有分布式电源的交直流配电网中的网络损耗是非常重要的，通过采用定步长和估计初值的基本策略，运用N-R（牛顿-拉夫逊）法来求解算法中的非线性潮流方程组，以此来分析网络中换流器的建模方式、网络损耗建模方式以及网络中换流器的数量。该算法还可以运用在具有多个交直流网络互连的系统，以及那些没有交流电网连接的直流母线，能够满足大型电力系统工程计算的需要，有助于分析电力系统中电压崩溃和安全性分析。图2 展示了连续潮流算法的流程。

图2 混合交直流配电网连续潮流算法流程

2.2 连续潮流算法步骤

第一步：数据输入和单位转换。首先将所有换流器数据和交直流网络数据转换为单位标幺值。

第二步：确定交流网络的换流器的有功功率注入。假设直流网络和换流器是无损的，为实现迭代计算，采用式（7）计算得到的直流网络功率参考负值来估计交流网络换流器有功功率注入的初始值。

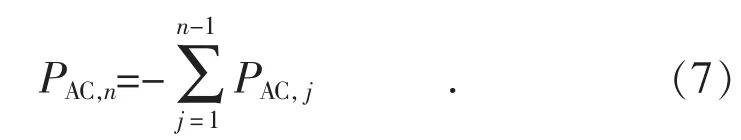
有源功率注入交流网络的矢量表示可以为：

式中：n表示MTDC 网络中连接的换流器总数。第n个换流器与直流松弛节点连接，第n-1 个换流器总线则处于恒定有功功率控制之下，假设剩余的总线未连接到交流网络。

第三步：确定网络类型。如果是交流网络，执行第四步；如果是直流网络，执行第六步。

第四步：交流网络潮流计算。当为交流网络潮流计算时，所有换流器和直流网络数据都被认为是恒定的，交流网络潮流计算的有功和无功功率方程可写成：

式中：m为直流网络母线的总数。换流器功率注入PAC，i和QAC，i作为负载包括在功率失配矢量ΔP和ΔQ中。失配向量可以表示为：

式中：分别代表连接交流网络总线的有功和无功功率发生器；分别代表交流网络总线上连接的负载消耗的有功和无功功率；PAC，i和QAC，i分别代表通过VSC 注入的有功功率和无功功率；Pi（u，δ）和Qi（u，δ）分别表示由交流潮流计算得到的交流网络母线的有功和无功功率。

利用N-R 潮流算法来求解非线性潮流方程组[16]，由式（13）确定所有交流母线的电压和相位角。

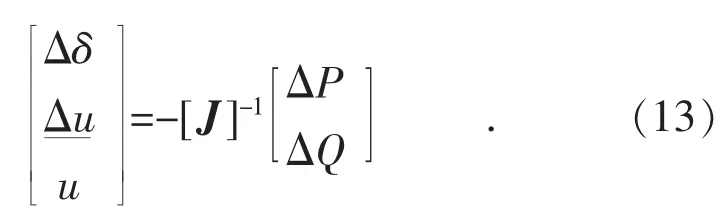
第五步：计算换流器功率和损耗。通过交流网络潮流计算后，交流母线电压UAC，i，向交流网络侧注入的所有换流器有功功率PAC，i和无功功率QAC，i及损耗Ploss，运用式（1）—（4）和式（6）计算。

第六步：直流网络潮流计算。将功率PDC，i注入到直流网络，使换流器与直流母线相连接，通过如下方程计算：

式中：Pc，i表示注入换流器侧的复合功率的有功部分；Ploss，i表示注入换流器侧的有功功率损耗。

直流网络潮流计算类似于传统的交流网络潮流计算，不考虑无功功率和线路电抗，因为它在直流网络中不起任何作用。直流网络的电导矩阵GDC可以表示为：

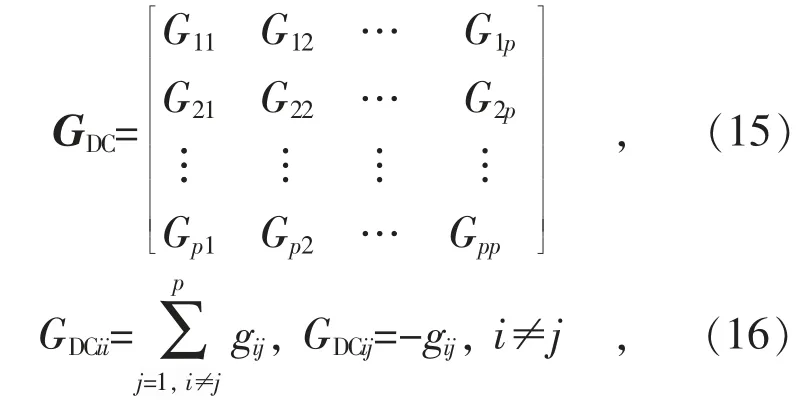
式中：p表示直流网络母线的总数。

注入直流网络的电流可以写成：

式 中：代表直流电压；代表直流电流。

直流网络上的有功功率注入PDC，i计算如下：

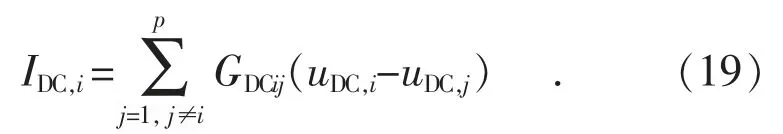
采用N-R 算法计算直流母线电压：

第七步：确定网络类型。如果是交流系统，执行第八步；如果网络不是交流系统，执行第四步；如果是直流系统，则执行第五步。

第八步：当计算出交直流系统中的所有未知数之后，另外通过迭代计算在换流器侧注入交流系统的有功功率Pc，n，它取决于直流松弛节点功率PDC，n和换流器损耗Ploss，n，如式（21）所示：

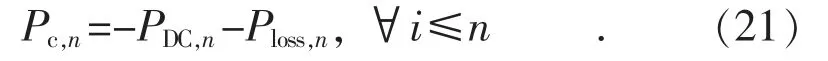
迭代的时候，假设直流网络侧电压UAC和注入到交流网络的无功功率QAC是恒定的。

第九步：收敛标准。交直流潮流算法的收敛标准由换流器侧注入交流网络的有功功率的差值设定，如式（22）所示：

式中：k 和ε 分别表示潮流迭代次数和收敛检查的容差值。

如果结果收敛，则计算结束，否则返回第二步，更新当前迭代的配电网的数据。

3 混合交直流配电网模型

3.1 混合交直流配电网拓扑结构

混合交直流配电系统中的拓扑结构如图3 和图4 所示[17]，修改后的拓扑建模方法对配电网的配置和拓扑没有任何限制，并且该设计还可以使不同类型的DER（分布式能源）和混合交直流配电系统互连。

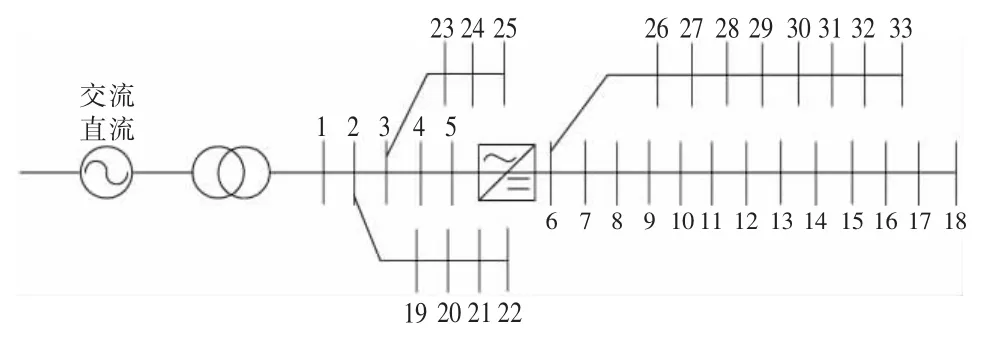
图3 混合交直流配电网模型-拓扑1

图4 混合交直流配电网模型-拓扑2

基准功率、基准交流电压值和基准直流电压分别为100 MVA，12.66 kV 和1.5 kV。电压和功率数据都以标幺值（p.u.）表示。所有换流变压器的电阻和漏抗均取为（0.001 5+j0.112 1）p.u.，滤波器电纳为j0.04 5 p.u.，电抗器阻抗为（0.000 1+j0.164 3）p.u.。

3.2 混合交直流配电网中分布式能源配置

混合交直流配电网模型-拓扑1 如图3 所示。在混合交直流配电网中对拓扑进行修改，在母线5 和母线6 之间增加了VSC 换流器。在这种直流母线占主导地位的拓扑结构中，交流与直流母线的比率为1:2。而且在该拓扑结构中，将交流母线1 作为交流松弛母线，交流电压幅值为1.05 p.u.，相位角为零。在直流网络中，将直流母线6 作为直流松弛母线，直流电压幅值为1.05 p.u.，其余交流母线电压幅值为1 p.u.，相位为零，直流母线电压幅值为1.0 p.u.，并作为平启动值。

混合交直流配电网模型-拓扑2 如图4 所示。在这种拓扑结构中，在网络的始端和母线5、母线6 之间增加了VSC 换流器。不同于拓扑1，它是交流母线占主导地位，交流与直流母线的比例为2:1。在该拓扑中，将交流电压幅值为1.05 p.u.的交流松弛母线作为交流母线6，将直流电压幅值为1.05 p.u.的直流松弛母线作为直流母线1。仿真中，其余交流母线的电压幅值均为1.0 p.u.，相位为零，而直流母线电压幅值为1.0 p.u.。

表1 和表2 所示为3 种情形中对配电网中分布式能源的配置。

场景1——传统的交流配电网：所有的分布式能源都在交流网络侧连接，并且输出只有交流。

场景2——混合交直流配电网：所有的分布式能源都在直流网络侧连接，并且输出只有直流。

场景3——交直流混合配电网：分布式能源连接在交流网络和直流网络之间，具体取决于分布式能源的输出类型。其中，分布式能源和负荷被建模为常数，而不考虑分布式能源的变化性质，其输出取决于许多自然因素。

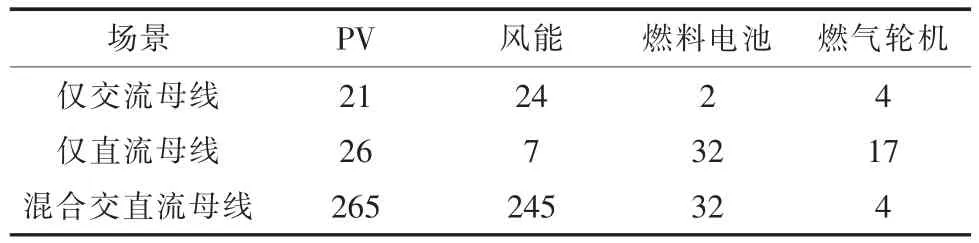
表1 拓扑1 中的分布式能源

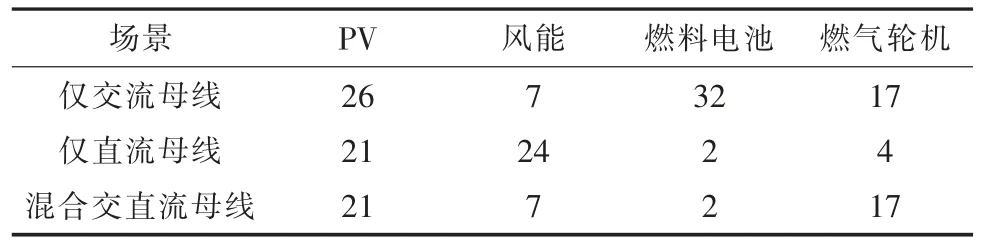
表2 拓扑2 中的分布式能源

4 潮流仿真与结果

本节介绍上述拓扑结构的潮流结果。所有仿真都采用10-4p.u.的收敛容差。

4.1 拓扑1 潮流结果

在拓扑中，所有的场景都在4 次迭代中收敛。拓扑的潮流解决方案详见表3—表5。表3 中的仿真结果展示了在给定场景2 和场景3 下的电压曲线有所改善。

表3 拓扑中的潮流仿真结果 p.u.

由表4 和表5 可知：在给定场景2 和场景3下，在直流网络上连接的分布式能源使得从交流网络到直流网络注入功率减少，导致配电网中换流器数量和网络损耗减少；如果使用集成的分布式能源，那么换流器或逆变器的损耗会减少，则情景3 中的总损耗也会有所降低。

图5 展示了场景3 下的研究结果。考虑到在直流网络上连接的分布式能源的增加导致整体网络损耗的减少，而假设在交流网络中的分布式能源恒定，交流和直流网络的负载也是恒定的。

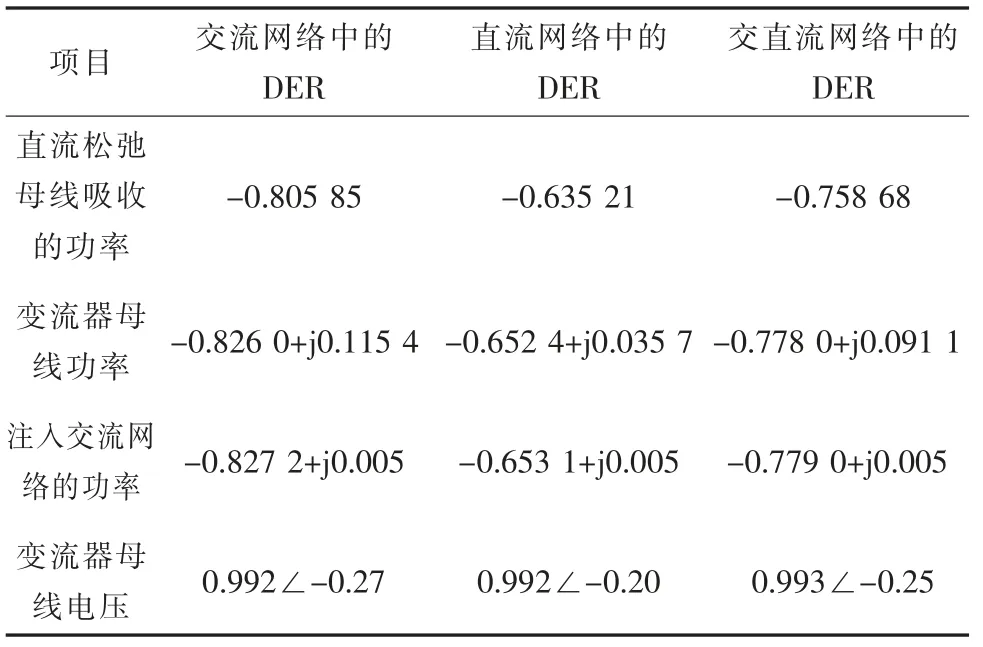
表4 多端柔性直流配电系统潮流 p.u.

表5 多端柔性直流配电系统拓扑损耗 p.u.

图5 DER 容量（DC 输出）的增加引起网络损耗变化

4.2 拓扑2 潮流结果

在拓扑2 中，所有的场景都在2 次迭代中收敛。表6—表8 展示了拓扑2 的潮流结果，可以看出：对于所有给定的情况，电压分布都会有所改善，并且拓扑2 中的压降有所改善（如表6 所示）；在场景2 和场景3 中，与交流线路损耗相比，从交流网络到直流网络的总直流线路损耗为最小（如表7 所示）。

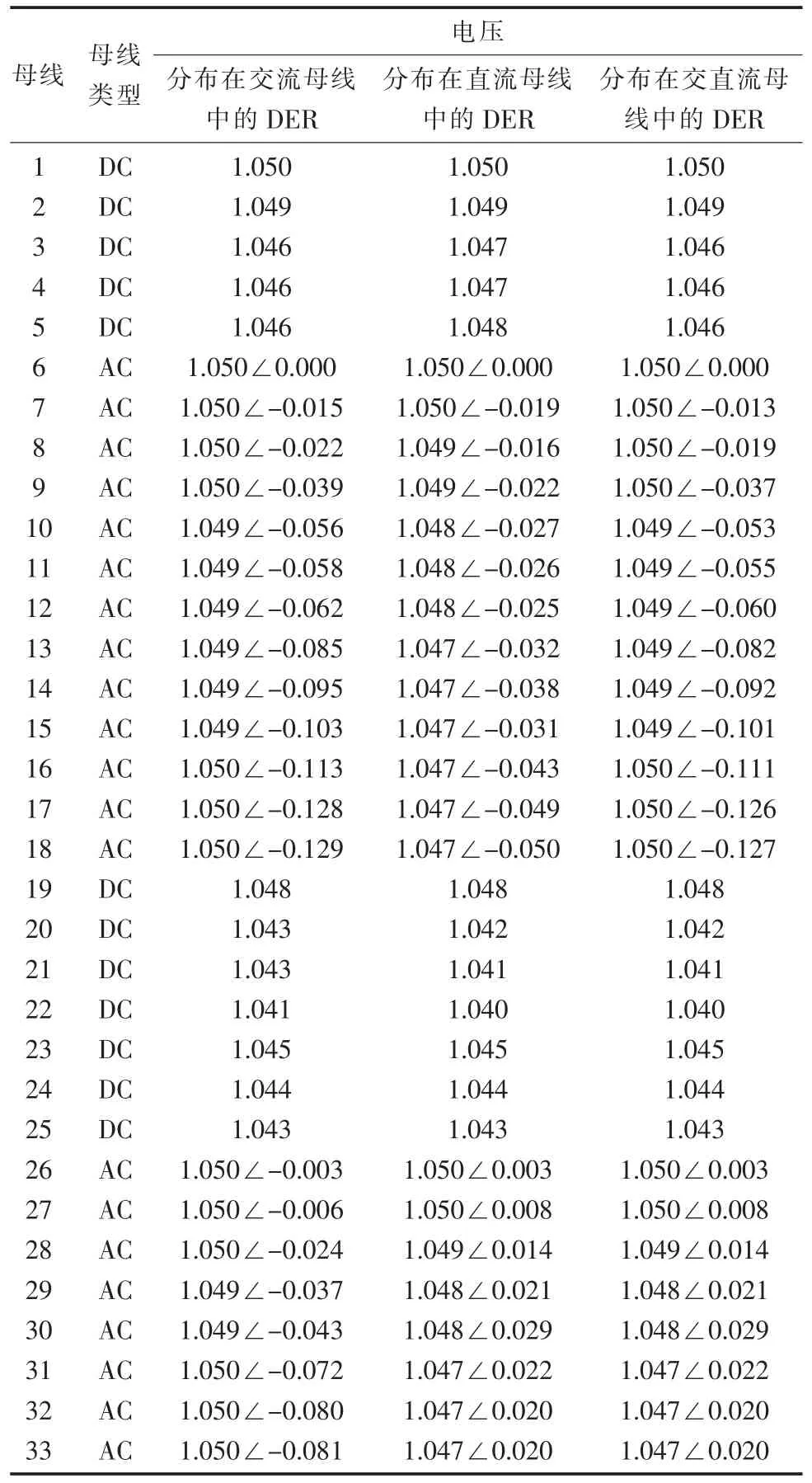
表6 拓扑2 中的负载电压仿真结果 p.u.

对于给定的拓扑结构，表8 中的结果表明，由于使用集成DER，与场景1 和场景2 相比，场景3 中的换流器或者逆变器总损耗最小。结果与不使用集成DER 时换流器或逆变器的损耗做了比较。

针对该拓扑，在交流网络和直流网络中增加连接的DER 容量，并且在场景3 中保持交流和直流网络负载恒定。图6 表明，随着交流发电量的增加，网络损耗会增加。

表7 混合交直流配电系统拓扑2 潮流分布 p.u.

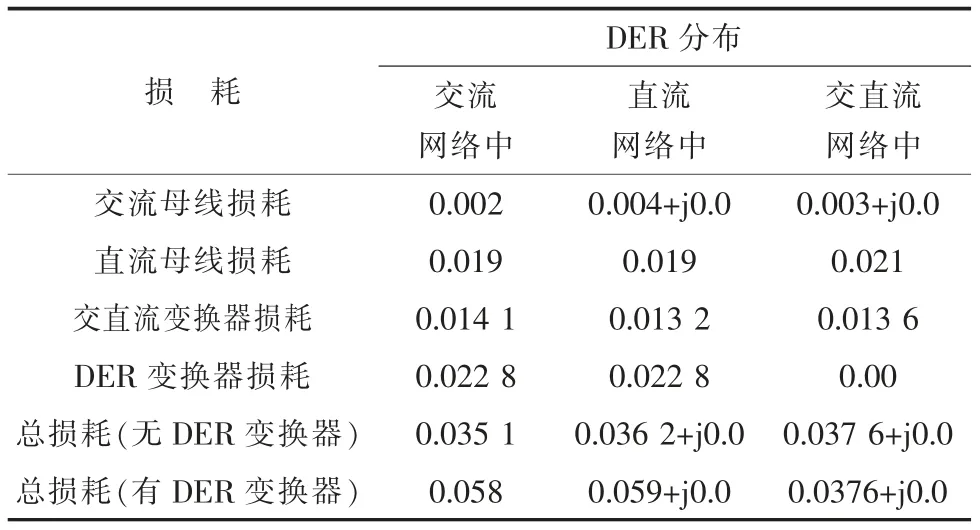
表8 混合交直流配电系统拓扑2 损耗 p.u.

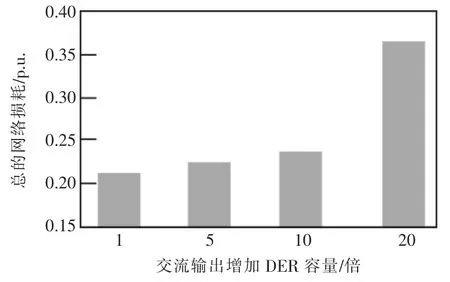
图6 DER 容量（AC 输出）的增加引起网络损耗变化

对比表5 和表8 中2 种拓扑下的损耗可知，与场景1 和场景2 相比，场景3 由于转换阶段的数量较少，使得整体系统损失减少。图7 和表9给出了在场景3 下2 种拓扑结构与影响混合交直流配电网负载流的一些其他附加因素的比较，可以得出结论：合理的DER 分布能够使混合交直流配电系统的网络功率传输和损耗减少；在基于VSC-MTDC 网络中的换流器损耗是不可忽略的，并且在混合交直流配电网的实施和规划中起着重要作用。

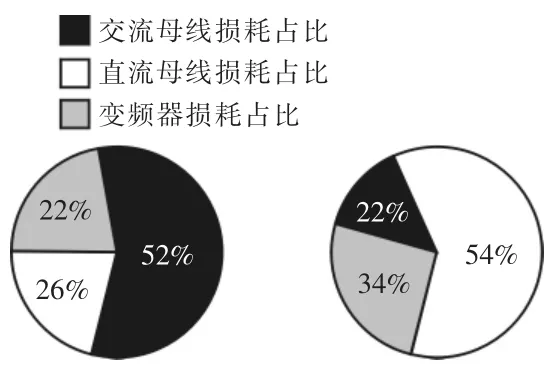
图7 场景3 中拓扑1 和拓扑2 的损耗比较

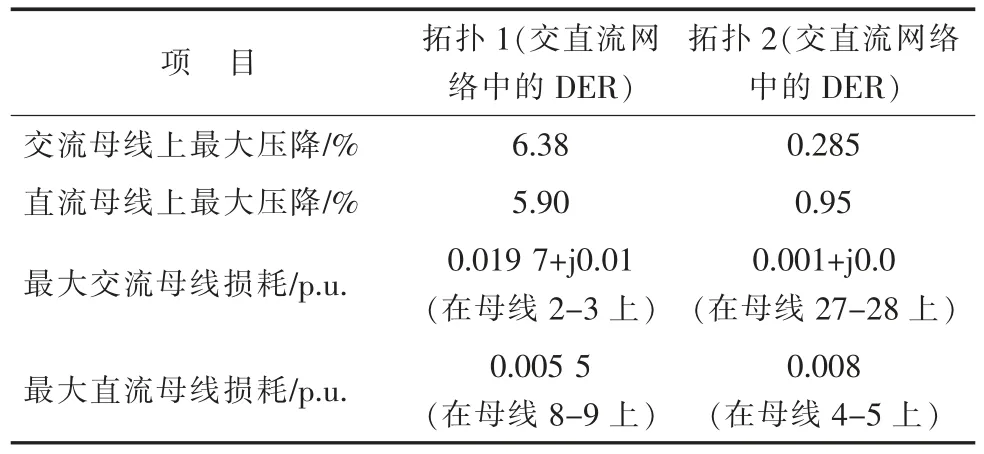
表9 场景3 中拓扑1 和拓扑2 的结果比较

5 结语

本文介绍了混合交直流配电网潮流计算NR 算法的设计和实现，包括损耗建模和不同控制模式的VSC 建模，分析了混合交直流配电网所构建的2 个示例系统中换流器和网络损耗的影响。研究结果表明：考虑输出类型时网络中合理的DER 分布对于减少网络中的损耗是非常重要的；潮流保护解决方案取决于换流器的建模方式、网络损耗建模方式以及网络中换流器的数量；正确的换流器损耗建模很重要，因为在交流MTDC网络中是不可能忽略换流器损耗的，否则可能会导致不同的潮流值和不完整的整体网络损耗评定。就实现效果而言，换流器损耗和交流或直流网络分支的数量应该比较容易解决，这样也会便于将来规划和扩展MTDC 网络。